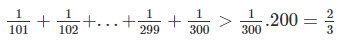Tính chất cơ bản của phép nhân phân số
Bài 93 (Sách bài tập - tập 2 - trang 27)
Khi giặt, vải bị co đi \(\dfrac{1}{16}\) theo chiều dài và \(\dfrac{1}{18}\) theo chiều rộng. Hỏi cần phải mua bao nhiêu mét vải khổ 80cm để sau khi giặt có \(17m^2\) ?
Hướng dẫn giải
Sau khi giặt , cứ 1m vải theo chiều dài sẽ còn lại :
\(\dfrac{15}{16}.\dfrac{17}{18}.\dfrac{8}{10}\) = \(\dfrac{17}{24}\)(m2 ) vải ,
Vì vậy ,ta càn phải mua 24m để sau khi giặt có 17m2 vải
Bài 11.7* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Tính giá trị của biểu thức :
\(M=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+....+\dfrac{1}{10.11.12}\)
Hướng dẫn giải
Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)
Bài 11.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Chứng tỏ rằng :
\(\dfrac{1}{101}+\dfrac{1}{102}+.....+\dfrac{1}{299}+\dfrac{1}{300}>\dfrac{2}{3}\)
Hướng dẫn giải
Bài 11.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Giá trị của biểu thức :
\(A=\dfrac{-3}{5}.\dfrac{1}{9}+\dfrac{2}{15}.\left(-7\right)+\dfrac{12}{-7}.\dfrac{-7}{6}\) là :
(A) -2 (B) 2 (C) -1 (D) 1
Hãy chọn đáp án đúng ?
Hướng dẫn giải
(D) 1
Bài 92 (Sách bài tập - tập 2 - trang 27)
Lúc 6 giò 50 phút, bạn Việt đi xe đạp từ A đến B với vận tốc 15 km/h. Lúc 7 giờ 10 phút, bạn Nam đi xe đạp từ B đến A với vận tốc 12km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB ?
Hướng dẫn giải
Việt đi quãng đường AC trong số thời gian là:
7 giờ 30 phút - 6 giờ 50 phút = 40 phút = \(\dfrac{2}{3}\) (giờ)
Nam đi quãng đường BC trong số thời gian là:
7 giờ 30 phút - 7 giờ 10 phút = 20 phút = \(\dfrac{1}{3}\) (giờ)
Quãng đường AC dài số ki-lô-mét là:
\(15 . \dfrac{2}{3} = \dfrac{30}{3}=10 (km)\)
Quãng đường BC dài số ki-lô-mét là:
\(12.\dfrac{1}{3}=\dfrac{12}{3}=4(km)\)
\(\Rightarrow\) Quãng đường AB dài số ki-lô-mét là:
10 + 4 = 14(km)
Vậy quãng đường AB dài 14 km
Bài 11.6* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Chứng tỏ rằng :
\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+....+\dfrac{1}{17}< 2\)
Hướng dẫn giải
Ta có : \(\dfrac{1}{5}=\dfrac{1}{5}\), \(\dfrac{1}{6}< \dfrac{1}{5}\), \(\dfrac{1}{7}< \dfrac{1}{5}\),...,\(\dfrac{1}{9}< \dfrac{1}{5}\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{9}< \dfrac{1}{5}\cdot5=1\)
\(\dfrac{1}{10}< \dfrac{1}{8},\dfrac{1}{11}< \dfrac{1}{8},...,\dfrac{1}{17}< \dfrac{1}{8}\)
Vậy \(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}< \dfrac{1}{8}\cdot8=1\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{17}< 1+1=2\)
Chúc các bạn học tốt
Bài 11.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{5}\) (B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
(C) \(\dfrac{1}{3}.\dfrac{1}{5}+\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}+\dfrac{1}{2}\right)\) (D) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\left(\dfrac{1}{3}.\dfrac{1}{2}\right)\)
Hãy chọn đáp án đúng ?
Hướng dẫn giải
Trong các đẳng thức trên ,đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
Bài 11.5* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Tính tích \(A=\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}....\dfrac{899}{900}\)
Hướng dẫn giải
\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\\ =\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\\ =\dfrac{1\cdot2\cdot3\cdot...\cdot29}{2\cdot3\cdot4\cdot...\cdot30}\cdot\dfrac{3\cdot4\cdot5\cdot...\cdot31}{2\cdot3\cdot4\cdot...\cdot30}\\ =\dfrac{1}{30}\cdot\dfrac{31}{2}\\ =\dfrac{31}{60}\)
Vậy ...
Bài 94 (Sách bài tập - tập 2 - trang 27)
Tính giá trị các biểu thức :
\(A=\dfrac{1^2}{1.2}.\dfrac{2^2}{2.3}.\dfrac{3^2}{3.4}.\dfrac{4^2}{4.5}\) \(B=\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}.\dfrac{5^2}{4.6}\)
Hướng dẫn giải
a) A = \(\dfrac{1^2}{1.2}.\dfrac{2^2}{2.3}.\dfrac{3^2}{3.4}.\dfrac{4^2}{4.5}\)
A = \(\dfrac{1.1}{1.2}.\dfrac{2.2}{2.3}.\dfrac{3.3}{3.4}.\dfrac{4.4}{4.5}\)
A = \(\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.\dfrac{4}{5}\)= \(\dfrac{1}{5}\)
b) B = \(\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}.\dfrac{5^2}{4.6}\)
B = \(\dfrac{2.3.4.5}{1.2.3.4}.\dfrac{2.3.4.5}{3.4.5.6}\)= \(\dfrac{5}{3}\)
Bài 91 (Sách bài tập - tập 2 - trang 27)
Áp dụng các tính chất của phép nhân phân số để tính nhanh :
\(M=\dfrac{8}{3}.\dfrac{2}{5}.\dfrac{3}{8}.10.\dfrac{19}{92}\)
\(N=\dfrac{5}{7}.\dfrac{5}{11}+\dfrac{5}{7}.\dfrac{2}{11}-\dfrac{5}{7}.\dfrac{14}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right).\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
Hướng dẫn giải
\(M=\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\\ =\dfrac{8\cdot2\cdot3\cdot10\cdot19}{3\cdot5\cdot8\cdot92}\\ =\dfrac{8\cdot2\cdot3\cdot2\cdot5\cdot19}{3\cdot5\cdot8\cdot2\cdot2\cdot23}\\ =\dfrac{19}{23}\)
\(N=\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\\ =\dfrac{5}{7}\cdot\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}\cdot\left(-\dfrac{7}{11}\right)\\ =-\dfrac{5}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot0\\ =0\)
Bài 95* (Sách bài tập - tập 2 - trang 28)
Tính nhanh :
\(M=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+....+\dfrac{2}{97.99}\)
Hướng dẫn giải
\(M=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}\)
\(M=2.(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99})\)
\(M=2.\left(\dfrac{1}{3}-\dfrac{1}{99}\right)\)
\(M=2.\dfrac{32}{99}\)
\(M=\dfrac{64}{99}\)
Bài 89 (Sách bài tập - tập 2 - trang 27)
Điền các số thích hợp vào bảng sau :
| a | \(\dfrac{-3}{4}\) | \(\dfrac{5}{9}\) | \(\dfrac{-7}{25}\) | \(\dfrac{4}{7}\) | \(\dfrac{-4}{19}\) | \(\dfrac{-18}{15}\) | \(\dfrac{50}{21}\) | ||
| b | \(\dfrac{4}{7}\) | \(\dfrac{-18}{15}\) | \(\dfrac{50}{21}\) | \(\dfrac{-3}{7}\) | \(\dfrac{-3}{4}\) | \(\dfrac{5}{9}\) | \(\dfrac{6}{13}\) | \(\dfrac{-7}{25}\) | |
| a.b | \(1\) | \(\dfrac{-4}{19}\) | \(0\) |
Hướng dẫn giải
Bài 90 (Sách bài tập - tập 2 - trang 27)
Tính nhanh giá trị các biểu thức sau :
\(A=\dfrac{6}{7}+\dfrac{1}{7}.\dfrac{2}{7}+\dfrac{1}{7}.\dfrac{5}{7}\) \(B=\dfrac{4}{9}.\dfrac{13}{3}-\dfrac{4}{3}.\dfrac{40}{9}\)
Hướng dẫn giải
\(A=\dfrac{6}{7}+\dfrac{1}{7}.\dfrac{2}{7}+\dfrac{1}{7}.\dfrac{5}{7}.\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}\left(\dfrac{2}{7}+\dfrac{5}{7}\right).\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}.1.\)
\(A=\dfrac{6}{7}+\dfrac{1}{7}=1.\)
Vậy \(A=1.\)
\(B=\dfrac{40}{9}.\dfrac{13}{3}-\dfrac{4}{3}.\dfrac{40}{9}.\)
\(B=\dfrac{4}{9}.\dfrac{13}{3}-\dfrac{4}{9}.\dfrac{40}{3}.\)
\(B=\dfrac{4}{9}\left(\dfrac{13}{3}-\dfrac{40}{3}\right).\)
\(B=\dfrac{4}{9}.\left(-9\right).\)
\(B=-4.\)
Vậy \(B=-4.\)
Bài 11.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Tính tích \(P=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{99}\right)\)
Hướng dẫn giải
\(P=\left(1-\dfrac{1}{2}\right)\cdot\left(1-\dfrac{1}{3}\right)\cdot\left(1-\dfrac{1}{4}\right)\cdot...\cdot\left(1-\dfrac{1}{99}\right)\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{98}{99}\\ =\dfrac{1\cdot2\cdot3\cdot...\cdot98}{2\cdot3\cdot4\cdot...\cdot99}\\ =\dfrac{1}{99}\\ Vậy....\)