Ôn tập chương Hình lăng trụ đứng. Hình chóp đều.

Lý thuyết

Bài 79 (Sách bài tập - tập 2 - trang 155)

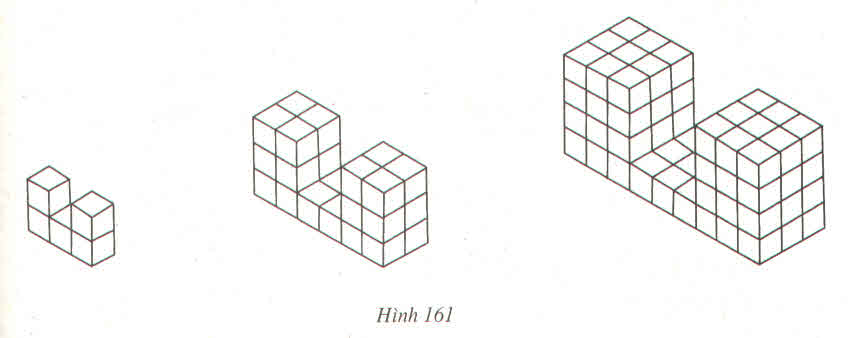
Hãy quan sát ba hình dưới đây (h.161), trong đó các hình lập phương đơn vị được xếp theo dạng hình chữ U

Số các hình lập phương đã xếp tăng lên theo quy luật :

                    5 hình -> 28 hình -> 81 hình

Nếu theo quy luật này thì có bao nhiêu hình lập phương đơn vị ở hình thứ 10 ?

 

 

Hướng dẫn giải

Số hình lập phương ở hình 1: 1.3+1.1.2=5 (khối)

Số hình lập phương ở hình 2:2².3+2².2.2=28 (khối)

Số hình lập phương ở hình 3:3².3+3².3.2=81 (khối)

\(\Rightarrow\)Công tức tính:

Số hình lập phương ở hình x: x².3+x².x.2 (khối)

Số hình lập phương ở hình 10 là:10².3+10².10.2=2300 (khối)

Bài IV.2* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 158)

Một con kiến đang ở vị trí M là trung điểm cạnh A'D' của một chiếc hộp hình lập phương ABCD.A'B'C'D' (h.bs.16). Con kiến muốn bò qua sau mặt của chiếc hộp rồi quay trở về M. Tìm đường đi ngắn nhất của con kiến ?

Hướng dẫn giải

Trải 6 mặt của hình lập phương ABCD.A'B'C'D' . Để đi đường ngắn nhất từ M đến M' ( M' chính là trung điểm của A'D' trên mặt khai triển ) thì con kiến cần bò theo đoạn thẳng MM' . Trên chiếc hộp , đường đi ngắn nhất của con kiến là đường MNPQKZM ( dễ thấy N , P ,Q , K , Z lần lượt là trung điểm của DD' , CD , BC , BB' , A'B' )

Bài 89 (Sách bài tập - tập 2 - trang 157)

Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào ? (không được cắt, xẻ.....)

Hướng dẫn giải

Gọi viên gạch là hình hộp chữ nhật ABCD.A₁B₁C₁D₁. Để đo đường chéo AC ta làm như sau : trên tia đối của tia CC₁ ta lấy điểm C₂ sao cho CC₁ = CC₂

Dùng thước chia vạch AC₂ chính là độ dài đường chéo AC₁

====> Nếu thấy đúng thì nhớ bấm đúng cho mềnh nhé

Bài IV.5 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 159)

Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hay đáy, tính chiều cao của hình chóp cụt đều.

Hướng dẫn giải

Xét hình chóp cụt đều ABCD.AB'C'D'

Gọi M ,M' thứ tự là trung điểm của BC , B'C' . Khi đó MM' là đường cao của hình thang cân BCC'B' . Do đó diện tích xung quanh của hình chóp cụt đều là :

\(S_{xq}=4.\dfrac{a+b}{2}.MM'=\left(2a+2b\right).MM'\)

Từ giả thiết , ta có :

\(\left(2a+2b\right).MM'=a^2+b^2hayMM'=\dfrac{a^2+b^2}{2\left(a+b\right)}\left(1\right)\)

Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O') . Trong mặt phẳng (OMM'O') , kẻ MH \(\perp\) O'M' . Khi đó : \(HM'=O'M'-O'H=\dfrac{b-a}{2}\)

Trong tam giác vuông MHM' ta có :

\(MM'^2=MH^2+HM'^2=h^2+\left(\dfrac{b-a}{2}\right)^2\left(2\right)\)

Từ (1) và (2) suy ra :

\(h^2+\left(\dfrac{b-a}{2}\right)^2=\dfrac{\left(a^2+b^2\right)^2}{4\left(a+b\right)^2}\)

\(\Rightarrow h^2=\dfrac{\left(a^2+b^2\right)^2-\left(b^2-a^2\right)^2}{4\left(a+b\right)^2}=\dfrac{a^2b^2}{\left(a+b\right)^2}\)

Vậy \(h=\dfrac{ab}{a+b}\)

Bài 85 (Sách bài tập - tập 2 - trang 156)

Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 10 cm, chiều cao hình chóp là 12 cm. Tính :

a) Diện tích toàn phần của hình chóp

b) Thể tích hình chóp

Hướng dẫn giải

Bài 80 (Sách bài tập - tập 2 - trang 156)

Hãy tìm diện tích mặt ngoài theo các kích thước cho ở hình 162. Biết rằng hình a) gồm một hình chóp đều và một hình hộp chữ nhật, hình b) gồm hai hình chóp đều 

Hướng dẫn giải

Bài 82 (Sách bài tập - tập 2 - trang 156)

Cho biết hộp có dạng hình hộp chữ nhật, độ dài đường chéo là 50cm. Hãy tìm các kích thước của hai hình hộp như vậy ?

(Hướng dẫn : Đây là một bài toán mở, hãy chọn hai trong ba kích thước của hình hộp có thể chấp nhận được, từ đó tính kích thước còn lại)

Hướng dẫn giải

\(a=20cm,b=24cm\) khi đó

\(a^2+b^2+c^2=50^2hay400+576+c^2=2500\)

suy ra \(c^2=1524\) .Vậy \(c\approx39\left(cm\right)\)

Bài 78 (Sách bài tập - tập 2 - trang 155)

Độ dài đường chéo \(AC_1\) (h.160) của một hình lập phương là \(\sqrt{12}\)

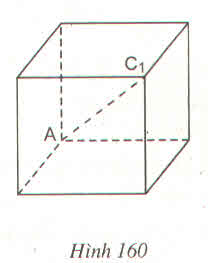
a) Độ dài mỗi cạnh là bao nhiêu ?

b) Tính diện tích toàn phần và thể tích của hình lập phương

Hướng dẫn giải

\(a,\)Độ dài mỗi cạnh của hình lập phương là : 2 (đơn vị chiều dài )

\(b,\)_Thể tích hình lập phương : 8 (đơn vị thể tích )

_Diện tích toàn phần gần bằng 24 (đơn vị diện tích )

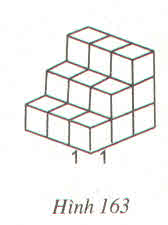
Bài 81 (Sách bài tập - tập 2 - trang 156)

Số hình lập phương đơn vị ở hình dưới đây (h.163) là bao nhiêu (mỗi hình lập phương nhỏ là một hình lập phương đơn vị ) ?

Hướng dẫn giải

hình trên có 18 hình lập phương đơn vị

Bài 77 (Sách bài tập - tập 2 - trang 155)

Thùng của một xe tải có dạng một hình lăng trụ đứng (h.159) các kích thước cho ở trên hình 

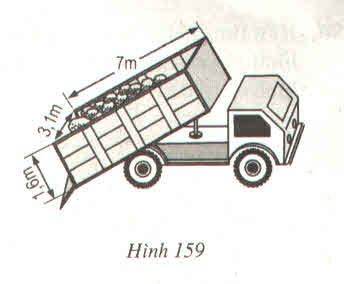
a) Tính thể tích của thùng chứa

b) Nếu \(1m^3\) cát nặng 1,6 tấn và xe chở đến \(\dfrac{3}{4}\) trọng tải của nó thì sức nặng của cát lúc đó là bao nhiên ?

c) Khi cát được san phẳng trở đầy thì phần diện tích của nó bên trong thùng xe là bao nhiêu ?

Hướng dẫn giải

\(a,\) Thùng chứa có dạng một lăng trụ đứng

V= 1,6.3,1.7=34,72 (m³)

\(b,\) Cát nặng :

\(34,72.\dfrac{3}{4}.1,6=41,664\) (tấn)

Bài 75 (Sách bài tập - tập 2 - trang 154)

"Bồn" đựng nước có dạng một hình lăng trụ đứng (h.157) các kích thước cho trên hình 

a) Tính diện tích bề mặt của bồn (không tính nắp)

b) Tính thể tích của bồn

c) Khi bồn đầy ắp nước thì nó chứa được bao nhiêu lít ?

d) Lượng sơn cần thiết để sơn cả mặt trong lẫn mặt ngoài của bồn là bao nhiêu (một lít sơn phủ được \(16m^2\) )

e) Một vòi bơm với công suất 125 lít/phút, để bơm một lượng nước vào bồn lên đến độ cao cách thành bồn là 1,05 mét thì phải mất bao lâu ? (bồn không chứa nước)

 

Hướng dẫn giải

Bài 86 (Sách bài tập - tập 2 - trang 157)

Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng theo hình 165.

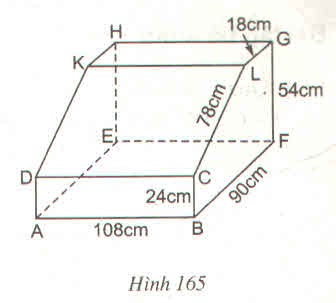
Các kích thước của nó là :

AB = 108 cm, BC = 24 cm, BF = 90 cm, FG = 54 cm, LG = 18 cm, LC = 78 cm

Các cạnh AB, DC, EF, HG và KL đều vuông góc với mặt phẳng (ADKHE)  và LG song song với BF

a) Diện tích hình chữ nhật CDKL

b) Diện tích hình thang BCLGF

c) Thể tích hình lăng trụ đứng ADKHE.BCLGF

Hướng dẫn giải

a) \(S_{CDKL}=0,8424m^2\)

b) \(S_{BCLGF}=0,378m^2\)

c) 408 240cm³ = 0,41m³

Bài 76 (Sách bài tập - tập 2 - trang 154)

Tính diện tích toàn phần của lăng trụ đứng theo các kích thước cho ở hình 158 ?

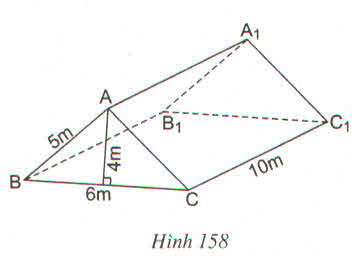
Hướng dẫn giải

Diện tích đáy ABC: S₁= 1/2.6.4=12 (m²)

Diện tích mặt BCC₁B₁: S₂=6.10=60 (m²⁾

Diện tích AA₁C₁C: S₃₌ 10.5=50 (m²)

Ta thấy hai mặt AA₁B₁B và AA₁C₁C bằng nhau nên:

S_tp= 2S₁+S₂+2S₃= 2.12+60+2.50= 184 (m²)

Bài 84 (Sách bài tập - tập 2 - trang 156)

Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình 164.

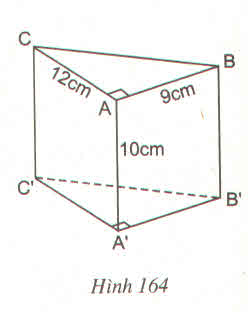
Hướng dẫn giải

áp dụng định lí Py-ta-go vào \(\Delta\)ABC vuông tại A:

BC=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{9^2+12^2}\)=15(cm)

S_xq=(12+9+15).10=360(cm²)

Sđ=12.9:2=54(cm²)

S_tp=S_xq+2Sđ=360+2.54=468(cm²)

V=Sđ.h=54.10=540(cm³)

Bài 73 (Sách bài tập - tập 2 - trang 153)

Xét hình lập phương (h.155).

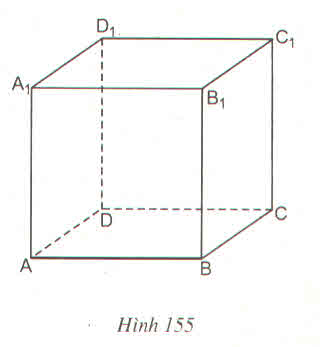
Hãy chỉ ra :

a) Hai đường thẳng cắt nhau

b) Hai đường thẳng song song

c) Hai đường thẳng không cắt nhau và không nằm trong một mặt phẳng

d) Đường thẳng nằm trong mặt phẳng

e) Đường thẳng không có điểm chung với mặt phẳng

f) Đường thẳng cắt mặt phẳng

g) Hai mặt phẳng cắt nhau

h) Hai mặt phẳng không cắt nhau

i) Hai mặt phẳng vuông góc với nhau 

Hướng dẫn giải

Bài 88 (Sách bài tập - tập 2 - trang 157)

Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' có các cạnh đáy là a và 2 a, chiều cao của mặt bên là a

a) Tính diện tích xung quanh của hình chóp cụt

b) Tính độ dài cạnh bên và chiều cao hình chóp cụt

Hướng dẫn giải

\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)

\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)

Trong tamn giác vuông A^'HA:

\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)

Từ đó tính tiếp sẽ ra chiều cao hình chóp

Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)

Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)

Bài 83 (Sách bài tập - tập 2 - trang 156)

Một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao lăng trụ là 7cm. Độ dài hai cạnh góc  vuông của đáy là 3cm và 4 cm. Hãy tính :

a) Diện tích một mặt đáy

b) Diện tích mặt xung quanh

c) Diện tích toàn phần

d) Thể tích lăng trụ

Hướng dẫn giải

a, Diện tích một mặt đáy: 1/2.3.4= 6 (cm²)

b, Diện tích xung quanh: 7.(3+4+5)=84 (cm²)

c, Diện tích toàn phần: 84+2.6= 96 (cm²)

d, Thể tích lăng trụ: V= 7.6=42 (cm³)

Bài 90 (Sách bài tập - tập 2 - trang 157)

Tính thể tích của một trụ bê tông cho theo các kích thước ở hình 166, SJ = 9, OI = IJ

Phần trên là một hình hộp chữ nhật, phần dưới là một hình chóp cụt tứ giác đều.

Hướng dẫn giải

Thể tích hình hộp chữ nhật là V₁ = 5.5.3 = 75

Vì OI = IJ , IJ = AA' = 3 và SJ = 9 nên OI = 3 và SO = 3

\(\Rightarrow A_1B_1C_1D_1\) là hình vuông cạnh 2,5

Vậy thể tích hình chóp S.A₁B₁C₁D₁ là :

\(V_2=\dfrac{1}{3}.3.2,5.2,5=6,25\)

Thể tích hình chóp S.A'B'C'D' là :

\(V_3=\dfrac{1}{3}.6.5.5=50\)

Vậy thể tích cần tính là : \(V=V_1+V_3-V_2=118,75\)

Bài IV.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 158)

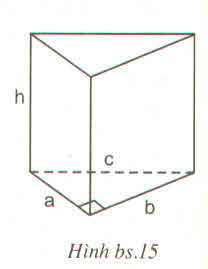
Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau :

Hướng dẫn giải

a	9	35	20	63	28
b	40	12	21	16	45
c	41	37	29	65	53
h	8	18	17	24	13
Diện tích 1 đáy	180	210	210	504	630
Diện tích xung quanh	720	1512	1190	3456	1638
Diện tích toàn phần	1080	1932	1610	4464	2898
Thể tích	1440	3780	3570	12096	8190

Bài 87 (Sách bài tập - tập 2 - trang 157)

Thể tích của một hình chóp đều là \(126cm^3\), chiều cao của hình chóp là 6cm. Như vậy :

Trong các số dưới đây, số nào là diện tích đáy của nó ?

(A) \(45cm^2\)                        (B) \(52cm^2\)                              (C) \(63cm^2\)

(D) \(60cm^2\)                        (E) \(50cm^2\)                              

Hướng dẫn giải

Ta có:

\(V=\dfrac{1}{3}.S.h\Rightarrow S=\dfrac{V.3}{h}\)

\(\Rightarrow S=\dfrac{126.3}{6}=63cm^2\)

Vậy chọn phương án (C)63cm²

Bài IV.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 159)

Hướng dẫn giải

a	6	16	24	32	16
d	5	10	15	20	17
h	4	6	9	12	15
Diện tích đáy	36	256	576	1024	256
Diện tích xung quanh	60	320	720	1280	544
Diện tích toàn phần	96	576	1296	2304	800
Thể tích	48	512	1728	4096	1280

Bài 74 (Sách bài tập - tập 2 - trang 154)

Trên hình 156 : l, v, h là ba kích thước của một hình hộp chữ nhật. Hãy điền số thích hợp vào các ô trống ở bảng sau :

 

Hướng dẫn giải

l	25	8	15	8
v	20	4	12	6
h	10	6	4	12
Sxq	900	144	216	336
Stp	1900	208	576	432
V	5000	192	720	576

Bài IV.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 158)

Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu tăng :

a) Gấp đôi chiều cao của hình chóp

b) Gấp đôi cạnh đáy của hình chóp

c) Gấp đôi cả chiều cao và cạnh đáy của hình chóp

Hướng dẫn giải

Tam giác đều cạnh a có diện tích bằng \(\dfrac{a^2\sqrt{3}}{4}\) . Do đó , hình chóp tam giác đều với cạnh đáy a , chiều cao h có thể tích :

\(V=\dfrac{1}{3}.\dfrac{a^2\sqrt{3}}{4}.h=\dfrac{a^2h\sqrt{3}}{12}\)

a) Nếu tăng gấp đôi chiều cao thì thể tích hình chóp là

\(V'=\dfrac{1}{3}.\dfrac{a^2\sqrt{3}}{4}.2h=2.\dfrac{a^2h\sqrt{3}}{12}=2V\)

b) Nếu tăng gấp đôi cạnh đáy thì thể tích hình chóp là

\(V'=\dfrac{1}{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}.h=4.\dfrac{a^2h\sqrt{3}}{12}=4V\)

c) Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là

\(V'=\dfrac{1}{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}.2h=8.\dfrac{a^2h\sqrt{3}}{12}=8V\)