Tính chất ba đường cao của tam giác
Bài 9.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 52)
Cho tam giác ABC không là tam giác cân. Khi đó trực tâm của tam giác ABC là giao điểm của :
(A) Ba đường trung tuyến (B) Ba đường phân giác
(C) Ba đường trung trực (D) Ba đường cao
Hãy chọn phương án đúng ?
Hướng dẫn giải
Bài 72 (Sách bài tập - tập 2 - trang 51)
Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC ?
Hướng dẫn giải
Giải
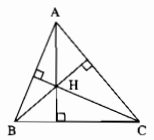
Trong ∆ABC ta có H là trực tâm nên
\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)
Trong ∆AHB ta có:
\(\text{AC⊥BH }\)
\(\text{BC⊥AH}\)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\text{BA⊥CH}\)
\(\text{CB⊥BH}\)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\text{BA⊥HC}\)
\(\text{CA⊥BH}\)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.
Bài 77 (Sách bài tập - tập 2 - trang 51)
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của tam giác ABC, đường cao AF của tam giác ACD.
Chứng minh rằng :
\(\widehat{EAF}=90^0\)
Hướng dẫn giải
a) \(\Delta ABC\) cân tại A, AE là đường cao nên đồng thời AE là đường phân giác.
\(\Delta ACD\) cân tại A, AF là đường cao nên đồng thời là AF là đường phân giác.
AE và AF là các tia phân giác của hai góc kề bù \(\widehat{BAC},\widehat{CAD}\) nên AE \(\perp\) AF hay \(\widehat{EAF}=90^o\).
Bài 79 (Sách bài tập - tập 2 - trang 51)
Tam giác ABC có AB = AC = 13cm, BC = 10 cm. Tính độ dài đường trung tuyến AM ?
Hướng dẫn giải
Bài 70 (Sách bài tập - tập 2 - trang 50)
Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó ?
Hướng dẫn giải
Bài 73 (Sách bài tập - tập 2 - trang 51)
Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó cân ?
Hướng dẫn giải
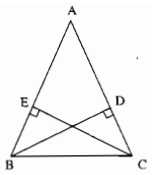
Xét hai tam giác vuông BDC và CEB:
góc BDC= góc CEB=90∘
BD = CE (gt)
BC cạnh huyền chung
Do đó: ∆BDC = ∆CEB (cạnh huyền, cạnh góc vuông)
⇒ góc DCB= góc EBC
Hay góc ACB= góc ABC
Vậy ∆ABC cân tại A.
Bài 9.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 51)
Hãy chọn khẳng định đúng trong các khẳng định sau :
(A) Trực tâm của một tam giác bao giờ cũng nằm trong tam giác
(B) Trực tâm của một tam giác bao giờ cũng nằm ngoài tam giác
(C) Trực tâm của một tam giác bao giờ cũng trùng với một đỉnh của tam giác
(D) Cả ba khẳng định trên đều sai
Hướng dẫn giải
Bài 78 (Sách bài tập - tập 2 - trang 51)
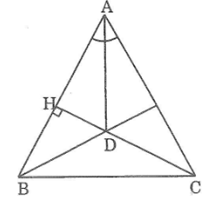
Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC ?
Hướng dẫn giải
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
Bài 74 (Sách bài tập - tập 2 - trang 51)
Tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của các tam giác ABC, AHB, AHC ?
Hướng dẫn giải
Bài 76 (Sách bài tập - tập 2 - trang 51)
Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua A kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC ?
Hướng dẫn giải
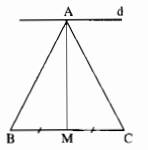
∆ABC cân tại A, AM là đường trung tuyến nên AM cũng là đường cao.
AM⊥BC
d⊥AM(gt)
Suy ra: d // BC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba).
Bài 9.5 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 52)
Chứng minh rằng trong một tam giác, tia phân giác của một góc trong và hai tia phân giác của hai góc ngoài không kề với nó đồng quy tại một điểm, điểm đó cách đều ba đường thẳng chứa ba cạnh của tam giác ?
Hướng dẫn giải
Bài 9.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 52)
Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Hãy tính góc \(AMB\) biết \(\widehat{A}=55^0,\widehat{B}=67^0\)
Hướng dẫn giải
Bài 9.6 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 52)
Cho tam giác ABC. Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A', B', C'. Chứng minh rằng AA', BB', CC' là các đường cao của tam giác A'B'C'. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C' ?
Hướng dẫn giải
Bài 9.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 52)
Cho tam giác ABC cân tại đỉnh A. Hai đường cao xuất phát từ đỉnh B và đỉnh C cắt nhau tại M. Hãy tìm các góc của tam giác ABC, biết \(\widehat{BMC}=140^0\) ?
Hướng dẫn giải
Bài 81* (Sách bài tập - tập 2 - trang 51)

Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (h.17)
a) Chứng minh rằng A là trung điểm của EF
b) Các đường cao của tam giác ABC là các đường trung trục của tam giác nào ?
Hướng dẫn giải

a,
Theo bài ra ta có:
+)FE//BC
+)EC//BA hay ED//BA
+)AC//FB hay AC//FD
Khi đó:
+)\(\widehat{FBA}=\widehat{BAC}\)
+)\(\widehat{B\text{AF}}=\widehat{ABC}\)
Vì BF//AC
Xét \(\Delta FBA\) và \(\Delta CAB\) có:
\(\left\{{}\begin{matrix}\widehat{B\text{AF}}=\widehat{ABC}\\BAchung\\\widehat{FBA}=\widehat{BAC}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA\) = \(\Delta CAB\) (g.c.g)
=> FB=AC ( hai cạnh tương ứng )
Ta lại có:
+) \(\widehat{FAB}=\widehat{CEA}\)
+) \(\widehat{BFA}=\widehat{CAE}\)
( vì BF//CA và BA//CE )
=> \(\widehat{FBA}=\widehat{ACE}\)
Xét \(\Delta FBA\) và \(\Delta ACE\) có:
\(\left\{{}\begin{matrix}\widehat{BFA}=\widehat{CAE}\\FB=AC\\\widehat{FBA}=\widehat{ACE}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA=\Delta ACE\left(g.c.g\right)\)
=> FA=EA ( hai cạnh tương ứng )
Mà F;A;E thẳng hàng
=> A là trung điểm của EF
(đ.p.c.m)
b,
Các đường cao của tam giác ABC là các đường trung trực của tam giác DFE
Bài 80 (Sách bài tập - tập 2 - trang 51)
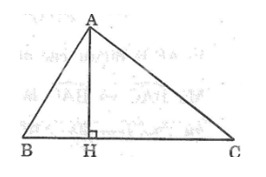
Cho tam giác ABC có góc B và góc C là các góc nhọn, AC > AB. Kẻ đường cao AH.
Chứng minh rằng :
\(\widehat{HAB}< \widehat{HAC}\)
Hướng dẫn giải
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Bài 75 (Sách bài tập - tập 2 - trang 51)
Cho hình 16.
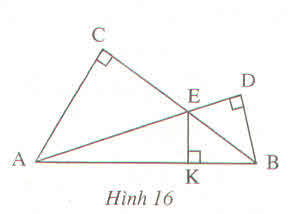
Có thể khẳng định rằng các đường thẳng AC, BD, KE cùng đi qua một điểm hay không ? Vì sao ?
Hướng dẫn giải
Bài 71 (Sách bài tập - tập 2 - trang 50)
Cho hình 15 :

a) Chứng minh : \(CI\perp AB\) ?
b) Cho \(\widehat{ACB}=40^0\) . Tính \(\widehat{BID},\widehat{DIE}\) ?