Tính chất đường trung trực của một đoạn thẳng
Bài 7.6 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 49)
Cho đường thẳng d và hai điểm A, B nằm về một phía của d sao cho AB không vuông góc với d. Hãy tìm trên d một điểm M sao cho \(\left|MA-MB\right|\) có giá trị nhỏ nhất ?
Hướng dẫn giải
Ta có: \(\left|MA-MB\right|\ge0\) với một điểm M tùy ý.
\(\left|MA-MB\right|=0\) chỉ với điểm M mà MA = MB
=> M nằm trên đường trung trực của đoạn thẳng AB. (Có giao điểm này vì AB không vuông góc với đường thẳng d)
Vậy, \(\left|MA-MB\right|\) đạt GTNN là 0 khi M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB.
Bài 7.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 48)
Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng ?
a) \(\widehat{AMN}\ne\widehat{BMN}\) b) \(\widehat{MAN}\ne\widehat{MBN}\)
c) \(\widehat{MNA}\ne\widehat{MNB}\) d) \(\Delta AMN=\Delta BMN\)
Hướng dẫn giải
Bài 7.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 49)
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng :
a) D là trung điểm của cạnh BC
b) \(\widehat{A}=\widehat{B}+\widehat{C}\)
Hướng dẫn giải
Bài 56 (Sách bài tập - tập 2 - trang 47)
Cho đường thẳng d và hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ d. Tìm một điểm C nằm trên d sao cho C cách đều A và B ?
Hướng dẫn giải
Bài 63 (Sách bài tập - tập 2 - trang 48)
Hai nhà máy được xây dựng tại hai địa điểm A và B nằm về một phía của khúc sông thẳng. Tìm trên bờ sông một địa điểm C để xây một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B là nhỏ nhất ?
Hướng dẫn giải
Bài 7.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 49)
Cho hai tam giác cân chung đáy ABC và ABD, trong đó ABC là tam giác đều. Gọi E là trung điểm của AB. Khi đó, khẳng định nào sau đây sai ?
(A) Đường thẳng CD là đường trung trực của AB
(B) Điểm E không nằm trên đường thẳng CD
(C) Đường trung trực của AC đi qua B
(D) Đường trung trực của BC đi qua A
Hướng dẫn giải
Bài 7.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 49)
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm :
a) AD và CD nếu BD = 5cm, AC = 8cm
b) AC nếu BD = 11,4cm; AD = 3,2 cm
Hướng dẫn giải
Bài 57 (Sách bài tập - tập 2 - trang 47)
Đường trung trục d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như trên hình 10. Cho điểm M thuộc phần I và điểm N thuộc phần II.
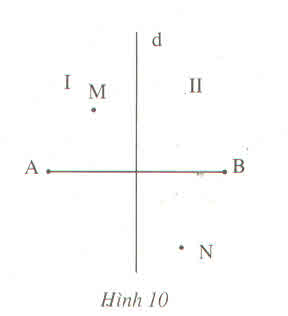
Chứng minh rằng :
a) MA < MB
b) NA > NB
Hướng dẫn giải
Bài 62 (Sách bài tập - tập 2 - trang 48)
Cho hình 12, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC
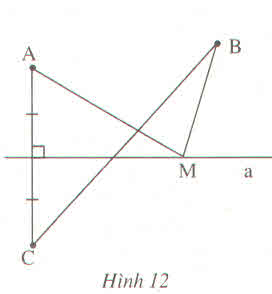
a) Hãy so sánh MA + MB với BC
b) Tìm vị trí của điểm M trên đường thẳng a để MA + MB là nhỏ nhất ?
Hướng dẫn giải
Bài 7.5 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 49)
Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC ?
Hướng dẫn giải
Bài 58 (Sách bài tập - tập 2 - trang 48)
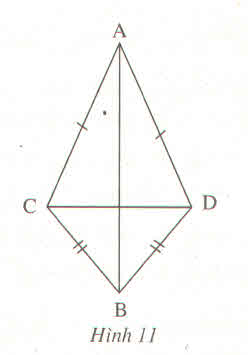
Cho hình 11. Chứng minh rằng AB vuông góc với CD
Hướng dẫn giải
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD
Bài 59 (Sách bài tập - tập 2 - trang 48)
Cho hai điểm A, B và một đường thẳng d. Vẽ đường tròn tâm O đi qua hai điểm A, B sao cho O nằm trên đường thẳng d ?
Hướng dẫn giải
Bài 60 (Sách bài tập - tập 2 - trang 48)
Cho đoạn thẳng AB. Tìm tập hợp các điểm C sao cho tam giác ABC là tam giác cân có đáy là AB ?
Hướng dẫn giải
Bài 54 (Sách bài tập - tập 2 - trang 47)
Cho ba tam giác cân ABC, DBC, EBC chung đáy BC.
Chứng minh rằng ba điểm A, D, E thẳng hàng ?
Hướng dẫn giải
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
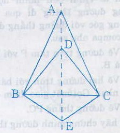
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Bài 55 (Sách bài tập - tập 2 - trang 47)
Cho hai điểm D, E nằm trên đường trung trực của đoạn thẳng BC.
Chứng minh rằng :
\(\Delta BDE=\Delta CDE\)
Hướng dẫn giải
Bài 61 (Sách bài tập - tập 2 - trang 48)
Cho góc xOy bằng \(60^0\), điểm A nằm trong góc xOy. Vẽ điểm B sao cho Ox là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trung trực của AC
a) Chứng minh OB = OC
b) Tính số đo góc BOC
Hướng dẫn giải
Giải :
a, Ox là đường trung trực của AB nên OA=OB
Oy là đường trung trực của AC nên OA=OC
=> OB=OC
b, Xét tg AOB cân tại O ( do OA=OB )
=> góc O1= góc O2 = 1/2 góc AOB
Xét tg AOC cân tại o ( vì OA=OC )
=> góc O3 = góc O4 = 1/2 góc AOC
nên góc AOB+ góc AOC= 2 (góc O1+góc O3)
= 2.góc xOy
= 2.60 độ
= 120 độ
Vậy góc BOC = 120 độ
( Hình thì dễ nên bạn tự vẽ nhé )




