Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Lý thuyết

Bài 14 (Sách bài tập - tập 2 - trang 38)

Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ tử A và C đến đường thẳng BD. So sánh AC với tổng AE + CF ?

Hướng dẫn giải

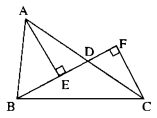
Trong ∆ADE ta có

Nên AE < AD (1)

Trong ∆CFD ta có

Nên CF < CD (2)

Cộng từng vế (1) và (2) ta có:

AE + CF < AD + CD

Mà D nằm giữa A và C nên AD + CD = AC

Vậy AE + CF < AC

Bài 2.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

Cho tam giác ABC vuông tại A. Gọi BD là đường phân giác của góc B ( \(D\in AC\)). Chứng minh rằng BD < BC ?

Hướng dẫn giải

Vì BD là tia phân giác \(\widehat{ABC}\)

=> BD nằm giữa BA và BC

=> điểm D nằm giữa A và C hay AD < AC

AC là hình chiếu của đường xiên BC

AD là hình chiếu của đường xiên BD

mà AD < AC

=> BC < BD

Bài 12 (Sách bài tập - tập 2 - trang 38)

Cho hình 2.

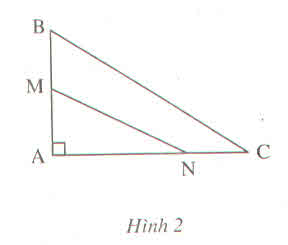
Chứng minh rằng MN < BC ?

Hướng dẫn giải

Hình chiếu của AN < hình chiếu của AC

=> đường xiên BN < đường xiên của BC (1)

Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)

Từ (1) và (2) suy ra:

MN< BN< BC.

Bài 2.6 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

Cho điểm P nằm ngoài đường thẳng d 

a) Hãy nêu cách vẽ hai đường xiên PQ, PR sao cho PQ = PR và \(\widehat{QPR}=60^0\)

b) Trong hình dựng được ở câu a), cho PQ = 18 cm. Tính độ dài hình chiếu của hai đường xiên PQ, PR trên d

Hướng dẫn giải

Bài 2.5 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

Cho điểm A nằm ngoài đường thẳng xy

a) Tìm trên đường thẳng xy hai điểm M, N sao cho hai đường xiên AM và AN bằng nhau ?

b) Lấy một điểm D trên đường thẳng xy. Chứng minh rằng :

- Nếu D ở giữa M và N thì AD < AM

- Nếu D không thuộc đoạn thẳng MN thì AD > AM

Hướng dẫn giải

Bài 17 (Sách bài tập - tập 2 - trang 38)

Cho hình 3 trong đó AB > AC. 

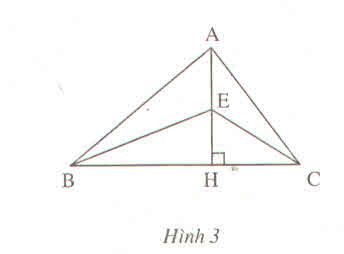
Chứng minh rằng EB > EC ?

Hướng dẫn giải

Ta có: AB > AC (gt)

Suy ra: HB > HC (đường xiên lớn hơn có hình chiếu lớn hơn)

Suy ra: EB > EC (hình chiếu lớn hơn thì có đường xiên lớn hơn)

Bài 18 (Sách bài tập - tập 2 - trang 38)

Cho hình 4, chứng minh rằng :

                      \(BD+CE< AB+AC\)

 

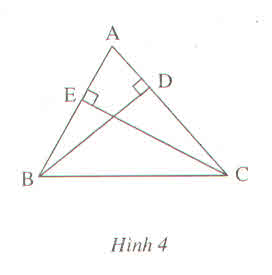
Hướng dẫn giải

Bài 16 (Sách bài tập - tập 2 - trang 38)

Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC ?

Hướng dẫn giải

Kẻ \(AH\perp BC\)

- Nếu D trùng H thì \(AD< AC\) vì \(AH< AC\) ( đường vuông góc nhỏ hơn đường xiên )

- Nếu D không trùng H, giả sử D nằm giữa H và C. Ta có: \(HD< HC\)

\(\Rightarrow AD< AC\) ( hình chiếu nhỏ hơn thì đường xiên nhỏ hơn )

Vậy AD nhỏ hơn cạnh bên của \(\Delta ABC\)

Bài 11 (Sách bài tập - tập 2 - trang 38)

Cho hình 1.

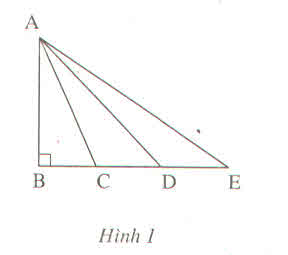
So sánh các độ dài AB, AC, AD, AE ?

Hướng dẫn giải

Điểm C nằm giữa B và D nên BC < BD (1)

Điểm C nằm giữa B và E nên BD < BE (2)

Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra

BC < BD < BE

Suy ra: AB < AC < AD < AE.

Bài 2.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

Cho đường thẳng d và điểm A không thuộc d. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai ?

(A) Có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d

(B) Có duy nhất một đường xiên kẻ từ điểm A đến đường thẳng d

(C) Có vô số đường vuông góc kẻ từ điểm A đến đường thẳng d

(D) Có vô số đường xiên kẻ từ điểm A đến đường d

Hãy vẽ hình minh hoạ cho các khẳng định đúng ?

Hướng dẫn giải

a, Đ

b, S

c, S

d, Đ

Bài 13 (Sách bài tập - tập 2 - trang 38)

Cho tam giác ABC cân tại A có AB = AC = 10 cm, BC = 12 cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không, có cắt cạnh BC hay không ? Vì sao ?

Hướng dẫn giải

Bài 2.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

Qua điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH và các đường xiên AB, AC đến đường thẳng d (H, B, C đều thuộc d). Biết rằng HB < HC. Hãy chọn khẳng định đúng trong các khẳng định sau :

(A) AB > AC                        (B) AB = AC

(C) AB < AC                         (D) AH > AB

Hướng dẫn giải

Theo định lí so sánh giữa hình chiếu và đường xiên ta có:

\(HB< HC\Rightarrow AB< AC.\)

Vậy nên chọn đáp án C

Bài 15 (Sách bài tập - tập 2 - trang 38)

Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM.

Chứng minh rằng :       \(AC< \dfrac{BE+BF}{2}\)

 

Hướng dẫn giải

\(\Delta ABM\) vuông tại \(A\Rightarrow AB< BM\)

Do đó: \(AB< BE+ME\) __(1)__

Và \(AB< BF-MF\) __(2)__

\(\Delta MAE=\Delta MCF\) ( cạnh huyền - góc nhọn )

\(\Rightarrow ME=MF\) __(3)__

Từ (1),(2),(3) suy ra:

\(AB+AB< BE+BF\)

Do đó

\(2AB< BE+BF\) nên \(AB< \dfrac{BE+BF}{2}\)

Bài 2.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 39)

a) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lí Pitago, chứng minh rằng BC > B'C'

b) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'.  Không sử dụng định lí Pitago, chứng minh rằng AC > A'C'

Hướng dẫn giải