Lũy thừa của một số hữu tỉ (tiếp theo...)
Bài 34 (SGK tập 1 - Trang 22)
Trong vở bài tập của bạn Dũng có bài làm sau :
a) \(\left(-5\right)^2.\left(-5\right)^3=\left(-5\right)^6\)
b) \(\left(0,75\right)^3:0,75=\left(0,75\right)^2\)
c) \(\left(0,2\right)^{10}:\left(0,2\right)^5=\left(0,2\right)^2\)
d) \(\left[\left(-\dfrac{1}{7}\right)^2\right]^4=\left(-\dfrac{1}{7}\right)^6\)
e) \(\dfrac{50^3}{125}=\dfrac{50^3}{5^3}=\left(\dfrac{50}{5}\right)^3=10^3=1000\)
Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có)
f) \(\dfrac{8^{10}}{4^8}=\left(\dfrac{8}{4}\right)^{10-8}=2^2\)
Hướng dẫn giải
Các câu sai: a, c, d, f
Các câu đúng: b, e
Bài 35 (SGK tập 1 - Trang 22)
Ta thừa nhận tính chất sau đây :
Với \(a\ne0;a\ne\pm1\), nếu \(a^m=a^n\) thì \(m=n\)
Dựa vào tính chất này, hãy tìm các số tự nhiên m và n biết :
a) \(\left(\dfrac{1}{2}\right)^m=\dfrac{1}{32}\)
b) \(\dfrac{343}{125}=\left(\dfrac{7}{5}\right)^n\)
Hướng dẫn giải
a) =>
b) =>
Bài 36 (SGK tập 1 - Trang 22)
Viết các biểu thức sau đây dưới dạng lũy thừa của một số hữu tỉ :
a) \(10^8.2^8\)
b) \(10^8:2^8\)
c) \(25^4.2^8\)
d) \(15^8.9^4\)
e) \(27^2:25^3\)
Hướng dẫn giải
a)
b) =
c) =
d) =
e) =
Bài 37 (SGK tập 1 - Trang 22)
Tìm giá trị của các biểu thức sau :
a) \(\dfrac{4^2.4^3}{2^{10}}\)
b) \(\dfrac{\left(0,6\right)^5}{\left(0,2\right)^6}\)
c) \(\dfrac{2^7.9^3}{6^5.8^2}\)
d) \(\dfrac{6^3+3.6^2+3^3}{-13}\)
Hướng dẫn giải
a) =
b) =
c) =
d) =
Luyện tập - Bài 38 (SGK tập 1 - Trang 22)
a) Viết các số \(2^{27}\) và \(3^{18}\) dưới dạng các lũy thừa có số mũ là 9
b) Trong hai số \(2^{27}\) và \(3^{18}\), số nào lớn hơn ?
Hướng dẫn giải
a) Ta có:
b) Vì 8< 9 nên \(8^9< 9^9\)
Vậy theo câu a, ta được \(3^{18}< \) \(2^{27}\)
Luyện tập - Bài 39 (SGK tập 1 - Trang 23)
Cho \(x\in\mathbb{Q};x\ne0\). Viết \(x^{10}\) dưới dạng :
a) Tích của hai lũy thừa trong đó có một thừa số là \(x^7\)
b) Lũy thừa của \(x^2\)
c) Thương của hai lũy thừa trong đó số bị chia là\(x^{12}\)
Hướng dẫn giải
a) \(x^{10}=x^7.x^3\)
b) \(x^{10}=\left(x^2\right)^5\)
c) \(x^{10}=x^{12}:x^2\)
Luyện tập - Bài 40 (SGK tập 1 - Trang 23)
Tính :
a) \(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2\)
b) \(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2\)
c) \(\dfrac{5^4.20^4}{25^5.4^5}\)
d) \(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{-6}{5}\right)^4\)
Hướng dẫn giải
a) 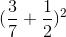 =
= 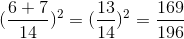
b) 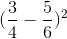 =
= 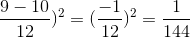
c) 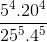 =
= 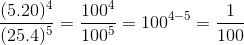
d) 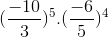 =
= 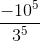 .
. 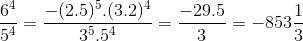
Luyện tập - Bài 41 (SGK tập 1 - Trang 23)
Tính :
a) \(\left(1+\dfrac{2}{3}-\dfrac{1}{4}\right).\left(\dfrac{4}{5}-\dfrac{3}{4}\right)^2\)
b) \(2:\left(\dfrac{1}{2}-\dfrac{2}{3}\right)^3\)
Hướng dẫn giải
a) 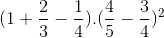 =
= 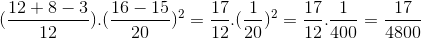
b) 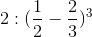 =
= 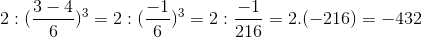
Luyện tập - Bài 42 (SGK tập 1 - Trang 23)
Tìm số tự nhiên n, biết :
a) \(\dfrac{16}{2^n}=2\)
b) \(\dfrac{\left(-3\right)^n}{81}=-27\)
c) \(8^n:2^n=4\)
Hướng dẫn giải
a) 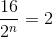
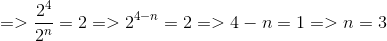
b) 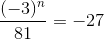
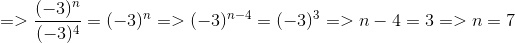
c) 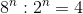
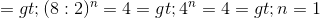
Luyện tập - Bài 43 (SGK tập 1 - Trang 23)
Đố :
Biết rằng \(1^2+2^2+3^2+.....+10^2=385\)
Đố em tính nhanh được tổng :
\(S=2^2+4^2+6^2+.....+20^{^{ }2}\)
Hướng dẫn giải
S = 22 + 42 + 62 + ... + 202
= (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2
= 22.12 + 22 .22 + 22 .32 + ... + 22 .102
= 22 (12 + 22 + ... +102 )
= 4 . 385 = 1540




