Đường thẳng đi qua hai điểm
Bài 15 (Sách giáo khoa trang 109)
Quan sát hình 21 và cho biết những nhận xét sau đúng hay sai :
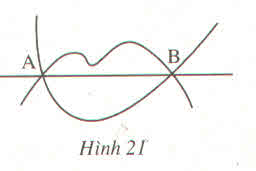
a) Có nhiều đường "không thẳng" đi qua hai điểm A và B
b) Chỉ có một đường thẳng đi qua hai điểm A và B
Hướng dẫn giải
a) Đúng. Hai đường "không thẳng" chính là hai đường cong như trên hình.
b) Đúng. Đó chính là đường thẳng AB.
Bài 16 (Sách giáo khoa trang 109)
a) Tại sao không nói : "Hai điểm thẳng hàng" ?
b) Cho ba điểm A, B, C trên trang giấy và một thước thẳng (không chia khoảng). Phải kiểm tra như thế nào để biết được ba diểm đó có thẳng hàng hay không ?
Hướng dẫn giải
a, Qua hai điểm bao giờ cũng có một đường thẳng nên ta không nói hai điểm thẳng hàng.
b, Đặt cạnh thước đi qua hai điểm, chẳng hạn A,B. Nếu C nằm trên cạnh thước thì ba điểm đó thẳng hàng, trái lại thì ba điểm đó không thẳng hàng.
Bài 17 (Sách giáo khoa trang 109)
Lấy 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm. Có tất cả bao nhiêu đường thẳng ? Đó là những đường thẳng nào ?
Hướng dẫn giải
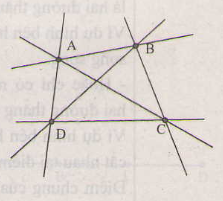
Qua điểm A và mỗi điểm B, C, D có ba đường thằng là AB, AC, AD. Qua điểm B và mỗi điểm C, D có hai đường thẳng là BC, BD (Không qua A). Qua điểm C và D còn lại có một đường thẳng CD (không đi qua A, B).
Chú ý: có thể trình bày ngắn gọn như sau : với 4 điểm A, B, C, D thì có 6 đường thẳng AB, AC, AD, BC, BD, CD.
Lưu ý: Ta có thể chứng minh được: với n điểm, trong đó không có 3 điểm nào thẳng hàng thì số đường thẳng kẻ được là: công thức; đường thẳng.
Dựa vào công thức trên, ta có bải toán đảo: cho trước một số điểm trong đó không có ba điểm nào thẳng hàng. vẽ các đường thẳng đi qua các cặp điẻm. Biết số đường thẳng vẽ được là 6. Hỏi tất cả có bao nhiêu điểm cho trước.
Bài 18 (Sách giáo khoa trang 109)
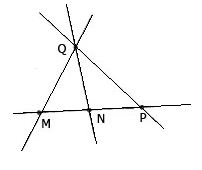
Lấy bốn điểm M, N, P, Q trong đó 3 điểm M, N, P thẳng hàng và điểm Q nằm ngoài đường thẳng kẻ trên. Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng (phân biệt) ? Viết tên các đường thẳng đó ?
Hướng dẫn giải
- Vì ba điểm M, N, P thẳng hàng nên qua ba điểm này sẽ có 1 đường thẳng.
- Qua Q và mỗi điểm M, N, P ta sẽ vẽ được 3 đường thẳng là QM, QN, QP.
Vậy ta sẽ vẽ được tất cả 4 đường thẳng là MP, QM, QN, QP.
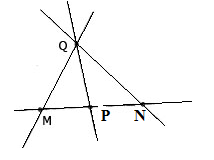
Ngoài ra, vì đề bài không nhắc đến vị trí của M, N, P nên các bạn cũng có thể vẽ như sau:
Bài 19 (Sách giáo khoa trang 109)
Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng \(d_1\) và điểm T trên đường thẳng \(d_2\) sao cho X, Z, T thẳng hàng và Y, Z, T thẳng hàng ?
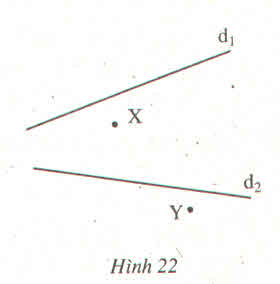
Hướng dẫn giải
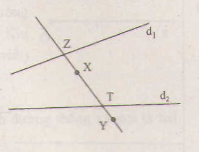
- Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Bài 20 (Sách giáo khoa trang 109)
Vẽ hình theo các cách diễn đạt sau :
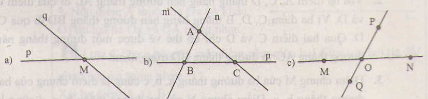
a) M là giao điểm của hai đường thẳng p và q
b) Hai đường thẳng m và n cắt nhau tại A, đường thẳng p cắt n tại B và cắt m tại C
c) Đường thẳng MN và đường thẳng PQ cắt nhau tại O
Hướng dẫn giải
Bài 21 (Sách giáo khoa trang 110)
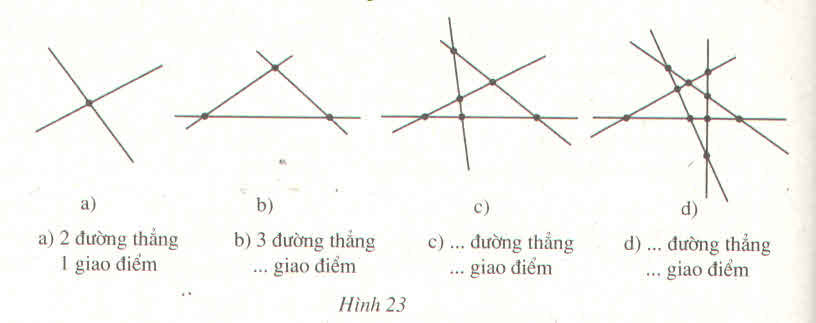
Xem hình 23 rồi điển vào chỗ trống :
Hướng dẫn giải
Cách làm bài này là các bạn đếm số đường thẳng cũng như số giao điểm để điền vào chỗ trống:
a) 2 đường thẳng 1 giao điểm
b) 3 đường thẳng 3 giao điểm
c) 4 đường thẳng 6 giao điểm
d) 5 đường thẳng 10 giao điểm