Tính chất của phép cộng các số nguyên
Bài 62 (Sách bài tập - tập 1 - trang 75)
Tính các tổng :
a) \(-11+y+7\)
b) \(x+22+\left(-14\right)\)
c) \(a+\left(-15\right)+62\)
Hướng dẫn giải
a) -11 + y + 7
= (-11 + 7) + y
= y - 4
b) x + 22 + (-14)
= x + (22 - 14)
= x + 8
c) a + (-15) + 62
= a + (62 - 15)
= a + 47
Bài 6.4 (Sách bài tập - tập 1 - trang 77)
Tìm \(x\in\mathbb{Z}\), biết :
\(x+\left(-23\right)=\left(-100\right)+77\)
Hướng dẫn giải
\(x+\left(-23\right)=\left(-100\right)+77\\ x-23=-23\\ x=-23+23\\ x=0\)
Vậy \(x=0\).
Bài 70* - Luyện tập (Sách bài tập - tập 1 - trang 77)
| \(x\) | -5 | 7 | -2 |
| \(y\) | 3 | -14 | -2 |
| \(\left|x+y\right|\) | |||
| \(\left|x+y\right|+x\) |
Hướng dẫn giải
| -5 | 7 | -2 | |
| 3 | -14 | -2 | |
| 2 | 7 | 4 | |
| -3 | 14 | 2 |
Bài 6.5 (Sách bài tập - tập 1 - trang 77)
Cho \(a\in\mathbb{Z}\). Tính tổng :
\(S=a+\left|a\right|+a+\left|a\right|+....+a+\left|a\right|\) gồm 50 số hạng
Hướng dẫn giải
Vì a\(\in\)Z nên a có thể lớn hơn 0, nhỏ hơn 0 hoặc bằng 0.
Nếu a>0 thì \(\left|a\right|=a\), nên S=50a.
Nếu a<0 thì \(a+\left|a\right|=0\),nên S=0.
Nếu a=0 thì S=0.
Bài 65 - Luyện tập (Sách bài tập - tập 1 - trang 76)
Tính :
a) \(\left(-57\right)+47\)
b) \(469+\left(-219\right)\)
c) \(195+\left(-200\right)+205\)
Hướng dẫn giải
a) ( -57) + 47 = -10
b) 469 + (-219) = 250
c) 195 + (-200) + 205 = 200
Bài 6.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 76)
Với mỗi phát biểu sai ở câu 6.1, hãy tìm một ví dụ để chứng tỏ điều đó ?
Hướng dẫn giải
a) Đúng
b) Sai.
VD: 2 và -2 là số nguyên, -2 + 2 = 0
c) Đúng
d) Sai.
VD: |2| + |-5| \(\ne\) |2+ (-5)| ( 7 \(\ne\) -3 )
Bài 69 - Luyện tập (Sách bài tập - tập 1 - trang 76)
Đố vui :
Hai bạn Hồng và Hà tranh luận với nhau : Hồng bảo rằng có hai số nguyên mà tổng của chúng nhỏ hơn một số hạng và lớn hơn số hạng kia. Hà bảo rằng không thể có được. Theo bạn : Ai đúng ? Nêu một ví dụ làm căn cứ ?
Hướng dẫn giải
Hồng nói đúng .
Vd :
(-1)+2=1
1< 2 và > -1
Bài 61 (Sách bài tập - tập 1 - trang 75)
Điền số thích hợp vào ô trống :
| \(a\) | 1 | -5 | ||
| \(-a\) | 23 | 0 | ||
| \(\left|a\right|\) |
Hướng dẫn giải
| 1 | - 23 | -5 | 0 | |
| -1 | 23 | 5 | 0 | |
| 1 | 23 | 5 | 0 |
Bài 57 (Sách bài tập - tập 1 - trang 74)
Tính :
a) \(248+\left(-12\right)+2064+\left(-236\right)\)
b) \(\left(-298\right)+\left(-300\right)+\left(-302\right)\)
Hướng dẫn giải
a)=\(\left(248-12-236\right)+2064\)
=\(0+2064=2064\)
b)=\(\left[\left(-298\right)+\left(-302\right)\right]+\left(-300\right)\)
=\(\left(-500\right)+\left(-300\right)\)
=\(-800\)
Bài 68 - Luyện tập (Sách bài tập - tập 1 - trang 76)
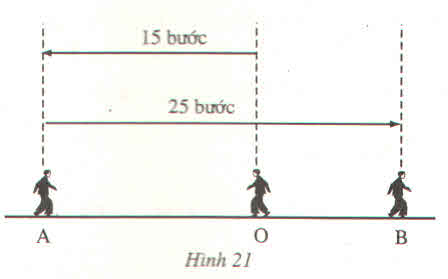
Hình 21 biểu diễn một người đi từ O đến A rồi quay về B. Đặt một bài toán phù hợp với hình 21 ?
Hướng dẫn giải
Có thể đặt một bài toán như sau:
Một người bước từ O về phía A 15 bước rồi quay lại bước về phía B 25 bước. Hỏi người đó cách điểm đứng ban đầu O bao nhiêu bước?
Bài 63 (Sách bài tập - tập 1 - trang 75)
Đố :
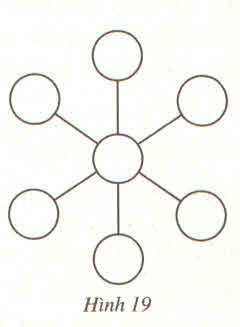
Điền các số \(-1,-2,-3,-4,5,6,7\) vào các ô tròn trong hình 19 (mỗi số vào một ô) sao cho tổng của ba số "thẳng hàng" bất kì đều bằng 0
Hướng dẫn giải
Trước hết ta cần nhận xét:
\(\left(-1\right)+\left(-2\right)+\left(-3\right)+\left(-4\right)+5+6+7=8\)
Mặt khác, tổng của ba bộ số "thẳng hàng" bằng 0 nên ta có tổng của sáu số xung quanh và ba số đứng giũa cũng bằng 0.
Từ đó suy ra: Số đứng giữa + số đứng giữa +8 = 0, nên số đứng giữa = -4.
Từ đó, ta có cách điền như hình 19 dưới đây
Bài 60 (Sách bài tập - tập 1 - trang 75)
Tính :
a) \(5+\left(-7\right)+9+\left(-11\right)+13+\left(-15\right)\)
b) \(\left(-6\right)+8+\left(-10\right)+12+\left(-14\right)+16\)
Hướng dẫn giải
a)
\(5+\left(-7\right)+9+\left(-11\right)+13+\left(-15\right)\)
\(=\left[5+\left(-7\right)\right]+\left[9+\left(-11\right)\right]+\left[13+\left(-15\right)\right]\)
\(=\left(-2\right)+\left(-2\right)+\left(-2\right)=-6\)
b)
\(\left(-6\right)+8+\left(-10\right)+12+\left(-14\right)+16\)
\(=\left[\left(-6\right)+8\right]+\left[\left(-10\right)+12\right]+\left[\left(-14\right)+16\right]\)
\(=2+2+2=6\)
Bài 72 - Luyện tập (Sách bài tập - tập 1 - trang 77)
Đố :

Điền các số \(0,1,-1,2,-2,3,-3,4,-4\) vào các ô ở hình vuông (mỗi số một ô) sao cho tổng của ba số trên hàng ngang, hàng dọc, đường chéo đều bằng 0
Hướng dẫn giải
Bài 6.1 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 75)
Điền Đ (đúng) hoặc S (sai) trong các phát biểu sau :
| Các phát biểu | Đ/S |
| a) Nếu tổng hai số tự nhiên bằng 0 thì cả hai số tự nhiên đó đều bằng 0 | |
| b) Nếu tổng hai số nguyên bằng 0 thì cả hai số nguyên đó đều bằng 0 | |
| c) Tổng của nhiều số nguyên âm cũng là một số nguyên âm có giá trị tuyệt đối bằng tổng các giá trị tuyệt đối của các số đó | |
| d) Giá trị tuyệt đối của tổng nhiều số nguyên bằng tổng các giá trị tuyệt đối của các số đó |
Hướng dẫn giải
a) Đ
b) S
c) Đ
d) S
Bài 66 - Luyện tập (Sách bài tập - tập 1 - trang 76)
Tính nhanh :
a) \(465+\left[57+\left(-465\right)+\left(-38\right)\right]\)
b) Tổng của tất cả các số nguyên có giá trị tuyệt đối nhỏ hơn hoặc bằng 15.
Hướng dẫn giải
a) 465 + [ 57 + ( -465) + ( -38 ) ]
= 465 + 57 + ( -465) + ( -38 )
=465 + ( - 465) + 57 + ( -38 )
= 0 + 19
= 19
b) Theo đầu đề bài ta có tổng:
(-15 ) + (-14) + (-13) + ... + 13 + 14 + 15
= [( -15 ) + 15] + [( -14) + 14 ]+ .... + [(-1) + 1] + 0
= 0
Bài 71 - Luyện tập (Sách bài tập - tập 1 - trang 77)
Hãy nhận xét sự thay đổi (tăng, giảm) của các số trong mỗi dãy số sau và viết hai số tiếp theo của mỗi dãy số đó. Mỗi dãy số mới có 5 số, hãy tính tổng của mỗi dãy số đó
a) \(6,1,-4,....\)
b) \(-13,-6,1,....\)
Hướng dẫn giải
a) Ta thấy: 6 - 5 = 1 ; 1 - 5 = -4
Nên 2 số tiếp theo là -9; -14
b) -13 + 7 = -6 ; -6 + 7 = 1
Vậy 2 số tiếp theo là 8; 15
Bài 58 (Sách bài tập - tập 1 - trang 75)
Tìm tổng tất cả các số nguyên \(x\) thỏa mãn :
a) \(-6< x< 5\)
b) \(-9< x< 9\)
Hướng dẫn giải
a)\(x\in\left\{-5;-4;...4\right\}\)
Vậy tổng \(x=-5+\left(-4+4\right)+...+\left(-1+1\right)=-5+0=-5\)
b)\(x\in\left\{-8;-7;...;8\right\}\)
Vậy tổng \(x=\left(-8+8\right)\left(-7+7\right)+...+\left(-1+1\right)=0\)
Bài 59 (Sách bài tập - tập 1 - trang 75)
Chiếc diều của bạn Sơn bay ở độ cao 7m (so với mặt đất). Sau một lúc, độ cao của chiếc diều tăng thêm 3 m, rồi sau đó giảm đi 4 mét. Hỏi chiếc diều ở độ cao bao nhiêu mét (so với mặt đất) sau hai lần thay đổi độ cao ?
Hướng dẫn giải
Sau 2 lần thay đổi , chiếc diều bay ở độ cao :
7 + 3 - 4 = 6 ( m )
Bài 6.3 (Sách bài tập - tập 1 - trang 77)
Tính giá trị của biểu thức :
\(x+255,\) biết \(x=\left(-47\right)+45\)
Hướng dẫn giải
B1:Thay x vào biểu thức, ta đc:
(-47)+45+225
B2: Tính
(-47)+45+225
=(-2)+225
=223
Bài 67 - Luyện tập (Sách bài tập - tập 1 - trang 76)
Hai ôtô cùng xuất phát từ O đi về phía A hoặc B (h.20).

Ta quy ước chiều từ O đến B là chiều dương và chiều ngược lại từ O đến A là chiều âm. Hỏi sau một giờ hai ôtô cách nhau bao nhiêu km nếu vận tốc của chúng lần lượt là :
a) 40km/h và 30 km/h
b) 40km/h và -30km/h
Hướng dẫn giải
Bài làm :
a) Vì vận tốc 2 ô tô đều là dương nên hai ô tô đều đi về phía B ( chiều từ O đến B là chiều dương ) . Nên sau 1 giờ khoảng cách mà hai ô tô cách nhau chính là hiệu quãng đường mà hai ô tô đi được .
Áp dụng công thức : Quãng đường = vận tốc x thời gian
Quãng đường mà ô tô thứ nhất đi được là :
40 . 1 = 40 (km)
Quãng đường mà ô tô thứ hai đi được là
30 . 1 = 30 (km)
Sau một giờ hai ô tô cách nhau là :
40 - 30 = 10 (km)
b) Vì :
+ Vận tốc ô tô thứ nhất = 40 km/h ( vận tốc dương ) nên có chiều đi từ O đến B .
+ Vận tốc ô tô thứ hai = -30 km/h ( vận tốc âm ) nên có chiều đi từ O đến A
\(\Rightarrow\) Hai ô tô đi ngược chiều nhau
Vì 2 ô tô đi ngược chiều nhau nên khoảng cách hai ô tô sau một giờ chính là tổng quãng đường mà hai ô tô đã đi được .
Áp dụng công thức : Quãng đường = vận tốc x thời gian
Quãng đường mà ô tô thứ nhất đi được là :
40 . 1 = 40 (km)
Quãng đường mà ô tô thứ hai đi được là
30 . 1 = 30 (km)
Khoảng cách hai ô tô sau một giờ là :
40 + 30 = 70 (km)




