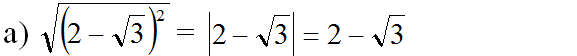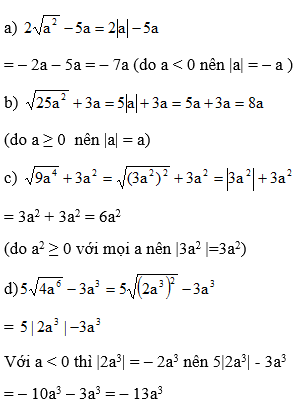Căn thức bậc hai và hằng đẳng thức căn bậc hai của bình phương

Lý thuyết

Bài 6 (SGK trang 10)

Với giá trị nào của a thì mỗi căn thức sau có nghĩa:

a. \(\sqrt{\dfrac{a}{3}}\);             b. \(\sqrt{-5a};\)               c. \(\sqrt{4-a};\)                    d. \(\sqrt{3a+7}?\)

Hướng dẫn giải

a, \(a\ge0\)

b, a \(\le0\)

c, \(a\le4\)

d, \(a\ge-\dfrac{7}{3}\)

Bài 7 (SGK trang 10)

Tính:

a. \(\sqrt{\left(0,1\right)^2};\)             b. \(\sqrt{\left(-0,3\right)^2};\)              c. \(-\sqrt{\left(-1,3\right)^2};\)           d. \(-0,4\sqrt{\left(-0,4\right)^2}.\)

Hướng dẫn giải

a, 0,1

b,0,3

c,-1,3

d,-0,16

Bài 8 (SGK trang 10)

Rút gọn các biểu thức sau:

a. \(\sqrt{\left(2-\sqrt{3}\right)^2};\)

b. \(\sqrt{\left(3-\sqrt{11}\right)^2};\)

c. \(2\sqrt{a^2}\) với \(a\ge0;\)

d. \(3\sqrt{\left(a-2\right)^2}\) với a < 2.

Hướng dẫn giải

Bài 9 (SGK trang 11)

Tìm x, biết:

a. \(\sqrt{x^2}=7;\)

b. \(\sqrt{x^2}=\left|-8\right|;\)

c. \(\sqrt{4x^2}=6;\)

d. \(\sqrt{9x^2}=\left|-12\right|.\)

Hướng dẫn giải

a. \(\sqrt{x^2}=7\Leftrightarrow\left|x\right|=7\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-7\end{matrix}\right..\)

b. \(\sqrt{x^2}=\left|-8\right|\Leftrightarrow\left|x\right|=8\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right..\)

c. \(\sqrt{4x^2}=6\Leftrightarrow\left|2x\right|=6\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right..\)

d. \(\sqrt{9x^2}=\left|-12\right|\Leftrightarrow\left|3x\right|=12\Leftrightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right..\)

Bài 10 (SGK trang 11)

Chứng minh:

a. \(\left(\sqrt{3}-1\right)^2=4-2\sqrt{3};\)

b. \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=-1.\)

Hướng dẫn giải

a) Ta có :

4 - 2\(\sqrt{3}\) = 1 - 2.1.\(\sqrt{3}\) + 3 = 1 - 2.1.\(\sqrt{3}\) + (\(\sqrt{3}\))² = (1 - \(\sqrt{3}\))²= (\(\sqrt{3}\) - 1)²

b) Áp dụng câu a ta có:

\(\sqrt{4-2\sqrt{3}}\) - \(\sqrt{3}\) = \(\sqrt{\left(\sqrt{3}-1\right)^2}\) - \(\sqrt{3}\) = (\(\sqrt{3}\) - 1) -\(\sqrt{3}\)

= \(\sqrt{3}\) - 1 - \(\sqrt{3}\) = -1

Bài 11 (SGK trang 11)

Tính:

a. \(\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49};\)

b. \(36:\sqrt{2.3^2.18}-\sqrt{169};\)

c. \(\sqrt{\sqrt{81}};\)

d. \(\sqrt{3^2+4^2}.\)

Hướng dẫn giải

a) \(\sqrt{16}\cdot\sqrt{25}+\sqrt{196}:\sqrt{49}\)

\(=\sqrt{16\cdot25}+\sqrt{196:49}\)

\(=20+2=22\)

b) \(36:\sqrt{2\cdot3^2\cdot18}-\sqrt{169}\)

\(=36:\sqrt{324}-\sqrt{169}\)

\(=36:18-13=2-13=-11\)

c) \(\sqrt{\sqrt{81}}\)

\(=\sqrt{9}=3\)

d) \(\sqrt{3^2+4^2}\)

\(=\sqrt{9+16}=\sqrt{25}=5\)

Bài 12 (SGK trang 11)

Tìm x để mỗi căn thức sau có nghĩa:

a. \(\sqrt{2x+7};\)       b. \(\sqrt{-3x+4};\)          c. \(\sqrt{\dfrac{1}{-1+x}};\)       d. \(\sqrt{1+x^2}.\)

Hướng dẫn giải

a) \(\sqrt{2x+7}\) có nghĩa khi \(2x+7\ge0\) \(\Leftrightarrow\) \(2x\ge-7\) \(\Leftrightarrow\) \(x\ge\dfrac{-7}{2}\)

b) \(\sqrt{-3x+4}\) có nghĩa khi \(-3x+4\ge0\) \(\Leftrightarrow\) \(-3x\ge-4\) \(\Leftrightarrow\) \(x\le\dfrac{4}{3}\)

c) \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi \(\dfrac{1}{-1+x}>0\) \(\Leftrightarrow\) \(-1+x>0\) \(\Leftrightarrow\) \(x>1\)

\(\sqrt{1+x^2}\) ta có \(1+x^2>0\forall x\) \(\Rightarrow\) căn thức luôn có nghĩa\(\forall x\)

Bài 13 (SGK trang 11)

Rút gọn các biểu thức sau:

a. \(2\sqrt{a^2}-5a\) với a < 0;               b. \(\sqrt{25a^2}+3a\) với \(a\ge0;\)

c. \(\sqrt{9a^4}+3a^2;\)                             d. \(5\sqrt{4a^6}-3a^3\) với a < 0.

Hướng dẫn giải

Bài 14 (SGK trang 11)

Phân tích thành nhân tử:

a. x² - 3;                                                    b. x² - 6;

c. \(x^2+2\sqrt{3}x+3;\)                                   d. \(x^2-2\sqrt{5}x+5.\)

 

Hướng dẫn giải

a) x²-3=(x-\(\sqrt{3}\))(x+\(\sqrt{3}\))

b) x²-6=(x-\(\sqrt{6}\))(x+\(\sqrt{6}\))

c) x²+2\(\sqrt{3}\)x +3 = x² + 2.x.\(\sqrt{3}\) + (\(\sqrt{3}\))²= (x+\(\sqrt{3}\))²=(x+\(\sqrt{3}\))(x+\(\sqrt{3}\)).

d) x²-2\(\sqrt{5}\) x+ 5 = x² - 2.x.\(\sqrt{5}\) + (\(\sqrt{5}\))² = (x-\(\sqrt{5}\))²= (x-\(\sqrt{5}\))(x-\(\sqrt{5}\)).

Bài 15 (SGK trang 11)

Giải các phương trình sau:

a.   \(x^2-5=0;\)                      b. \(x^2-2\sqrt{11}x+11=0.\)

Hướng dẫn giải

a, \(x^2-5=0\Leftrightarrow\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)=0\Leftrightarrow x=\pm\sqrt{5}\)

b, \(x^2-2\sqrt{11}+11=0\Leftrightarrow\left(x-\sqrt{11}\right)^2=0\Leftrightarrow x=\sqrt{11}\)