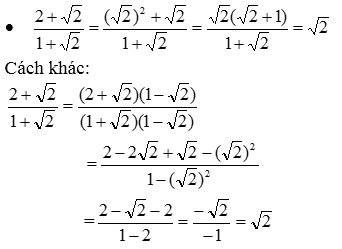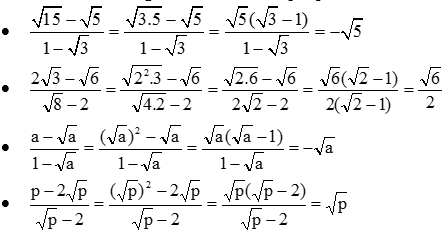Biến đối đơn giản biểu thức chứa căn bậc hai (Tiếp theo)

Mục lục

* * * * *

Bài 48 (SGK trang 29)

Khử mẫu của biểu thức lấy căn:

$\sqrt{\dfrac{1}{600}};\sqrt{\dfrac{11}{540}};\sqrt{\dfrac{3}{50}};\sqrt{\dfrac{5}{98}};\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}.$

Hướng dẫn giải

$\sqrt{\frac{1}{600}}=\frac{\sqrt{6}}{60}$ ;

$\sqrt{\frac{11}{540}}=\frac{\sqrt{165}}{90};$

$\sqrt{\frac{3}{50}}=\frac{\sqrt{6}}{10};$

$\sqrt{\frac{(1-\sqrt{3})^{2}}{27}}=\frac{(\sqrt{3}-1)\sqrt{3}}{9}.$

Bài 49 (SGK trang 29)

Khử mẫu của biểu thức lấy căn:

$ab\sqrt{\dfrac{a}{b}};\dfrac{a}{b}\sqrt{\dfrac{b}{a}};\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}};\sqrt{\dfrac{9a^3}{36b}};3xy\sqrt{\dfrac{2}{xy}}.$

(Giả thiết các biểu thức có nghĩa).

Hướng dẫn giải

$\sqrt{\frac{a}{b}}$ có nghĩa khi $\frac{a}{b}\geq 0$ và $\sqrt{\frac{a}{b}}=\frac{\sqrt{ab}}{\left | b \right |}.$
Nếu $a\geq 0, b> 0$ thì $ab\sqrt{\frac{a}{b}}=a\sqrt{ab}.$
Nếu $a<0, b<0$ thì $ab\sqrt{\frac{a}{b}}=-a\sqrt{ab}.$
Tương tự như vậy ta có: $\frac{a}{b}\sqrt{\frac{b}{a}}=\frac{\sqrt{ba}}{b}.$
Nếu $a> 0, b> 0$ thì $\frac{a}{b}\sqrt{\frac{b}{a}}=\frac{a}{b}\frac{\sqrt{ba}}{\left | a \right |}.$
Nếu $a<0, b<0$ thì $\frac{a}{b}\sqrt{\frac{b}{a}}=-\frac{\sqrt{ba}}{b}.$
Ta có: $\sqrt{\frac{1}{b}+\frac{1}{b^{2}}}=\sqrt{\frac{b+1}{b^{2}}}=\frac{\sqrt{b+1}}{\left | b \right |}.$
Điều kiện để căn thức có nghĩa là $b+1\geq 0$ hay $b\geq -1.$ Do đó:
Nếu b>0 thì $\sqrt{\frac{1}{b}+\frac{1}{b^{2}}}=\frac{\sqrt{b+1}}{ b }.$
Nếu $-1\leq b< 0$ thì $\sqrt{\frac{1}{b}+\frac{1}{b^{2}}}=-\frac{\sqrt{b+1}}{b}.$
Điều kiện để $\sqrt{\frac{9a^{3}}{36b}}$ có nghĩa là $\frac{9a^{3}}{36b}\geq 0$ hay $\frac{a}{b}\geq 0$
Cách 1. $\sqrt{\frac{9a^{3}}{36b}}=\sqrt{\frac{a^{3}}{4b}}=\frac{\sqrt{4a^{3}b}}{4\left | b \right |}=\frac{\sqrt{4a^{2}\cdot ab}}{4\left | b \right |}=\frac{2\left | a \right |\sqrt{ab}}{4b}.$
= $\frac{1}{2}\left | \frac{a}{b} \right |\sqrt{ab}=\frac{a\sqrt{ab}}{2b}.$
Cách 2. Biến mẫu thành một bình phương rồi áp dụng quy tắc khai phương một thương: $\sqrt{\frac{9a^{3}}{36b}}=\sqrt{\frac{a^{3}b}{4b^{2}}}=\frac{\sqrt{a^{3}b}}{\sqrt{ab^{2}}}=\frac{\left | a \right |\sqrt{ab}}{2\left | b \right |}=\frac{1}{2}\left | \frac{a}{b} \right |\sqrt{ab}=\frac{a\sqrt{ab}}{2b}.$
Điều kiện để $\sqrt{\frac{2}{xy}}$ có nghĩa là $\frac{2}{xy}\geq 0$ hay xy>0.
Do đó

$3xy\sqrt{\frac{2}{xy}}=3xy\frac{\sqrt{2xy}}{\left | xy \right |}=3xy\frac{\sqrt{2xy}}{xy}=3\sqrt{2xy}.$

Bài 50 (SGK trang 30)

Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:

$\dfrac{5}{\sqrt{10}};\dfrac{5}{2\sqrt{5}};\dfrac{1}{3\sqrt{20}};\dfrac{2\sqrt{2}+2}{5\sqrt{2}};\dfrac{y+b\sqrt{y}}{b.\sqrt{y}}.$

Hướng dẫn giải

Nhat Linh bị nhầm câu cuối:

$\dfrac{y+b\sqrt{y}}{b.\sqrt{y}}=\dfrac{y\sqrt{y}+b.y}{b.y}=\dfrac{\sqrt{y}+b}{b}.$

Bài 51 (SGK trang 30)

Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:

$\dfrac{3}{\sqrt{3}+1};\dfrac{2}{\sqrt{3}-1};\dfrac{2+\sqrt{3}}{2-\sqrt{3}};\dfrac{b}{3+\sqrt{b}};\dfrac{p}{2\sqrt{p}-1}.$

Hướng dẫn giải

$\frac{3(\sqrt{3}-1)}{2}; \sqrt{3}+1; 7+4\sqrt{3};\frac{b(3-\sqrt{b})}{9-b}; \frac{p(2\sqrt{p}+1)}{4p-1}.$

Bài 52 (SGK trang 30)

Trục căn thức ở mẫu và giả thiết các biểu thức đều có nghĩa:

$\dfrac{2}{\sqrt{6}-\sqrt{5}};\dfrac{3}{\sqrt{10}+\sqrt{7}};\dfrac{1}{\sqrt{x}-\sqrt{y}};\dfrac{2ab}{\sqrt{a}-\sqrt{b}}.$

Hướng dẫn giải

ĐS: $2(\sqrt{6}+\sqrt{5}); \sqrt{10}-\sqrt{7};\frac{\sqrt{x}+\sqrt{y}}{x-y}; \frac{2ab(\sqrt{a}+\sqrt{b})}{a-b}.$

Bài 53 (SGK trang 30)

Rút gọn các biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa):

a. $\sqrt{18\left(\sqrt{2}-\sqrt{3}\right)^2};$

b. $ab\sqrt{1+\dfrac{1}{a^2b^2}};$

c. $\sqrt{\dfrac{a}{b^3}+\dfrac{a}{b^4}};$

d. $\dfrac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.$

Hướng dẫn giải

a) ĐS: $3(\sqrt{6}-2)$ .

b) ĐS: Nếu $ab> 0$ thì $ab\sqrt{1+\frac{1}{a^{2}b^{2}}}=\sqrt{{a^{2}b^{2}+1}}.$

Nếu ab

c) ĐS: $\frac{\sqrt{ab+a}}{b^{2}}.$

d) $\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\frac{(a+\sqrt{ab})(\sqrt{a}-\sqrt{b})}{a-b}=\frac{a\sqrt{a}-a\sqrt{b}+\sqrt{ab}\sqrt{a}-\sqrt{ab}\sqrt{b}}{a-b}$

$=\frac{a\sqrt{a}-a\sqrt{b}+\sqrt{a^{2}b}-\sqrt{ab^{2}}}{a-b}=\frac{a\sqrt{a}-a\sqrt{b}+a\sqrt{b}-b\sqrt{a}}{a-b}$

$=\frac{(a-b)\sqrt{a}}{a-b}=\sqrt{a}.$

Nhận xét. Nhận thấy rằng để $sqrt{a}$ có nghĩa thì $ageq 0.$ Do đó $a=(\sqrt{a})^{2}$ . Vì thế có thể phân tích tử thành nhân tử.

$\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\frac{(\sqrt{a})^{2}+\sqrt{a}.\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}(\sqrt{a}+\sqrt{b})}{\sqrt{a}+\sqrt{b}}=\sqrt{a}.$

Luyện tập - Bài 54 (SGK trang 30)

Rút gọn các biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa)

$\dfrac{2+\sqrt{2}}{1+\sqrt{2}}$ $\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}$ $\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}$ $\dfrac{a-\sqrt{a}}{1-\sqrt{a}}$ $\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}$

Hướng dẫn giải

Để học tốt Toán 9 | Giải bài tập Toán 9

Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.

Để học tốt Toán 9 | Giải bài tập Toán 9

Luyện tập - Bài 55 (SGK trang 30)

Phân tích thành nhân tử (với a, b, x, y là các số không âm)

a) $ab+b\sqrt{a}+\sqrt{a}+1$

b) $\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}$

Hướng dẫn giải

a. $ab+b\sqrt{a}+\sqrt{a}+1=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)$

b. $\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)+\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)=\left(\sqrt{x}-\sqrt{y}\right)\left(x+2\sqrt{xy}+y\right)=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)^2$

Luyện tập - Bài 56 (SGK trang 30)

Sắp xếp theo thứ tự tăng dần :

a) $3\sqrt{5};2\sqrt{6};\sqrt{29};4\sqrt{2}$

b) $6\sqrt{2};\sqrt{38};3\sqrt{7};2\sqrt{14}$

Hướng dẫn giải

a. $3\sqrt{5}=\sqrt{45}$ ; $2\sqrt{6}=\sqrt{24}$ ; $4\sqrt{2}=\sqrt{32}$

Vì 24 < 29 < 32 < 45 nên $\sqrt{24}< \sqrt{29}< \sqrt{32}< \sqrt{45}$

Hay $2\sqrt{6}< \sqrt{29}< 4\sqrt{2}< 3\sqrt{5}$

b. $6\sqrt{2}=\sqrt{72}$ ; $3\sqrt{7}=\sqrt{63}$ ; $2\sqrt{14}=\sqrt{56}$

Vì 38 < 56 < 63 < 72 nên $\sqrt{38}< \sqrt{56}< \sqrt{63}< \sqrt{72}$

Hay $\sqrt{38}< 2\sqrt{14}< 3\sqrt{7}< 6\sqrt{2}$

Luyện tập - Bài 57 (SGK trang 30)

$\sqrt{25x}-\sqrt{16x}=9$ khi $x$ bằng :

(A) 1 (B) 3 (C) 9 (D) 81

Hãy chọn câu trả lời đúng

Hướng dẫn giải

$\sqrt{25x}-\sqrt{16x}=9$ khi $x$ bằng :

(A) 1 (B) 3 (C) 9 (D) 81

Có thể bạn quan tâm

Hỏi đáp

MÔN HỌC

Biến đối đơn giản biểu thức chứa căn bậc hai (Tiếp theo)

Bài 48 (SGK trang 29)

Hướng dẫn giải

Bài 49 (SGK trang 29)

Hướng dẫn giải

Bài 50 (SGK trang 30)

Hướng dẫn giải

Bài 51 (SGK trang 30)

Hướng dẫn giải

Bài 52 (SGK trang 30)

Hướng dẫn giải

Bài 53 (SGK trang 30)

Hướng dẫn giải

Luyện tập - Bài 54 (SGK trang 30)

Hướng dẫn giải

Luyện tập - Bài 55 (SGK trang 30)

Hướng dẫn giải

Luyện tập - Bài 56 (SGK trang 30)

Hướng dẫn giải

Luyện tập - Bài 57 (SGK trang 30)

Hướng dẫn giải

Có thể bạn quan tâm

Có thể bạn quan tâm