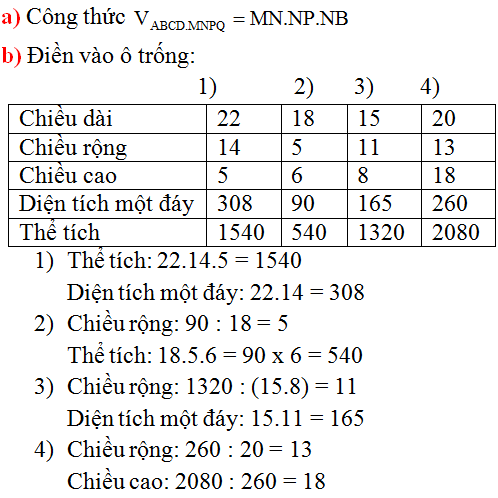
Thể tích hình hộp chữ nhật
Bài 10 (Sgk tập 2 - trang 103)
1) Gấp hình 87 a theo các nét đã chỉ ra thì có được 1 hình hộp chữ nhật hay không ?
2) Kí hiệu các đỉnh hình hộp gấp được như hình 87b
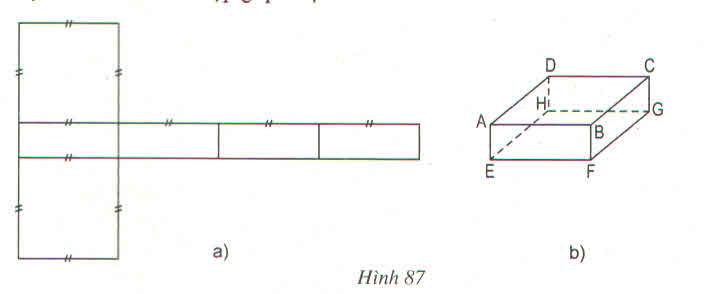
a) Đường thẳng BF vuông góc với những mặt phẳng nào ?
b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau, vì sao ?
Hướng dẫn giải
Lời giải
1. Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và (DHEA)
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H.
Bài 11 (Sgk tập 2 - trang 104)
a) Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với 3, 4, 5 và thể tích của hình hộp này là \(480cm^3\)
b) Diện tích toàn phần của một hình lập phương là \(486m^2\). Thể tích của nó là bao nhiêu ?
Hướng dẫn giải
Gọi a, b, c là ba kích thước của hình hộp chữ nhật.
Bài 12 (Sgk tập 2 - trang 104)
A, B, C và D là những đỉnh của hình hộp chữ nhật cho ở hình 88. Hãy điền số thích hợp vào các ô trống ở bảng sau :

Kết quả bài 12 minh họa công thức quan trọng sau :
\(DA=\sqrt{AB^2+BC^2+CD^2}\)
Hướng dẫn giải
Bài 13 (Sgk tập 2 - trang 104)
a) Viết công thức tính thể tích của hình hộp chữ nhật ABCD.MNPQ (h.89)
b) Điền số thích hợp vào các ô trống ở bảng sau :

Hướng dẫn giải
Luyện tập - Bài 14 (Sgk tập 2 - trang 104)
Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 l thì mực nước của bể cao 0,8m
a) Tính chiều rộng của bể nước
b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đẩy bể
Hỏi bể cao bao nhiêu mét ?
Hướng dẫn giải
a) Thể tích nước đổ vào:
120 x 20 = 2400 (l) = 2,4 (m3)
Chiều rộng của bể nước:
2,4 : (2 x 0,8) = 1,5(m)
b) Thể tích của hồ nước:
2400 + 60 x 20 = 3600 (l) = 3,6 (m3)
Chiều cao của hồ nước:
3,6 : (2 x 1,5) = 1,2 (m)
Luyện tập - Bài 15 (Sgk tập 2 - trang 105)
Một cái thùng hình lập phương, cạnh 7dm, có chứa nước với độ sâu của nước là 4dm. Người ta thả 25 viên gạch có chiều dài 2dm, chiều rộng 1dm và chiều cao 0,5 dm vào thùng. Hỏi nước trong thùng dâng lên cách miệng thùng bao nhiêu dm ? (Giả thiết toàn bộ gạch ngập trong nước và chúng hút nước không đáng kể)
Hướng dẫn giải
Thể tích của nước trong thùng:
7 x 7 x 4 = 196 (dm3)
Thể tích của 25 viên gạch:
25 x (2 x 1 x 0,5) = 25 (dm3)
Thể tích của nước và gạch:
196 + 25 = 221 (dm3)
Nước trong thùng dâng lên cách miệng thùng là:
(343 – 221) : (7 x 7) \(\approx\)2,49 (dm)
Luyện tập - Bài 16 (Sgk tập 2 - trang 105)
Thùng chứa của một xe chở hàng đông lạnh có dạng như hình 90. Một số mặt hàng là những hình chữ nhật, chẳng hạn (ABKI), (DCC'D'),...Quan sát hình và trả lời các câu hỏi sau :
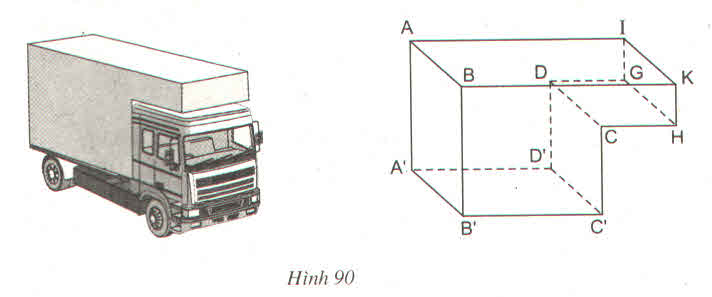
a) Những đường thẳng nào song song với mặt phẳng (ABKI) ?
b) Những đường thẳng nào vuông góc với mặt phẳng (DCC'D') ?
c) Mặt phẳng (A'D'C'B') có vuông góc với mặt phẳng (DCC'D') hay không ?
Hướng dẫn giải
a) Những đường thẳng song song với mặt phẳng (ABKI) là DG; CH; A'D'; B'C'; A'B'; D'C'; DC; JH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') => (A'B'C'D') \(\perp\) (CDD'C')
Luyện tập - Bài 17 (Sgk tập 2 - trang 105)
Cho hình hộp chữ nhật ABCD.EFGH (h.91)

a) Kể tên các đường thẳng song song với mp (EFGH)
b) Đường thẳng AB song song với những mặt phẳng nào ?
c) Đường thẳng AD song song với những đường thẳng nào ?
Hướng dẫn giải
a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳn AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH
Luyện tập - Bài 18 (Sgk tập 2 - trang 105)
Đố :
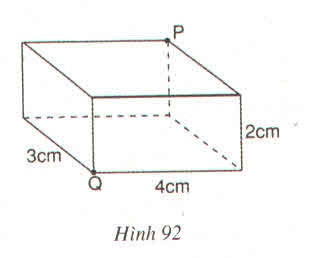
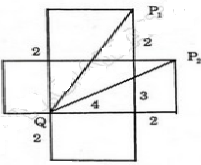
Các kích thước của một hình hộp chữ nhật là 4cm, 3cm, 2cm. Một con kiến bò theo mặt phẳng của hình hộp đó từ Q đến P
a) Hỏi con kiến bò theo đường nào ngắn nhất ?
b) Độ dài ngắn nhất đó là bao nhiên cm ?
Hướng dẫn giải
Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.