Đường thẳng song song với một đường thẳng cho trước

Lý thuyết

Bài 130 (Sách bài tập - trang 96)

Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bởi hai đường chéo ?

Hướng dẫn giải

Gọi O là giao điểm của hai đường chéo AC và BD.

AC = BD (tính chất hình chữ nhật)

\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)

\(AD=\dfrac{1}{2}AC\left(gt\right)\)

\(\Rightarrow OA=OD=AD\)

\(\Rightarrow\Delta OAD\) đều

\(\Rightarrow\widehat{AOD}=60^0\)

Bài 125 (Sách bài tập - trang 95)

Cho góc vuông xOy, điểm A trên tia Oy. Điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào ?

Hướng dẫn giải

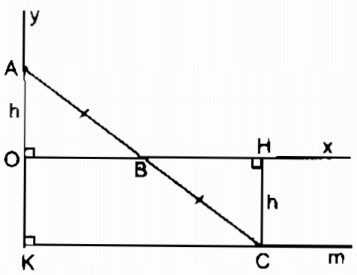
Vì điểm C đối xứng với điểm A qua điểm B ⇒ BA = BC

Kẻ CH ⊥ Ox

Xét ∆ AOB và ∆ CHB ta có :

\(\widehat{AOB}=\widehat{CHB}=90^o\)

\(BA=BC\left(cmt\right)\)

\(\widehat{ABO}=\widehat{CBH}\) ( đối đỉnh )

\(\Rightarrow\)∆ AOB = ∆ CHB (cạnh huyền, góc nhọn) ⇒ CH = AO ( 2 cạnh tương ứng )

A, O cố định ⇒ OA không đổi nên CH không đổi.

C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng OA.

Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.

Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.

Bài 131 (Sách bài tập - trang 96)

Dựng hình chữ nhật ABCD, biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng \(100^0\)  ?

Hướng dẫn giải

Cách dựng:

- Dựng ∆ OAB biết OA = OB = 2cm

\(\widehat{AOB}=100^o\)

- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm

- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm

Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng.

Bài 129* (Sách bài tập - trang 96)

Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?

Hướng dẫn giải

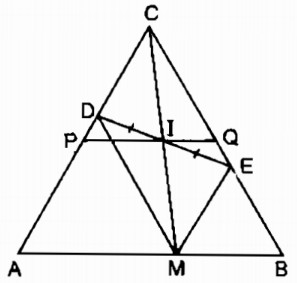
Gọi giao điểm của AD và BE là C.

∆ ABC có: (vì ∆ ADM đều)

(vì ∆ BEM đều)

Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định

⇒ ME // AC (vì có cặp góc đồng vị bằng nhau)

hay ME // DC

⇒ MD // BC (vì có cặp góc đồng vị bằng nhau)

hay MD // EC

Tứ giác CDME là hình bình hành

I là trung điểm của DE nên I là trung điểm của CM

Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH

Trong ∆ CHM ta có:

CI = IM

IK // CH

nên IK là đường trung bình của ∆ CHM ⇒ IK = CH

C cố định ⇒ CH không đổi ⇒ IK =CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng CH.

Khi M trùng với A thì I trùng trung điểm P của AC.

Khi M trùng với B thì I trùng với trung điểm Q của BC.

Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC)

Xem thêm tại: http://sachbaitap.com/cau-129-trang-96-sach-bai-tap-sbt-toan-8-tap-1-c6a8515.html#ixzz4zLYSfxii

Bài 124 (Sách bài tập - trang 95)

Cho đoạn thẳng AB. Kẻ tia Ax bất kì, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C và D kẻ các đường thẳng song song với EB. Chứng minh rằn đoạn thẳng AB bị chia thành 3 phần bằng nhau.

Hướng dẫn giải

Ta có AC = CD và CC’ // BE

CD = DE và DD’ // BE

=> CC’ // DD’ và CEBC’ là hình thang

=> CC’ là đường trung bình của tam giác ADD’

DD’ là đường trung bình của hình thang CEBC’

=> AC’ = CD’ và C’D’ = D’B => AC’ = CD’ = D’B

Bài 127 (Sách bài tập - trang 96)

Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC

a) So sánh các độ dài AM, DE

b) Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất 

Hướng dẫn giải

a)Xét tứ giác ADME có góc MDA=90(gt)

góc DAE=90(gt)

góc AEM=90(gt)

=>tứ giác ADME là hình chữ nhật

=>AM=DE

b)Kẻ AH vuông góc với BC

Ta có DE=AM>=AH

Dấu "=" xãy ra khi M trùng H

Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường cao kẻ từ A đến BC

Bài 10.2 - Bài tập bổ sung (Sách bài tập - trang 96)

Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?

Hướng dẫn giải

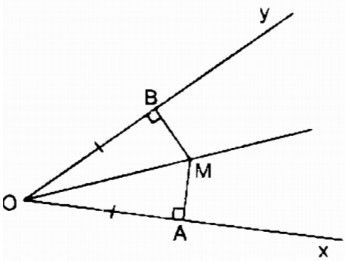
Xét hai tam giác vuông MOA và MOB:

OA = OB (gt)

OM cạnh huyền chung

Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)

\(\widehat{AOM}=\widehat{BOM}\)

A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó

Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.

Bài 10.1 - Bài tập bổ sung (Sách bài tập - trang 96)

Tập hợp giao điểm hai đường chéo của hình chữ nhật ABCD có A và B cố định là :

(A) Đường trung trực của AD

(B) Đường trung trực của AB

(C) Đường trung trực BC

(D) Đường tròn (A; AB)

Hướng dẫn giải

(B)

Bài 126 (Sách bài tập - trang 96)

Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào ?

Hướng dẫn giải

Gọi E và F lần lượt là trung điểm của AB và AC.
Ta sẽ chứng minh ba điểm E, I, F thẳng hàng.
Do E, I lần lượt là trung điểm của AB và AM nên EI là đường trung bình của tam giác ABM. Suy ra:
EI \\ BM suy ra EI // BC. (1)
Do I, F lần lượt là trung điểm của AC và AM nên IF là đường trung bình của tam giác AMC.
Suy ra: IF // MC suy ra FI // BC. (2)
Từ (1) và (2) ta có EI và FI cùng song song với BC nên ba điểm E, F, I thẳng hàng.
Do E, F cố định nên khi M khi di chuyển trên BC thì I di chuyển trên EF.

Bài 128 (Sách bài tập - trang 96)

Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào ?

Hướng dẫn giải

Bài 10.3 - Bài tập bổ sung (Sách bài tập - trang 96)

Xét các hình bình hành ABCD có cạnh AD cố định, cạnh AB = 2cm. Gọi I là giao điểm của AC và BD. Điểm I chuyển động trên đường nào ?

Hướng dẫn giải

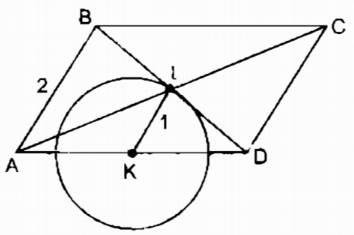
Gọi K là trung điểm của cạnh AD.

ta có AD cố định nên điểm K cố định.

Trong ∆ ABD ta có:

IB = ID (tính chất hình bình hành)

KA = KD (theo cách vẽ)

nên KI là đường trung bình của ∆ ABD

⇒ KI = \(\dfrac{1}{2}AB=\dfrac{1}{2}.2\) = 1 (cm) (tính chất đường trung bình của tam giác)

B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K ; 1 cm)