Ôn tập Tam giác
Lý thuyết
Mục lục
* * * * *
Bài 104 (Sách bài tập - tập 1 - trang 152)
Cho tam ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho \(DB=EC< \dfrac{1}{2}DE\)
a) Tam giác ABC là tam giác gì ? Chứng minh điều gì ?
b) Kẻ \(BM\perp AD,CN\perp AE\). Chứng minh rằng BM = CN
c) Gọi I là giao điểm của MB và NC. Tam giác IBC là tam giác gì ? Chứng minh điều đó
d) Chứng minh rằng AI là tia phân giác của góc BAC
Hướng dẫn giải
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
=> \(\Delta BMD=\Delta CNE\left(ch-gn\right)\)
=> BM = CN
c) Ta có :
\(\widehat{MBD}=\widehat{NCE}\) ( \(\Delta BMD=\Delta CNE\) )
mà \(\widehat{MBD}=\widehat{IBC},\widehat{NCE}=\widehat{ICB}\) ( 2 góc đối đỉnh )
=> \(\widehat{IBC}=\widehat{ICB}\)
=> Tam giác IBC cân tại I
d) \(\Delta IAB=\Delta IAC\left(c.c.c\right)\)
=> \(\widehat{IAB}=\widehat{IAC}\)
=> AI là tia phân giác của góc BAC
Bài 108 (Sách bài tập - tập 1 - trang 152)
Bạn Mai vẽ tia phân giác của một góc như sau : Đánh dấu trên hai cạnh của góc bốn đoạn thẳng bằng nhau : OA = AB = OC = CD
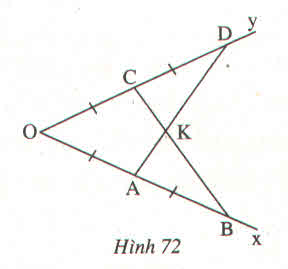
Kẻ các đoạn thẳng AD, BC, chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O
Hướng dẫn : Chứng minh rằng :
a) \(\Delta OAD=\Delta OCB\)
b) \(\Delta KAB=\Delta KCD\)
Hướng dẫn giải
Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)
Bài 106 (Sách bài tập - tập 1 - trang 152)
Tìm các tam giác bằng nhau trên hình 70 ?
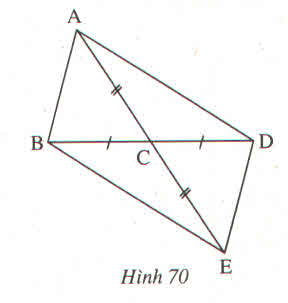
Hướng dẫn giải
Các tam giác bằng nhau:
\(\Delta ABC=\Delta EDC\left(c-g-c\right)\)
\(\Delta ACD=\Delta ECB\left(c-g-c\right)\)
\(\Delta ABD=\Delta EDB\left(c-c-c\right)\)
\(\Delta ABE=\Delta EDA\left(c-c-c\right)\).
Bài 107 (Sách bài tập - tập 1 - trang 152)
Tìm các tam giác cân trên hình 71 ?
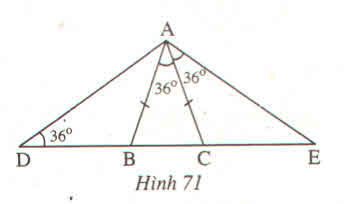
Hướng dẫn giải
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
Bài 109 (Sách bài tập - tập 1 - trang 152)
Cho tam giác ABC cân tại A, kẻ \(BH\perp AC\). Gọi D là một điểm thuộc cạnh đáy BC. Kẻ \(DE\perp AC,DF\perp AB\)
Chứng minh rằng \(DE+DF=BH\)
Hướng dẫn giải
Kẻ DK \(\perp\) BH
Ta có: DK \(\perp\)BH
AC \(\perp\) BH
\(\Rightarrow\)DK // AC
\(\Rightarrow\) \(\widehat{BDK}=\widehat{C}\) (hai góc đồng vị) (1)
Vì \(\Delta ABC\) cân tại A \(\Rightarrow\) \(\widehat{DBF}=\widehat{C}\) (2)
Từ (1) và (2) suy ra: \(\widehat{BDK}=\widehat{DBF}\)
Xét hai tam giác vuông BDK và DBF có:
BD: cạnh huyền chung
\(\widehat{BDK}=\widehat{DBF}\) (cmt)
Vậy: \(\Delta BDK=\Delta DBF\left(ch-gn\right)\)
Suy ra: BK = DF (hai cạnh tương ứng) (3)
Ta lại có DE // KH, DK // EH nên chứng minh được: DE = KH (4)
Từ (3) và (4) suy ra: DE + DF = KH + BK = BH (đpcm).
Bài 103 (Sách bài tập - tập 1 - trang 152)
Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh rằng CD là đường trung trục của AB ?
Hướng dẫn giải
Xét hai tam giác ACD và BCD có:
AC = BC (gt)
AD = BD (gt)
CD: cạnh chung
Vậy: \(\Delta ACD=\Delta BCD\left(c-c-c\right)\)
Suy ra: \(\widehat{C_1}=\widehat{C_2}\) (hai góc tương ứng)
Xét hai tam giác ACH và BCH có:
AC = BC (gt)
\(\widehat{C_1}=\widehat{C_2}\) (cmt)
CH: cạnh chung
Vậy: \(\Delta ACH=\Delta BCH\left(c-g-c\right)\)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\), HA = HB
Mà \(\widehat{H_1}+\widehat{H_2}=180^o\)
Nên \(\widehat{H_1}=\widehat{H_2}\) = 90o
Do đó: \(CH\perp AB\)
Vì \(CD\perp AB\)và HA = HB nên CD là đường trung trực của AB.
Bài II.3 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 153)
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CD. Gọi I là giao điểm của BE và CD
a) Chứng minh rằng IB = IC, ID = IE
b) Chứng minh rằng BC song song với DE
c) Gọi M là trung điểm của BC. Chứng minh rằng ba điểm A, M, I thẳng hàng
Hướng dẫn giải
a) Vì AB = AC (do \(\Delta ABC\) cân tại A)
BD = CE (gt)
=> AD = AE
Xét hai tam giác ABE và ACD có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
AD = AE (cmt)
Vậy: \(\Delta ABE=\Delta ACD\left(c-g-c\right)\)
Suy ra: BE = CD (hai cạnh tương ứng) (1)
\(\widehat{ABE}=\widehat{ACD}\) (hai góc tương ứng) (2)
\(\Delta ABC\) cân tại A nên \(\widehat{B_1}=\widehat{C_1}\) (3)
Từ (2) và (3) suy ra:
\(\widehat{ABE}-\widehat{B_1}=\widehat{ACD}-\widehat{C_1}\) hay \(\widehat{B_2}=\widehat{C_2}\)
Vậy \(\Delta BIC\) cân tại I, suy ra: IB = IC (4)
Từ (1) và (4) suy ra:
BE - IB = CD - IC hay IE = ID
b) Các tam giác cân ABC và ADE có chung góc ở đỉnh A nên \(\widehat{B_1}=\widehat{ADE}\) (hai góc đồng vị)
Do đó: BC // DE
c) Xét hai tam giác BIM và CIM có:
MB = MC (gt)
\(\widehat{B_2}=\widehat{C_2}\)(cmt)
IB = IC (do \(\Delta BIC\) cân tại I)
Vậy: \(\Delta BIM=\Delta CIM\left(c-g-c\right)\)
Suy ra: \(\widehat{IMB}=\widehat{IMC}\) (hai góc tương ứng)
Mà \(\widehat{IMB}+\widehat{IMC}=180^o\) (kề bù)
Nên \(\widehat{IMB}=\widehat{IMC}\) = 90o (1)
Ta lại có: \(\widehat{IMB}+\widehat{AMB}=180^o\) (kề bù)
Mà \(\widehat{IMB}=90^o\)
\(\Rightarrow\widehat{AMB}=90^o\) (2)
Từ (1) và (2) suy ra: ba điểm A, M, I thẳng hàng (đpcm).
Bài II.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 153)
Cho hình bs.7.
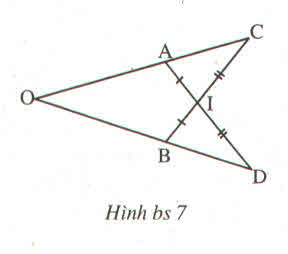
Chứng minh rằng OA = OB ?
Hướng dẫn giải
Xét tam giác IAC và IBD có:
IA = IB ( theo đề bài)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( theo đề bài )
Do đó: tam giác IAC = tam giác IBD (c.g.c)
Suy ra góc ACI = góc BDI ( 2 góc tương ứng) \(\left(1\right)\)
Suy ra góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = \(180^0\)(2 góc kề bù)
góc OBI + góc IBD = \(180^0\)(2 góc kề bù)
mà: góc IAC = góc IBD (*)
Suy ra góc: OAI = góc OBI (5)
Xét tam giác: OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
Do đó: tam giác OAD = tam giác OBC (g.c.g)
Suy ra: OA = OB (2 cạnh tương ứng)
Bài 105 (Sách bài tập - tập 1 - trang 152)
Cho hình 69 trong đó \(AE\perp BC\)
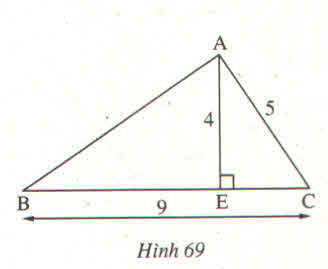
Tính AB biết AE = 4m, AC = 5m, BC = 9m
Hướng dẫn giải
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)
Bài II.1 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 153)
Trên hình bs.6
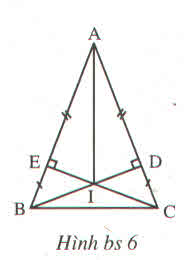
Có bao nhiêu cặp tam giác bằng nhau ?
(A) 2 (B) 3 (C) 4 (D) 5
Hãy chọn phương án đúng ?
Hướng dẫn giải
D
Có thể bạn quan tâm
Có thể bạn quan tâm
