Bài 3: Nhị thức Niu-tơn
NHỊ THỨC NIU-TƠN
1) Công thức nhị thức Niu-tơn
Định lý:
\(\left(a+b\right)^n=C^0_na^n+C^1_na^{n-1}b+...+C^k_na^{n-k}b^k+...+C^{n-1}_nab^{n-1}+C^n_bb^n\) (1)
Định lý này ta thừa nhận (không chứng minh trong chương trình Toán phổ thông).
Công thức nhị thức Niu-tơn ở trên có thể viết gọn lại thành
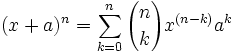
với:
\(\left(\begin{matrix}n\\k\end{matrix}\right)=C^k_n=\frac{n!}{k!\left(n-k\right)!}\)
Chú ý rằng:
- Lũy thừa của x giảm dần cho tới khi đạt đến 0 (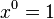
), giá trị bắt đầu là n (n trong 
.)
- Lũy thừa của y tăng lên bắt đầu từ 0 (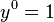
) cho tới khi đạt đến n (n trong .)
- Hàng nhị thức của tam giác Pascal sẽ là các hệ số của nhị thức mở rộng (chú ý rằng đỉnh là hàng 0)
- Với mỗi hàng, tích số (tổng của các hệ số) bằng 
.
- Với mỗi hàng, nhóm tích số bằng 
.
Ví dụ:
\(\left(a+b\right)^2=C^0_2a^2+C^1_2a.b+C^2_2b^2=a^2+2ab+b^2\)
\(\left(a+b\right)^3=C^0_3a^3+C^1_3a^2b+C^2_3ab^2+C^3_3b^3=a^3+3a^2b+3ab^2+b^3\)
2) Tam giác Pa-xcan
Trong nhị thức Niu-tơn (1) ở trên, cho n = 0; 1; 2; ... và xếp các hệ số \(C^k_n\) thành dòng, ta nhận được tam giác sau (còn gọi là tam giác Pa-xcan)
Trong tam giác trên, mỗi phần tử ở dòng dưới bằng tổng của hai phần tử đứng ngay trên đầu nó ở dòng trên, ví dụ dòng ứng với n = 5, số 10 trong dòng này bằng tổng của 2 số 4 và 6 ở dòng n = 4. Ta có cách làm này là do tính chất sau:
\(C_n^k=C_{n-1}^{k-1}+C^k_{n-1}\)
Nhờ tam giác Pa-xcan mà ta có thể triển khai lũy thừa bậc n của tổng hai số một cách dễ dàng mà không cần phải tính \(C^k_n\). Ví dụ:
\(\left(a+b\right)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6\)
Chú ý:
- Định lý nhị thức có thể áp dụng với lũy thừa của bất cứ nhị thức nào. Ví dụ:
- Với một nhị thức có phép trừ, định lý có thể được áp dụng khi chuyển phép trừ thành phép cộng với số đối, ví dụ:
\(\left(a-b\right)^3=\left[a+\left(-b\right)\right]^3=a^3+3a^2\left(-b\right)+3a\left(-b\right)^2+\left(-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
- Trong trường hợp tổng quát trên trường số phức: Nếu r là một số thực và z là một số phức có môđun nhỏ hơn 1 thì:
TÀI LIỆU THAM KHẢO
Nhị thức Newton, các dạng toán thi đại học
Các dạng toán về Tổ hợp và xác suất
Bài tập
Có thể bạn quan tâm
Có thể bạn quan tâm
