Định lý Talet trong tam giác
Lý thuyết
Mục lục
* * * * *
Bài 1 (Sgk tập 2 - trang 58)
Viết tỉ số của các cặp đoạn thẳng có độ dài như sau :
a) AB = 5cm và CD = 15cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
Hướng dẫn giải
Bài 2 (Sgk tập 2 - trang 59)
Cho biết \(\dfrac{AB}{CD}=\dfrac{3}{4}\) và \(CD=12cm\). Tính độ dài của AB ?
Hướng dẫn giải
Ta có: = mà CD= 12cm nên
= => A= = 9
Vậy độ dài AB= 9cm.
Bài 3 (Sgk tập 2 - trang 59)
Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B' ?
Hướng dẫn giải
Độ dài AB gấp 5 lần độ dài CD nên AB= 5CD.
Độ dài A'B' gấp 12 lần độ dài CD nên A'B'= 12CD.
=> Tí số của hai đoạn thẳng AB và A'B' là:
= =
Bài 4 (Sgk tập 2 - trang 59)
Cho biết \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\left(h.6\right)\)
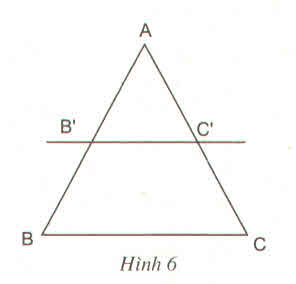
Chứng minh rằng :
a) \(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\)
b) \(\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)
Hướng dẫn : Áp dụng tính chất của tỉ lệ thức
Hướng dẫn giải
a) Ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\Rightarrow\dfrac{AB}{AC}=\dfrac{AB'}{AC'}\)
Áp dụng tc dãy tỉ số bằng nhau ta có;
\(\dfrac{AB}{AC}=\dfrac{AB'}{AC'}=\dfrac{AB-AB'}{AC-AC'}=\dfrac{BB'}{CC'}\)
\(\Rightarrow\dfrac{AB'}{AC'}=\dfrac{BB'}{CC'}\Leftrightarrow\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
b) Ta có:
\(\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\left(cmt\right)\)
\(\Leftrightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Leftrightarrow\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)
Bài 5 (Sgk tập 2 - trang 59)
Tính \(x\) trong các trường hợp sau (h.7)
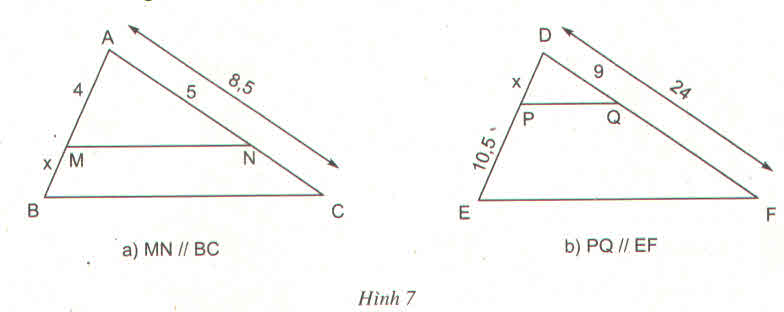
Hướng dẫn giải
a) MN // BC => =
Mà CN = AN= 8.5 - 5= 3.5
nên = => x = = 1,4.
Vậy x = 1,4.
b)
PQ // EF => =
Mà QF = DF - DQ = 24 - 9 = 15
Nên
= => x = = 6,3
Có thể bạn quan tâm
Có thể bạn quan tâm
