§3. Dấu của nhị thức bậc nhất

Lý thuyết

Bài 1 (SGK trang 94)

Xét dấu các biểu thức :

a. \(f\left(x\right)=\left(2x-1\right)\left(x+3\right)\)

b. \(f\left(x\right)=\left(-3x-3\right)\left(x+2\right)\left(x+3\right)\)

c. \(f\left(x\right)=-\dfrac{4}{3x+1}-\dfrac{3}{2-x}\)

d. \(f\left(x\right)=4x^2-1\)

Hướng dẫn giải

a) Ta lập bảng xét dấu

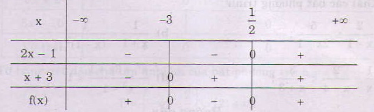
Kết luận: f(x) < 0 nếu - 3 < x <

f(x) = 0 nếu x = - 3 hoặc x =

f(x) > 0 nếu x < - 3 hoặc x > .

b) Làm tương tự câu a).

f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)

f(x) = 0 với x = - 3, - 2, - 1

f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).

c) Ta có: f(x) =

Làm tương tự câu b).

f(x) không xác định nếu x = hoặc x = 2

f(x) < 0 với x ∈ ∪

f(x) > 0 với x ∈ ∪ (2; +∞).

d) f(x) = 4x² – 1 = (2x - 1)(2x + 1).

f(x) = 0 với x =

f(x) < 0 với x ∈

f(x) > 0 với x ∈ ∪

Bài 2 (SGK trang 94)

Giải các bất phương trình :

a. \(\dfrac{2}{x-1}\le\dfrac{5}{2x-1}\)

b. \(\dfrac{1}{x+1}< \dfrac{1}{\left(x-1\right)^2}\)

c. \(\dfrac{1}{x}+\dfrac{2}{x+4}< \dfrac{3}{x+3}\)

d. \(\dfrac{x^2-3x+1}{x^2-1}< 1\)

Hướng dẫn giải

a)

<=> f(x) = .

Xét dấu của f(x) ta được tập nghiệm của bất phương trình:

T = ∪ [3; +∞).

b)

<=> f(x) = = .

f(x) không xác định với x = ± 1.

Xét dấu của f(x) cho tập nghiệm của bất phương trình:

T = (-∞; - 1) ∪ (0; 1) ∪ (1; 3).

c) <=> f(x) =

= .

Tập nghiệm: \(\left(-12;-4\right)\cup\left(-3;0\right)\).

Bài 3 (SGK trang 94)

Giải các bất phương trình :

a. \(\left|5x-4\right|\ge6\)

b. \(\left|-\dfrac{5}{x+2}\right|< \left|\dfrac{10}{x-1}\right|\)

Hướng dẫn giải

a, \(\left|5x-4\right|\ge6\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-4\ge6\\5x-4\le-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-\dfrac{2}{5}\end{matrix}\right.\)

Bài 27 (SBT trang 114)

Xét dấu các biểu thức sau :

\(f\left(x\right)=\left(-2x+3\right)\left(x-2\right)\left(x+4\right)\)

Hướng dẫn giải

\(-2x+3=0\Leftrightarrow x=\dfrac{3}{2}\); \(x-2=0\Leftrightarrow x=2\); \(x+4=0\Leftrightarrow x=-4\).
Ta có:

Vậy \(f\left(x\right)=0\) khi \(x=\left\{-4;\dfrac{3}{2};2\right\}\).
\(f\left(x\right)>0\) khi \(\left(-\infty:-4\right)\cup\left(\dfrac{3}{2};2\right)\).
\(f\left(x\right)< 0\) khi \(\left(-4;\dfrac{3}{2}\right)\cup\left(2;+\infty\right)\).

Bài 28 (SBT trang 114)

Xét dấu các biểu thức sau :

               \(f\left(x\right)=\dfrac{2x+1}{\left(x-1\right)\left(x+2\right)}\)

Hướng dẫn giải

\(2x+1=0\Leftrightarrow x=-\dfrac{1}{2}\);\(x-1=0\Leftrightarrow x=1\); \(x+2=0\Leftrightarrow x=-2\).

Vậy \(f\left(x\right)=0\) khi \(x=\dfrac{1}{2}\);
\(f\left(x\right)>0\) khi \(x\in\left(-2;-\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\).
\(f\left(x\right)< 0\) khi \(x\in\left(-\infty;-2\right)\cup\left(-\dfrac{1}{2};1\right)\).

Bài 29 (SBT trang 114)

Xét dấu các biểu thức sau :

                 \(f\left(x\right)=\dfrac{3}{2x-1}-\dfrac{1}{x+2}\)

Hướng dẫn giải

\(f\left(x\right)=\dfrac{3}{2x-1}-\dfrac{1}{x+2}=\dfrac{3\left(x+2\right)-\left(2x-1\right)}{\left(2x-1\right)\left(x+2\right)}\)
\(=\dfrac{x+7}{\left(2x-1\right)\left(x+2\right)}\).
\(x+7=0\Leftrightarrow x=-7\); \(2x-1=0\Leftrightarrow x=\dfrac{1}{2}\); \(x+2=0\Leftrightarrow x=-2\).

Vậy \(f\left(x\right)=0\) khi \(x=\left\{-7\right\}\).
\(f\left(x\right)>0\) khi \(x\in\left(-7;-2\right)\cup\left(\dfrac{1}{2};+\infty\right)\).
\(f\left(x\right)< 0\) khi \(\left(-\infty;-7\right)\cup\left(-2;\dfrac{1}{2}\right)\).
\(f\left(x\right)\) không xác định tại \(x=\left\{\dfrac{1}{2};-2\right\}\)

Bài 30 (SBT trang 114)

Xét dấu các biểu thức sau :

                 \(f\left(x\right)=\left(4x-1\right)\left(x+2\right)\left(3x-5\right)\left(-2x+7\right)\)

Hướng dẫn giải

Xét:
\(4x-1=0\Leftrightarrow x=\dfrac{1}{4}\); \(x+2=0\Leftrightarrow x=-2\);
\(3x-5=0\Leftrightarrow x=\dfrac{5}{3}\); \(-2x+7=0\Leftrightarrow x=\dfrac{7}{2}\).

Vậy: \(f\left(x\right)=0\) khi \(x=\left\{-2;-\dfrac{1}{4};\dfrac{5}{3};\dfrac{7}{2}\right\}\).
\(f\left(x\right)>0\) khi \(\left(-2;-\dfrac{1}{4}\right)\cup\left(\dfrac{5}{3};\dfrac{7}{2}\right)\).
\(f\left(x\right)< 0\) khi \(\left(-\infty;-2\right)\cup\left(-\dfrac{1}{4};\dfrac{5}{3}\right)\cup\left(\dfrac{7}{2};+\infty\right)\).

Bài 31 (SBT trang 114)

Giải các bất phương trình sau :

                   \(\dfrac{3}{2-x}< 1\) 

Hướng dẫn giải

Ta có : \(\dfrac{3}{2-x}< 1\)

\(\Leftrightarrow3< 2-x\)

\(\Leftrightarrow2-x>3\)

\(\Leftrightarrow-x>3-2\)

\(\Leftrightarrow-x>1\\\Leftrightarrow x< -1 \)

Bài 32 (SBT trang 114)

Giải các bất phương trình sau :

             \(\dfrac{x^2+x-3}{x^2-4}\ge1\)

Hướng dẫn giải

Đkxđ: \(x\ne\pm2\)
\(\dfrac{x^2+x-3}{x^2-4}\ge1\)\(\Leftrightarrow\dfrac{x^2+x-3}{x^2-4}-\dfrac{x^2-4}{x^2-4}\ge0\)
\(\Leftrightarrow\dfrac{x^2+x-3-x^2+4}{x^2-4}\ge0\)\(\Leftrightarrow\dfrac{x+1}{\left(x-2\right)\left(x+2\right)}\ge0\)
Đặt \(f\left(x\right)=\dfrac{x+1}{\left(x-2\right)\left(x+2\right)}\ge0\).
Ta có:

Vậy tập nghiệm của BPT là: ( -2 ; -1] \(\cup\)\(\left(2;+\infty\right)\).

Bài 33 (SBT trang 114)

Giải các bất phương trình sau :

                 \(\dfrac{1}{x-1}+\dfrac{1}{x+2}>\dfrac{1}{x-2}\)

Hướng dẫn giải

\(\Leftrightarrow\dfrac{1}{x-1}>\dfrac{1}{x-2}-\dfrac{1}{x+2}=\dfrac{\left(x+2\right)-\left(x-2\right)}{x^2-4}=\dfrac{4}{x^2-4}\)\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{4}{x^2-4}>0\Leftrightarrow\dfrac{x^2-4-4x+4}{\left(x-2\right)\left(x-1\right)\left(x+2\right)}>0\)

\(\Leftrightarrow A=\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x-1\right)\left(x+2\right)}>0\)

Điều kiện tồn tại A

\(\left\{{}\begin{matrix}x\ne2\\x\ne1\\x\ne-2\end{matrix}\right.\) \(\Rightarrow A=\dfrac{x}{\left(x-1\right)\left(x+2\right)}\)

\(\left\{{}\begin{matrix}x>0\\\left[{}\begin{matrix}x< -2\\x>1\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow x>1\)(1)

\(\left\{{}\begin{matrix}x< 0\\-2< x< 1\end{matrix}\right.\) \(\Rightarrow-2< x< 0\)(2)

từ (1)&(2)kết luận\(\Rightarrow\left[{}\begin{matrix}-2< x< 0\\x>1\end{matrix}\right.\)

Bài 34 (SBT trang 114)

Giải các bất phương trình sau :

              \(\left|x-3\right|>-1\)

Hướng dẫn giải

\(\left|x-3\right|>-1\)

VT >=0 mọi x

VP <0 mọi x

=> BPT đúng với mọi x

Bài 35 (SBT trang 114)

Giải các bất phương trình sau :

           \(\left|5-8x\right|\le11\)

Hướng dẫn giải

bài này đơn giản nhưng mình thấy ấn tượng nhất chỗ này

bước đổi dấu trong trị tuyệt đối này đúng

Bài 36 (SBT trang 114)

Giải các bất phương trình sau :

              \(x+2+\left|-2x+1\right|\le x+1\)

Hướng dẫn giải

\(\Leftrightarrow\left|2x-1\right|\le-1\)

VP >=0 mọi x

VT<0 => vô nghiệm