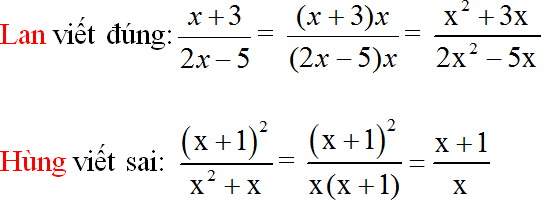Tính chất cơ bản của phân thức
Lý thuyết
Mục lục
* * * * *
Bài 5 (SGK tập 1 - trang 38)
Điền đa thức thích hợp vào mỗi chỗ trống trong các đẳng thức sau :
a) \(\dfrac{x^3+x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{.....}{x-1}\)
b) \(\dfrac{5\left(x+y\right)}{2}=\dfrac{5x^2-5y^2}{.........}\)
Hướng dẫn giải
Bài 4 (SGK tập 1 - trang 38)
Cô giáo yêu cầu mỗi bạn cho một ví dụ về hai phân thức bằng nhau. Dưới đây là những ví dụ mà các bạn Lan, Hùng, Giang, Huy đã cho :
Lan \(\dfrac{x+3}{2x-5}=\dfrac{x^2+3x}{2x^2-5x}\)
Hùng \(\dfrac{\left(x+1\right)^2}{x^2+x}=\dfrac{x+1}{1}\)
Giang \(\dfrac{4-x}{-3x}=\dfrac{x-4}{3x}\)
Huy \(\dfrac{\left(x-9\right)^3}{2\left(9-x\right)}=\dfrac{\left(9-x\right)^2}{2}\)
Em hãy dùng tính chất cơ bản của phân thức và quy tắc đổi dấu để giải thích ai viết đúng, ai viết sai. Nếu có chỗ nào sai, em hãy sửa lại cho đúng ?
Hướng dẫn giải
Bài 6 (SGK tập 1 - trang 38)
Đố :
Hãy dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống :
\(\dfrac{x^5-1}{x^2-1}=\dfrac{........}{x+1}\)
Hướng dẫn giải
tính chất quan trọng phần thức với
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc\Rightarrow c=\dfrac{ad}{b}\)áp vào
\(\dfrac{x^5-1}{x^2-1}=\dfrac{A}{x+1}\Rightarrow A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{x^2-1}\) {x khác +-1}
\(A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left[\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\right]\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\left(x^4+x^3+x^2+x+1\right)\)
Vậy đa thức cần điền là
\(A=\left(x^4+x^3+x^2+x+1\right)\)
Có thể bạn quan tâm
Có thể bạn quan tâm
