Diện tích tam giác
Bài 16 (Sgk tập 1 - trang 121)
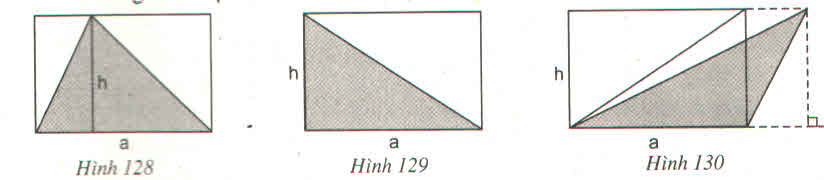
Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128, 129, 130 bằng nửa diện tích hình chữ nhật tương ứng ?
Hướng dẫn giải
Ở mỗi hình 128, 129, 130: hình tam giác và hình chữ nhật đều có cùng đáy a và cùng chiều cao b nên diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.
Bài 17 (Sgk tập 1 - trang 121)
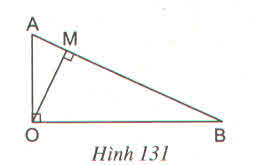
Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức :
AB . OM = AO .OB
Hướng dẫn giải
Ta có cách tính diện tích AOB với đường cao OM và cạnh đáy AB:
S = \(\dfrac{1}{2}\) OM. AB
Ta lại có cacnhs tính diện tích AOB vuông với hai cạnh góc vuông OA, OB là
S = \(\dfrac{1}{2}\) OA.OB
Suy ra AB. OM = OA. OB (2S).
Bài 18 (Sgk tập 1 - trang 121)
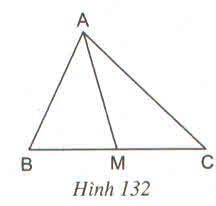
Cho tam giác ABC và đường trung tuyến AM (h.132)
Chứng minh :
\(S_{AMB}=S_{AMC}\)
Hướng dẫn giải
Ta có :
SAMB = \(\dfrac{1}{2}\) BM. AH
SAMC = \(\dfrac{1}{2}\)CM. AH
mà BM = CM (vì AM là đường trung tuyến)
Vậy SAMB = SAMC
Bài 19 (Sgk tập 1 - trang 122)
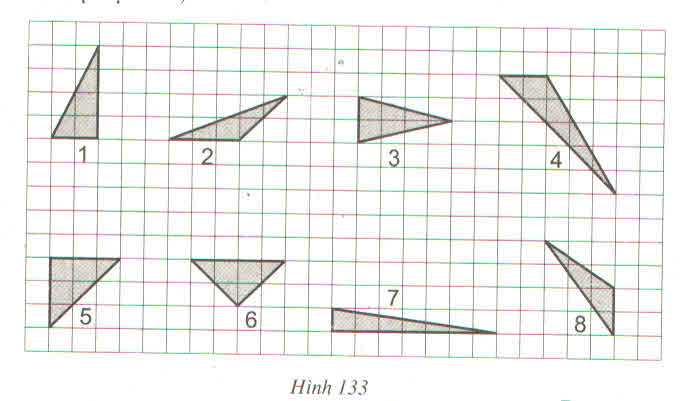
a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)
b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không ?
Hướng dẫn giải
a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.
Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.
Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác(diện tích tam giác số 4 là 5 ô vuông, tam giác số là 4,5 ô vuông, tam giác số 7 là 3,5 ô vuông).
b) Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.
Bài 20 (Sgk tập 1 - trang 122)
Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác ?
Hướng dẫn giải
Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
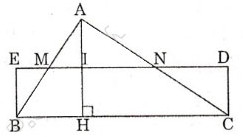
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC=  BC. AH
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.
Bài 21 (Sgk tập 1 - trang 122)
Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE (h.134) ?
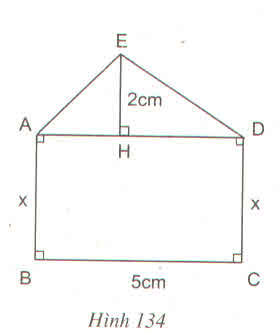
Hướng dẫn giải
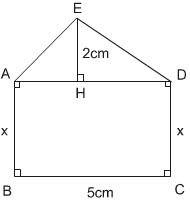
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm
Bài 22 (Sgk tập 1 - trang 122)
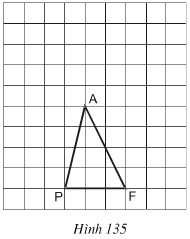
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135)
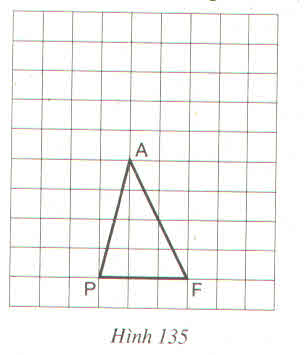
Hãy chỉ ra :
a) Một điểm I sao cho \(S_{PIF}=S_{PAF}\)
b) Một điểm O sao cho \(S_{POF}=2.S_{PAF}\)
c) Một điểm N sao cho \(S_{PNF}=\dfrac{1}{2}S_{PAF}\)
Hướng dẫn giải
Bài 23 (Sgk tập 1 - trang 123)
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho :
\(S_{AMB}+S_{BMC}=S_{MAC}\)
Hướng dẫn giải
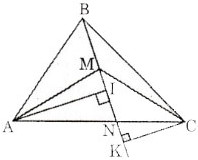
Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho SMAC = SAMB + SBMC
Nhưng SAMB + SBMC + SMAC = SABC
Suy ra SMAC = SABC
∆ MAC = ∆ABC có chung đáy BC nên MK =  BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
>>>>> Bí kíp học tốt các môn lớp 8 2017 bởi các Thầy C
Bài 24 (Sgk tập 1 - trang 123)
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b ?
Hướng dẫn giải
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
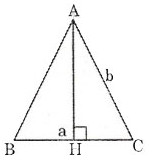
Theo định lý Pitago ta có
h2 = b2 -  =
= 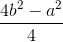
h = 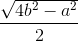
Nên S =  ah =
ah =  a.
a. 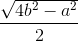 =
=  a.
a. 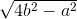 .
.
Bài 25 (Sgk tập 1 - trang 123)
Tính diện tích của một tam giác đều có cạnh bằng a ?
Hướng dẫn giải
Gọi h là chiều cao của tam giác đều cạnh a
Theo định lí Pitago ta có:
Nên
Vậy




