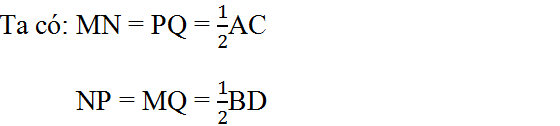Diện tích hình thoi

Lý thuyết

• Bài 33 (Sgk tập 1 - trang 128)
• Bài 32 (Sgk tập 1 - trang 128)
• Bài 36 (Sgk tập 1 - trang 129)
• Bài 34 (Sgk tập 1 - trang 128)
• Bài 35 (Sgk tập 1 - trang 129)

Bài 33 (Sgk tập 1 - trang 128)

Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Hướng dẫn giải

Bài 32 (Sgk tập 1 - trang 128)

a) Hãy vẽ một tứ giác có độ dài hai đường chéo là : 3,6cm, 6cm và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy ? Hãy tính diện tích mỗi tứ giác vừa vẽ

b) Hãy tính diện tích hình vuông có độ dài đường chéo là d

Hướng dẫn giải

a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác ABCD ở hình dưới có

AC = 6cm

BD = 3,6cm

AC $\perp$ BD

Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:

AC = 6cm

BD = 3,6cm

AC $\perp$ BD tại I với I là điểm tùy ý thuộc đoạn AC và BD

Diện tích củ tứ giác vừa vẽ:

S_ABCD = $\frac{1}{2}$ AC. BD = $\frac{1}{2}$ 6. 3,6 = 10,8 (cm²)

b) Diện tích hình vuông có độ dài đường chéo là d

Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:

S = $\frac{1}{2}$ d.d = $\frac{1}{2}$ d²

Bài 36 (Sgk tập 1 - trang 129)

Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn  ? Vì sao ?

Hướng dẫn giải

Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a.

Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là a

Ta có: S_MNPQ = a²

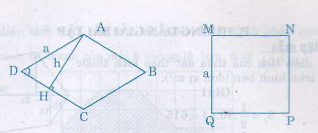
Từ đỉnh góc tù A của hình thoi ABCD vẽ đường cao AH có độ dài h.

Khi đó S_ABCD = ah

Nhưng h ≤ a (đường vuông góc nhỏ hơn đường xiên) nên ah ≤ a²

Vậy S_ABCD ≤ S_MNPQ

Dấu "=" xảy ra khi h = a hay H trùng với D, nghĩa là hình thoi ABCD trở thành hình vuông.

Bài 34 (Sgk tập 1 - trang 128)

Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi ? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Hướng dẫn giải

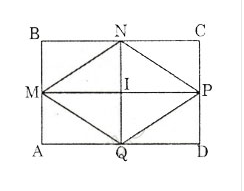
Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm của AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi

Ta có MN = PQ = 1/2BD

NP = MQ = 1/2 AC

Mà AC = BD

⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi (Có 4 cạnh bằng nhau)

* Theo bài 33 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC

Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ

* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP

Bài 35 (Sgk tập 1 - trang 129)

Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là \(60^0\) ?

Hướng dẫn giải

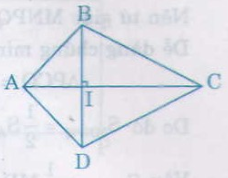
Cho hình thoi ABCD có cạnh AB = 6cm, ∠A = 600

+ ABCD là hình thoi ⇒ ΔBAD cân tại A. Mà ∠A = 600 nên ΔABD là tam giác đều ⇒ BD = AB = 6cm

+ AC ⊥ BD và BI = ID = 3cm

Trong tam giác vuông AIB áp dụng định lý pitago

AI2 = AB2 – IB2 = 36 – 9 = 27 ⇒ AI = √27 (cm)

Suy ra: AC = 2AI = 2√27 (cm)

Vậy SABCD = 1/2AC.BD = 1/2.2√27 .6 = 12√27 (cm2)