Bài 4: Cấp số nhân
Bài 1 (SGK trang 103)
Chứng minh các dãy số \(\left(\dfrac{3}{5}.2^n\right),\left(\dfrac{5}{2^n}\right),\left(\left(-\dfrac{1}{2}\right)^n\right)\) là các cấp số nhân ?
Hướng dẫn giải
a) Với mọi ∀n ε N*, ta có (
. 2n+1) : (
. 2n) = 2.
Suy ra un+1 = un.2, với n ε N*
Vậy dãy số đã chp là một câp số nhân với u1 = , q = 2.
b) Với mọi ∀n ε N*, ta có un+1 = =un.
Vậy dãy số đã cho là một cấp số nhân với u1 = , q =
c) Với mọi ∀n ε N*, ta có un+1 = .
Bài 2 (SGK trang 103)
Cho cấp số nhân \(\left(u_n\right)\) với công bội q.
a) Biết \(u_1=2;u_6=486\). Tìm q ?
b) Biết \(q=\dfrac{2}{3};u_4=\dfrac{8}{21}\). Tìm \(u_1\) ?
c) Biết \(u_1=3;q=-2\). Hỏi 192 là số hạng thứ mấy ?
Hướng dẫn giải
Trong bài này ta áp dụng công thức tinh số hạng tổng quát un = u1.qn-1, biết hai đại lượng, ta sẽ tìm đại lượng còn lại:
a) q = 3.
b) u1 =
c) Theo đề bài ta có un = 192, từ đó ta tìm được n. Đáp số: n =7
Bài 3 (SGK trang 103)
Tìm các số hạng của cấp số nhân \(\left(u_n\right)\) có năm số hạng, biết :
a) \(u_3=3\) và \(u_5=27\)
b) \(u_4-u_2=25\) và \(u_3-u_1=50\)
Hướng dẫn giải
a) Áp dụng công thức tính số hạng tổng quát, ta có:
u3 = 3 = u1.q2 và u5 = 27 = u1.q4.
Vì 27 = (u1q2).q2 = 3.q2 nên q2 = 9 hay q = ±3.
Thay q2 = 9 vào công thức chứa u3, ta có u1 = .
- Nếu q = 3, ta có cấp số nhân: , 1, 3, 9, 27.
- Nếu q = -3, ta có cáp số nhân: , -1, 3, -9, 27.
b) Áp dụng công thức tính số hạng tỏng quát từ giả thiết, ta có:
hay
Từ hệ trên ta được: 50.q = 25 => q = .
Và u1 = .
Ta có cấp số nhân .
Bài 4 (SGK trang 104)
Tìm cấp số nhân có 6 số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62 ?
Hướng dẫn giải
Giả sử có cấp số nhân: u1, u2, u3, u4, u5,u6.
Theo giả thiết ta có:
u1 + u2 + u3 + u4 + u5 = 31. (1)
và u2 + u3 + u4 + u5 + u6 = 62. (2)
Nhân hai vế của (1) với q, ta được: q.u1 + q.u2 + q.u3 +q. u4 +q. u5 = 31.q
hay u2 + u3 + u4 + u5 + u6 = 31q
Suy ra 62 = 31.q hay q = 2.
Ta có S5 = 31 = 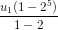 nên suy ra u1 = 1.
nên suy ra u1 = 1.
Vậy ta có cấp số nhân 1, 2, 4, 8, 16, 32.
Bài 5 (SGK trang 104)
Tỉ lệ tăng dân số của tỉnh X là 1,4%. Biết rằng số dân của hiện nay là 1,8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu ?
Hướng dẫn giải
Giả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N
Vậy số dân của tỉnh đó vào năm sau là
N + 1,4%.N = 101,4%.N = .
Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân.
N, ,
, ....
Vậy nếu N = 1,8 triệu người, áp dụng công thức tính số hạng tổng quát của cấp số nhân thì sau 5 năm số dân của tỉnh là ≈ 1,9 (triệu người)
và sau 10 năm sẽ là ≈ 2,1 (triệu người)
Bài 6 (SGK trang 104)
Cho hình vuông \(C_1\) có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \(C_2\) (h44). Từ hình vuông \(C_2\) lại tiếp như trên để được hình vuông \(C_3\),.......Tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \(C_1,C_2,C_3,.....C_n,....\)
Gọi \(a_n\) là độ dài cạnh của hình vuông \(C_n\). Chứng minh dãy dố \(\left(a_n\right)\) là một cấp số nhân ?

Hướng dẫn giải
Xét dãy số (an), ta có a1 = 4.
Giả sử hình vuông cạnh Cn có độ dài cạnh là an. Ta sẽ tính cạnh an+1 của hình vuông Cn+1. Theo hình 9, áp dụng định lí Pi-ta-go, ta có:
an+1 = 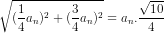 với n ε N*.
với n ε N*.
Vậy dãy số (an) là cấp số nhân với số hạng đầu là a1 = 4 và công bội q =