Bài 1: Giới hạn của dãy số

Lý thuyết

Bài 1.9 (Sách bài tập trang 154)

Dùng kết quả của câu 1.7 để tính giới hạn của các dãy số có số hạng tổng quát như sau :

a) \(u_n=\dfrac{1}{n!}\)

b) \(u_n=\dfrac{\left(-1\right)^n}{2n-1}\)

c) \(u_n=\dfrac{2-n\left(-1\right)^n}{1+2n^2}\)

d) \(u_n=\left(0,99\right)^n\cos n\)

e) \(u_n=5^n-\cos\sqrt{n}\pi\)

Hướng dẫn giải

Bài 1.11 (Sách bài tập trang 154)

Tính tổng các cấp số nhân lùi vô hạn \(1;-\dfrac{1}{2};\dfrac{1}{4};-\dfrac{1}{8};.....;\left(-\dfrac{1}{2}\right)^{n-1}\)

 

Hướng dẫn giải

Bài 1.16 (Sách bài tập trang 156)

Giả sử ABC là tam giác vuông cân tại A với độ dài cạnh góc vuông bằng 1. Ta tạo ra các hình vuông theo các bước sau đây :

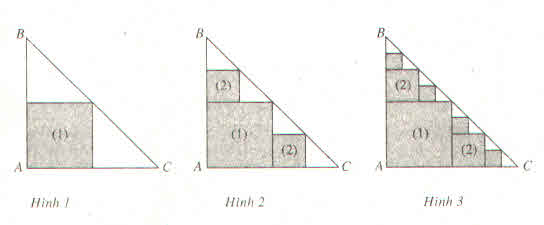
- Bước 1 : Dựng hình vuông mầu xám có một đỉnh là A, ba đỉnh còn lại là các trung điểm của ba cạnh AB, BC và AC (H1). Kí hiệu hình vuông này là (1) 

- Bước 2 : Với 2 tam giác vuông cân mầu trắng còn lại như trong hình 1, ta lại tạo được 2 hình vuông mầu xác khác theo cách trên, kí hiệu là (2) (H2)

- Bước 3 : Với 4 tam giác vuông cân mầu trắng như trong hình 2, ta lại tạo được 4 hình vuông với mầu xám theo cách trên (H3)

- ..........

- Bước n : Ở bước này ta có \(2^{n-1}\) hình vuông với mầu sám được tạo thành theo cách trên, kí hiệu là (n)

a) Gọi \(u_n\) là tổng diện tích của tất cả các hình vuông mới được tạo thành ở bước thứ n.

Chứng minh rằng :

               \(u_n=\dfrac{1}{2^{n+1}}\)

b) Gọi \(S_n\) là tổng diện tích của tất cả các hình vuông mầu xám có được sau n bước. Quan sát hình vẽ để dự đoán giới hạn của \(S_n\) khi \(n\rightarrow+\infty\). Chứng minh dự đoán đó ?

Hướng dẫn giải

Bài 1.5 (Sách bài tập trang 153)

Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi \(n\rightarrow+\infty\)

a) \(a_n=\dfrac{2n-3n^3+1}{n^3+n^2}\)

b) \(b_n=\dfrac{3n^3-5n+1}{n^2+4}\)

c) \(c_n=\dfrac{2n\sqrt{n}}{n^2+2n-1}\)

d) \(d_n=\dfrac{\left(2-3n\right)^3\left(n+1\right)^2}{1-4n^5}\)

e) \(u_n=2^n+\dfrac{1}{n}\)

f) \(v_n=\left(-\dfrac{\sqrt{2}}{\pi}\right)^n+\dfrac{3^n}{4^n}\)

g) \(u_n=\dfrac{3^n-4^n+1}{2.4^n+2^n}\)

h) \(v_n=\dfrac{\sqrt{n^2+n-1}-\sqrt{4n^2-2}}{n+3}\)

Hướng dẫn giải

Bài 1.6 (Sách bài tập trang 154)

Tính các giới hạn sau :

a) \(\lim\limits\left(n^2+2n-5\right)\)

b) \(\lim\limits\left(-n^3-3n^2-2\right)\)

c) \(\lim\limits\left[4^n+\left(-2\right)^n\right]\)

d) \(\lim\limits n\left(\sqrt{n^2-1}-\sqrt{n^2+2}\right)\)

Hướng dẫn giải

Bài 1.3 (Sách bài tập trang 153)

Cho biết dãy số \(\left(u_n\right)\) có giới hạn hữu hạn, còn dãy số \(\left(v_n\right)\) không có giới hạn hữu hạn. Dãy số \(\left(u_n+v_n\right)\) có thể có giới hạn không ?

Hướng dẫn giải

Bài 1.12 (Sách bài tập trang 154)

Tính tổng \(S=1+0,9+\left(0,9\right)^2+\left(0,9\right)^3+....+\left(0,9\right)^{n-1}+...\)

Hướng dẫn giải

S = 1 + 0,9 + 0,9^2 + ...+ 0,9^n + ...
S là tổng của csn có u1 = 1, q = 0,9 (có |q| < 1)
S = u1 / (1 - q) = 1 / (1 - 0,9) = 10.

Bài 1.7 (Sách bài tập trang 154)

Cho hai dãy số \(\left(u_n\right)\) và \(\left(v_n\right)\). Chứng minh rằng nếu \(\lim\limits v_n=0\) và \(\left|u_n\right|\le v_n\) với mọi n thì \(\lim\limits u_n=0\) ?

Hướng dẫn giải

Bài 1.14 (Sách bài tập trang 154)

Cho dãy số \(\left(b_n\right)\) có số hạng tổng quát là \(b_n=\sin\alpha+\sin^2\alpha+....+\sin^n\alpha\) với \(\alpha\ne\dfrac{\pi}{2}+k\pi\). Tìm giới hạn của \(\left(b_n\right)\)

 

Hướng dẫn giải

Bài 1.8 (Sách bài tập trang 154)

Biết \(\left|u_n-2\right|\le\dfrac{1}{3^n}\). Có kết luận gì về giới hạn của dãy số \(\left(u_n\right)\) ?

Hướng dẫn giải

Bài 1.2 (Sách bài tập trang 153)

Vì sao dãy số \(\left(u_n\right)\) với \(u_n=\left(-1\right)^n\) không thể có giới hạn là 0 khi \(n\rightarrow+\infty\) ?

Hướng dẫn giải

Bài 1.15 (Sách bài tập trang 155)

Cho số thập phân vô hạn tuần hoàn \(a=34,121212....\) (chu kì là 12). Hãy viết a dưới dạng một phân số ?

Hướng dẫn giải

\(a=34,\left(12\right)\)

\(=34\dfrac{12}{99}=34\dfrac{4}{33}=\dfrac{1126}{33}\)

Bài 1.10 (Sách bài tập trang 154)

Cho dãy số (\(u_n\)) xác định bởi công thức truy hồi :

\(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{u_n+1}{2};n\ge1\end{matrix}\right.\)

Chứng minh rằng \(\left(u_n\right)\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\)

Tìm giới hạn đó ?

Hướng dẫn giải

Bài 1.13 (Sách bài tập trang 154)

Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội \(q=\dfrac{2}{3}\)

Hướng dẫn giải

Bài 1.4 (Sách bài tập trang 153)

a) Cho hai dãy số \(\left(u_n\right)\) và \(\left(v_n\right)\). Biết \(\lim\limits u_n=-\infty\) và \(v_n\le u_n\) với mọi \(n\). Có kết luận gì về giới hạn của dãy \(\left(v_n\right)\) khi \(n\rightarrow+\infty\) ?

b) Tìm \(\lim\limits v_n\) với \(v_n=-n!\)

Hướng dẫn giải

Bài 1.1 (Sách bài tập trang 153)

Biết rằng dãy số \(\left(u_n\right)\) có giới hạn là 0. Giải thích vì sao dãy số \(\left(v_n\right)\) với \(v_n=\left|u_n\right|\) cũng có giới hạn là 0. Chiều ngược lại có đúng không ?

Hướng dẫn giải