Bài 2: Giới hạn của hàm số
Lý thuyết
Mục lục
* * * * *
Bài 2.11 (Sách bài tập trang 164)
Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;+\infty\right)\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow+\infty}=-\infty\) thì luôn tồn tại ít nhất một số c thuộc \(\left(a;+\infty\right)\) sao cho \(f\left(c\right)< 0\)
Hướng dẫn giải
Bài 2.7 (Sách bài tập trang 164)
Tính giới hạn của các hàm số sau khi \(x\rightarrow+\infty\) và khi \(x\rightarrow-\infty\)
a) \(f\left(x\right)=\dfrac{\sqrt{x^2-3x}}{x+2}\)
b) \(f\left(x\right)=x+\sqrt{x^2-x+1}\)
c) \(f\left(x\right)=\sqrt{x^2-x}-\sqrt{x^2+1}\)
Hướng dẫn giải
Bài 2.3 (Sách bài tập trang 163)
a) Chứng minh rằng hàm số \(y=\sin x\) không có giới hạn khi \(x\rightarrow+\infty\)
b) Giải thích bằng đồ thị kết luận ở câu a)
Hướng dẫn giải
Bài 2.8 (Sách bài tập trang 164)
Cho hàm số :
\(f\left(x\right)=\dfrac{2x^2-15x+12}{x^2-5x+4}\) có đồ thị như hình 4
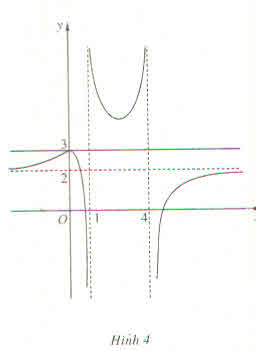
a) Dựa vào đồ thị, dự đoán giới hạn của hàm số \(f\left(x\right)\) khi \(x\rightarrow1^+;x\rightarrow1^-;x\rightarrow4^+;x\rightarrow4^-;x\rightarrow+\infty;x\rightarrow-\infty\)
b) Chứng minh dự đoán trên ?
Hướng dẫn giải
Bài 2.6 (Sách bài tập trang 164)
Tính các giới hạn sau :
a) \(\lim\limits_{x\rightarrow-3}\dfrac{x+3}{x^2+2x-3}\)
b) \(\lim\limits_{x\rightarrow0}\dfrac{\left(1+x\right)^3-1}{x}\)
c) \(\lim\limits_{x\rightarrow+\infty}\dfrac{x-1}{x^2-1}\)
d) \(\lim\limits_{x\rightarrow5}\dfrac{x-5}{\sqrt{x}-\sqrt{5}}\)
e) \(\lim\limits_{x\rightarrow+\infty}\dfrac{x-5}{\sqrt{x}+\sqrt{5}}\)
f) \(\lim\limits_{x\rightarrow-2}\dfrac{\sqrt{x^2+5}-3}{x+2}\)
g) \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{x}-1}{\sqrt{x+3}-2}\)
h) \(\lim\limits_{x\rightarrow+\infty}\dfrac{1-2x+3x^3}{x^3-9}\)
i) \(\lim\limits_{x\rightarrow0}\dfrac{1}{x^2}\left(\dfrac{1}{x^2+1}-1\right)\)
j) \(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(x^2-1\right)\left(1-2x\right)^5}{x^7+x+3}\)
Hướng dẫn giải
Bài 2.5 (Sách bài tập trang 163)
Tìm giới hạn của các hàm số sau :
a) \(f\left(x\right)=\dfrac{x^2-2x-3}{x-1}\) khi \(x\rightarrow3\)
b) \(h\left(x\right)=\dfrac{2x^3+15}{\left(x-2\right)^2}\) khi \(x\rightarrow-2\)
c) \(k\left(x\right)=\sqrt{4x^2-x+1}\) khi \(x\rightarrow-\infty\)
d) \(f\left(x\right)=x^3+x^2+1\) khi \(x\rightarrow-\infty\)
e) \(h\left(x\right)=\dfrac{x-15}{x+2}\) khi \(x\rightarrow-2^+\) và khi \(x\rightarrow-2^-\)
Hướng dẫn giải
Bài 2.10 (Sách bài tập trang 164)
Cho khoảng \(K,x_0\in K\) và hàm số \(y=f\left(x\right)\) xác định trên \(K\)\ \(\left\{x_0\right\}\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\) thì luôn tồn tại ít nhất một số c thuộc \(K\)\ \(\left\{x_0\right\}\) sao cho \(f\left(c\right)>0\)
Hướng dẫn giải
Bài 2.2 (Sách bài tập trang 163)
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}x^2,\left(x\ge0\right)\\x^2-1,\left(x< 0\right)\end{matrix}\right.\)
a) Vẽ đồ thị của hàm số \(f\left(x\right)\). Từ đó dự đoán về giới hạn của \(f\left(x\right)\) khi \(x\rightarrow0\)
b) Dùng định nghĩa chứng minh dự đoán trên
Hướng dẫn giải
Bài 2.4 (Sách bài tập trang 163)
Cho hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cùng xác định trên khoảng \(\left(-\infty;a\right)\). Dùng định nghĩa chứng minh rằng nếu \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=L\) và \(\lim\limits_{x\rightarrow-\infty}g\left(x\right)=M\) thì \(\lim\limits_{x\rightarrow-\infty}f\left(x\right).g\left(x\right)=L.M\)
Hướng dẫn giải
Bài 2.1 (Sách bài tập trang 163)
Dùng định nghĩa tìm các giới hạn :
a) \(\lim\limits_{x\rightarrow5}\dfrac{x+3}{3-x}\)\(\)
b) \(\lim\limits_{x\rightarrow+\infty}\dfrac{x^3+1}{x^2+1}\)
Hướng dẫn giải
Bài 2.9 (Sách bài tập trang 164)
Cho hàm số :
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{1}{x-1}-\dfrac{3}{x^3-1},\left(x>1\right)\\mx+2,\left(x\le1\right)\end{matrix}\right.\)
Với giá trị nào của tham số m thì hàm số \(f\left(x\right)\) có giới hạn \(x\rightarrow1\). Tìm giới hạn này ?
Hướng dẫn giải
Có thể bạn quan tâm
Có thể bạn quan tâm
