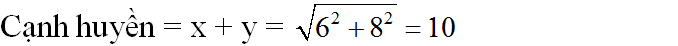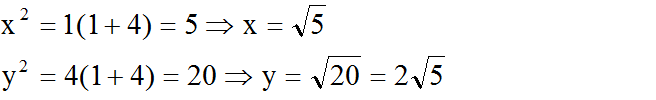Một số hệ thức về cạnh và góc trong tam giác vuông

Lý thuyết

Bài 1 (Sgk tập 1 - trang 68)

Hãy tính x và y trong mỗi hình sau :

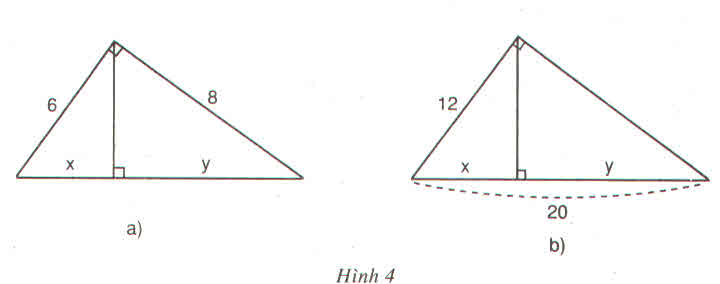
Hướng dẫn giải

Bài 2 (Sgk tập 1 - trang 68)

Hãy tính x và y trong mỗi hình sau :

Hướng dẫn giải

Bài 3 (Sgk tập 1 - trang 69)

Hãy tính x và y trong mỗi hình sau :

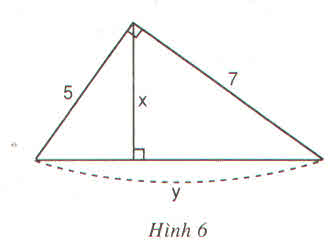
Hướng dẫn giải

Tính cạnh huyền được .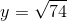

Dùng hệ thức .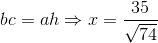

Bài 4 (Sgk tập 1 - trang 69)

Hãy tính x và y trong mỗi hình sau :

 

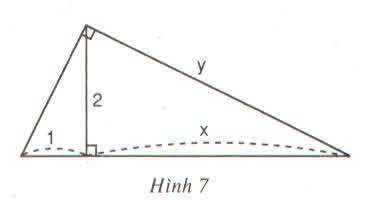
Hướng dẫn giải

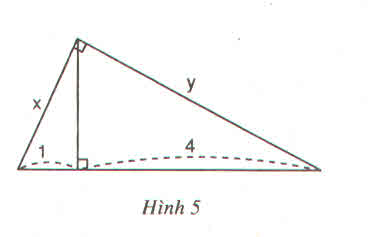
Đặt tên các đỉnh của tam giác như hình bên

Áp dụng hện thức 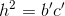ta có:

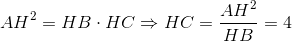
Do đó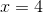

Áp dụng hệ thức 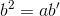ta có

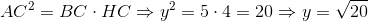
Nhận xét: Ta có thể tính y theo định lý Pi-ta-go:

.

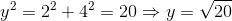Luyện tập - Bài 5 (Sgk tập 1 - trang 69)

Trong tam giác vuông  với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền ?

Hướng dẫn giải

Tính cạnh huyền được BC = 5

ĐS. BH = 1,8; CH = 3,2; AH=2,4.

Luyện tập - Bài 6 (Sgk tập 1 - trang 69)

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này ?

Hướng dẫn giải

ĐS: Hai cạnh góc vuông là: \(AB=\sqrt{3};AC=\sqrt{6}\)

Luyện tập - Bài 7 (Sgk tập 1 - trang 69)

Người ta đưa ra hai cách vẽ đoạn trung bình nhân \(x\) của hai đoạn thẳng a, b (tức là \(x^2=ab\)) như trong hai hình sau :

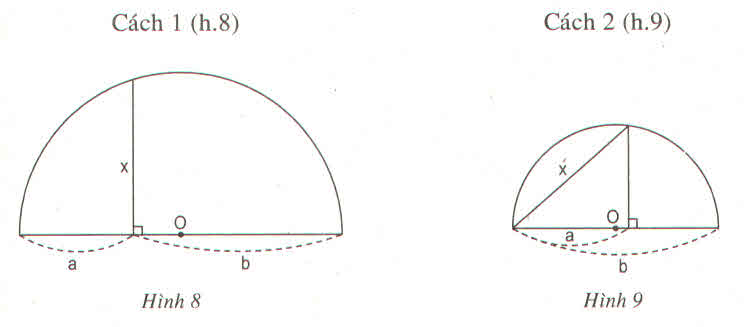
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng

Gợi ý : Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông 

Hướng dẫn giải

Cách 1: Đặt tên các đoạn thẳng như hình bên.

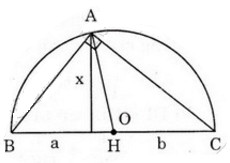
Ta có:

.

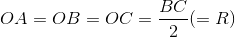Suy ra 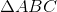vuông tại A.

Áp dụng hệ thức 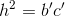ta có: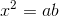

Cách 2:

Cũng chứng minh 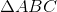vuông như cách 1.

Áp dụng hệ thức 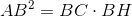ta được .

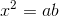Luyện tập - Bài 8 (Sgk tập 1 - trang 70)

Tìm x và y trong mỗi hình sau :

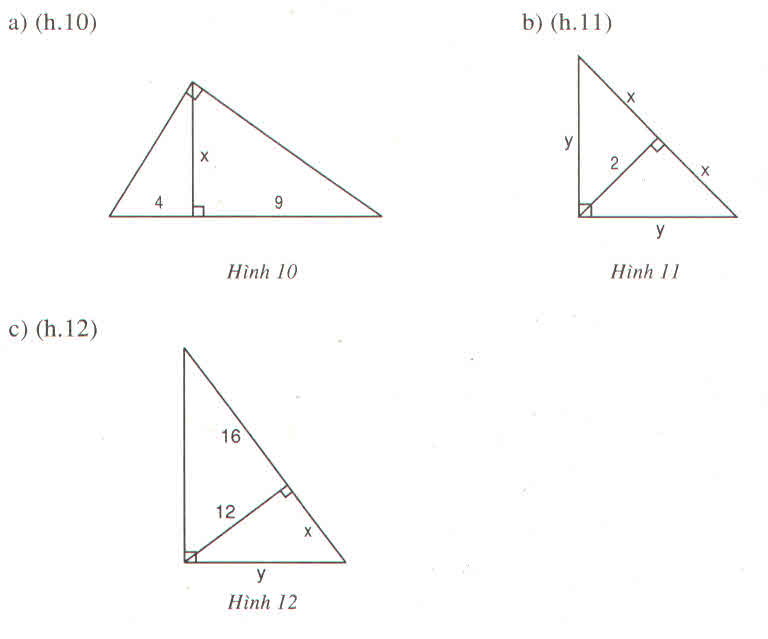
Hướng dẫn giải

a) Ta có: x² = 4.9 = 36 => x = 6
b) Ta có: * 2² = x.x => x² = 4 => x = 2
* y² = x(x + x) = 2.4 = 8 => y = 2√2
c) Ta có: 12² = x.16 => x = 144/16 = 9
Vậy x = 9
y² = x(x + 16) = 6(9 + 16) = 9.25 = 225 => y = 15

Luyện tập - Bài 9 (Sgk tập 1 - trang 70)

Cho hình vuông ABCD. Gọi I là một điểm nẳm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng :

a) Tam giác DIL là một tam giác cân

b) Tổng \(\dfrac{1}{DI^2}+\dfrac{1}{DK^2}\) không đổi khi I thay đổi trên cạnh AB

Hướng dẫn giải

Lời giải: