Số nguyên tố. Hợp số. Bảng số nguyên tố

Lý thuyết

Bài 115 (Sách giáo khoa trang 47)

Các số sau là số nguyên tố hay hợp tố :

         312; 213; 435; 417; 3311; 67

Hướng dẫn giải

Vậy 312 là một hợp số - Vì 3 + 1 + 2 = 6 chia hết cho 3 nên 312 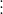3; nghĩa là 312 có ước là 3, khác 1 và 312. .

Tương tự 213 cũng là một hợp số. 435 là một hợp số vì 43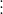5 5.

Vì 3311 = 11 . 301 nên 3311 có ước là 11 và 301. Vậy 3311 là một hợp số.

67 là một số nguyên tố vì nó chỉ có hai ước là 1 và 67.

417 là hợp số vì 417 > 1, có ít nhất 3 ước là 1 ; 3 ; 417

Bài 116 (Sách giáo khoa trang 47)

Gọi P là tập hợp các số nguyên tố. Điền kí hiệu \(\in\), \(\notin\) hoặc \(\subset\) vào ô vuông cho đúng :

a) \(83.......P\)

b) \(91.......P\)

c) \(15.........N\)

d) \(P.......N\)

Hướng dẫn giải

83 ∈ P, 91 P, 15 ∈ N, P ⊂ N.

Bài 117 (Sách giáo khoa trang 47)

Dùng bảng số nguyên tố ở cuối sách, tìm các số nguyên tố trong các số sau :

                    \(117;131;313;647\)

Hướng dẫn giải

Các số nguyên tố là: 131; 313; 647

Bài 118 (Sách giáo khoa trang 47)

Tổng (hiệu) sau là số nguyên tố hay hợp số ?

a) \(3.4.5+6.7\)

b) \(7.9.11.13-2.3.4.7\)

c) \(3.5.7+11.13.17\)

d) \(16354+67541\)

Hướng dẫn giải

a) HD: Xét xem hai số hạng có chia hết cho cùng một số không.

ĐS: 3 . 4 . 5 + 6 . 7 là một hợp số vì 3 . 4 . 5 và 6 . 7 đều chia hết cho 6.

b) 7 . 9 . 11 . 13 - 2 . 3 . 4 . 7 là một hợp số.

c) 3 . 5 . 7 + 11 . 13 . 17 là một hợp số vì tổng là một số chẵn, chia hết cho 2.

d) 16 354 + 67 541 là một hợp số vì tổng là một số tận cùng bởi chữ số 5 nên chia hết cho 5.

Bài 119 (Sách giáo khoa trang 47)

Thay chữ số vào \(\circledast\) để được hợp số : \(\overline{1\circledast};\overline{3\circledast}\) ?

Hướng dẫn giải

Bài giải:

Cách 1: Xét xem mỗi số từ 10 đến 19 (từ 30 đến 39) xem số nào có ước khác 1 và chính nó.

Cách 2: Dùng bảng số nguyên tố ở cuối sách giáo khoa đề loại bỏ các số nguyên tố trong khoảng từ 10 đến 19 (từ 30 đến 39).

ĐS:1*: 10; 12; 14; 15; 16; 18;

3*:30; 32; 33; 34; 35; 36; 38; 39.

Luyện tập - Bài 120 (Sách giáo khoa trang 47)

Thay chữ số vào dấu \(\circledast\) để được số nguyên tố : \(\overline{5\circledast};\overline{9\circledast}\) ?

Hướng dẫn giải

ĐS: 53, 59, 97

Luyện tập - Bài 121 (Sách giáo khoa trang 47)

a) Tìm số tự nhiên k để 3.k là số nguyên tố

b) Tìm số tự nhiên k để 7.k là số nguyên tố

Hướng dẫn giải

a) \(k=1\) vì nếu \(k>1\) thì \(3k⋮3\) \(\rightarrow\)không phải là số nguyên tố

b) ​\(k=1\) vì nếu \(k>1\) thì \(7k⋮7\) \(\rightarrow\) không phải là số nguyên tố

Luyện tập - Bài 122 (Sách giáo khoa trang 47)

Điều dấu "X" vào ô thích hợp :

 

Hướng dẫn giải

a) Đúng. Đó là số 2 và số 3.

b) Đúng. Đó là ba số 3; 5 và 7.

c) Sai. Vì có số 2 là số chẵn đồng thời là số nguyên tố.

d) Sai. Chẳng hạn các số 21, 33, 55, 77, 169 đều không phải là số nguyên tố.

Luyện tập - Bài 123 (Sách giáo khoa trang 48)

Điền vào bảng sau mọi số nguyên tố p mà bình phương của nó không vượt quá a, tức là \(p^2\le a\) 

a	29	67	49	127	173	253
p	2, 3, 5

 

Hướng dẫn giải

a	29	67	49	127	173	253
p	2, 3, 5	2, 3, 5, 7	2, 3, 5, 7	2, 3, 5, 7, 11	2, 3, 5, 7, 11, 13	2, 3, 5, 7, 11, 13

Luyện tập - Bài 124 (Sách giáo khoa trang 48)

Máy bay có động cơ ra đời năm \(\overline{abcd}\), trong đó :

a là số có đúng 1 ước

b là hợp số lẻ nhỏ nhất

c không phải là số nguyên tố, không phải là hợp số và \(c\ne1\)

d là số nguyên tố lẻ nhỏ nhất

Hướng dẫn giải

Vì a là số có đúng 1 ước nên a=1

b là hợp số lẻ nhỏ nhất nên b=1

c không phải là số nguyên tố, không phải là hợp số và \(c\ne1\) nên c=0

d là số nguyên tố lẻ nhỏ nhất nên d=3

Vậy máy bay có động cơ ra đời năm 1103.