Bài 2: Cực trị hàm số
Bài 3 (SGK trang 18)
Chứng minh rằng hàm số \(y=\sqrt{|x|}\) không có đạo hàm tại \(x=0
\) nhưng vẫn đạt cực tiểu tại điểm đó
Hướng dẫn giải
Đặt . Giả sử x > 0, ta có :
Do đó hàm số không có đạo hàm tại x = 0 . Tuy nhiên hàm số đạt cực tiểu tại x = 0 vì .
Bài 4 (SGK trang 18)
Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số \(y=x^3-mx^2-2x+1\)
luôn luôn có một điểm cực đại và một điểm cực tiểu
Hướng dẫn giải
y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.
Bài 2 (SGK trang 18)
Áp dụng quy tắc II, hãy tìm các điểm cực trị của hàm số sau:
a) \(y=x^4-2x^2+1\)
b) \(y=\sin 2x -x\)
c) \(y=\sin x +\cos x\)
d) \(y = x^5 – x^3 – 2x + 1\)
Hướng dẫn giải
a) y' = 4x3 – 4x = 4x(x2 - 1) ; y' = 0 ⇔ 4x(x2 - 1) = 0 ⇔ x = 0, x = 1.
y'' = 12x2 - 4 .
y''(0) = -4 < 0 nên hàm số đạt cực đại tại x = 0, ycđ = y(0) = 1.
y''(1) = 8 > 0 nên hàm số đạt cực tiểu tại x =
1, yct = y(
1) = 0.
b) y' = 2cos2x - 1 ;
y'' = -4sin2x .
nên hàm số đạt cực đại tại các điểm x =
+ kπ, ycđ = sin(
+ k2π) -
- kπ =
- kπ , k ∈ Z.
nên hàm số đạt cực tiểu tại các điểm x =
+ kπ, yct = sin(
+ k2π) +
- kπ =
- kπ , k ∈ Z.
c) y = sinx + cosx = ; y' =
;
![]()
Do đó hàm số đạt cực đại tại các điểm , đạt cực tiểu tại các điểm
d) y' = 5x4 - 3x2 - 2 = (x2 - 1)(5x2 + 2) ; y' = 0 ⇔ x2 - 1 = 0 ⇔ x = ±1.
y'' = 20x3 - 6x.
y''(1) = 14 > 0 nên hàm số đạt cực tiểu tại x = 1, yct = y(1) = -1.
y''(-1) = -14 < 0 hàm số đạt cực đại tại x = -1, ycđ = y(-1) = 3.
Bài 5 (SGK trang 18)
Tìm \(a\) và \(b\) để các cực trị của hàm số
\(y=\dfrac{5}{3}a^2x^3+2ax^2-9x+b\)
đều là những số dương và \(x_0 =-\dfrac{5}{9}\) là điểm cực đại.
Hướng dẫn giải
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
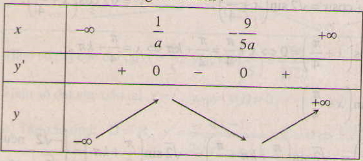
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
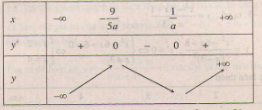
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
Bài 1 (SGK trang 18)
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :
a) \(y = 2x^3 + 3x^2 – 36x – 10\)
b) \(y = x^4+ 2x^2 – 3 ;\)
c) \(y=x+\dfrac{1}{x}\)
d) \(y=x^3(1-x)^2\)
e) \(y=\sqrt{x^2-x+1}\)
Hướng dẫn giải
a) y′=6x2+6x−36=6(x2+x−6)y′=6x2+6x−36=6(x2+x−6)
y’= 0 ⇔ x2+ x – 6= 0 ⇔ x=2; x=-3
Bảng biến thiên :
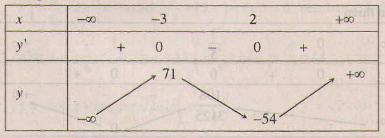
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 , y(ct) = y(2) = -54
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
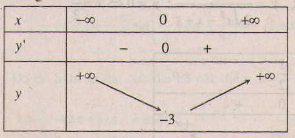
Hàm số đạt cực tiểu tại x = 0 , y(ct) = y(0) = -3
c) Tập xác định : D = R\{0}

Bảng biến thiên :
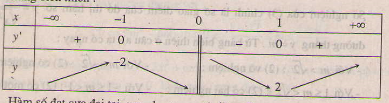
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x = , x = 1.
, x = 1.
Bảng biến thiên :
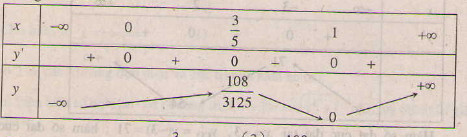
Hàm số đạt cực đại tại x =  , ycđ =
, ycđ =  =
=  ;
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R. 
Hàm số đạt cực tiểu tại 
Bài 6 (SGK trang 18)
Xác định giá trị của tham số m để hàm số \(y=\dfrac{x^2+mx+1}{x+m}\) đạt cực đại tại \(x=2
\)
Hướng dẫn giải
Tập xác định :
Nếu hàm số đạt cực đại tại x = 2 thì y'(2) = 0 ⇔ m2 + 4m + 3 = 0 ⇔ m=-1 hoặc m=-3
- Với m = -1, ta có :
x=0 hoặc x=2.
Ta có bảng biến thiên :
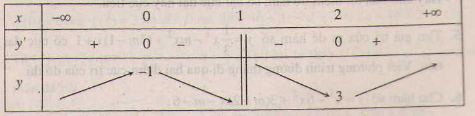
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
- Với m = -3, ta có:
x=2 hoặc x=4
Ta có bản biến thiên :
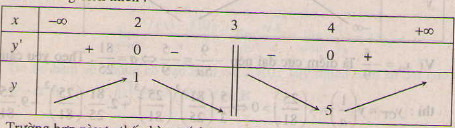
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.




