Đồ thị hàm số y = ax^2 (a khác 0)

Lý thuyết

Bài 11 (Sách bài tập - tập 2 - trang 49)

Cho hàm số :

                        \(y=ax^2\)

a) Xác định hệ số a biết rằng đồ thị của nó cắt đường thẳng \(y=-ax+3\) tại điểm A có hoành độ bằng 1

b) Vẽ đồ thị của hàm số \(y=-2x+3\) và của hàm số \(y=ax^2\) với giá trị của a) vừa tìm được trong câu a trên cùng một mặt phẳng tọa độ

c) Nhờ đồ thị xác định tọa độ của giao điểm thứ hai của hai đồ thị vừa vẽ trong câu b)

Hướng dẫn giải

Bài 8 (Sách bài tập - tập 2 - trang 48)

Cho hàm số \(y=ax^2\). Xác định hệ số a trong các trường hợp sau :

a) Đồ thị của nó đi qua điểm \(A\left(3;12\right)\)

b) Đồ thị của nó đi qua điểm \(B\left(-2;3\right)\)

Hướng dẫn giải

Bài 2.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 51)

Cho hàm số : \(y=0,5x^2\)

a) Tìm các giá trị của \(x\) để \(y<2\)

b) Tìm các giá trị của \(x\) để \(y>2\)

c) Tìm các giá trị của \(y\) khi \(-2< x< 2\)

d) Tìm các giá trị của \(y\) khi \(x\le0\)

e) Tìm các giá trị của \(y\) khi \(x\le2\)

Hướng dẫn giải

Bài 9 (Sách bài tập - tập 2 - trang 48)

Cho hàm số \(y=0,2x^2\)

a) Biết rằng điểm \(A\left(-2;b\right)\) thuộc đồ thị, hãy tính b. Điểm \(A'\left(2;b\right)\) có thuộc đồ thị của hàm số không ? Vì sao ?

b) Biết rằng điểm \(C\left(c;6\right)\) thuộc đồ thị, hãy tính c. Điểm \(D\left(c;-6\right)\) có thuộc đồ thị không ? Vì sao ?

Hướng dẫn giải

Bài 12 (Sách bài tập - tập 2 - trang 49)

Cho hàm số :

                           \(y=\dfrac{3}{4}x^2\)

a) Vẽ đồ thị của hàm số

b) Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A

c) Tìm trên đồ thị các điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách :

- Ước lượng trên đồ thị 

- Tính theo công thức \(y=\dfrac{3}{4}x^2\)

Hướng dẫn giải

Bài 7 (Sách bài tập - tập 2 - trang 48)

Cho hàm số \(y=0,1x^2\)

a) Vẽ đồ thị của hàm số

b) Các điểm sau có thuộc đồ thị hay không : \(A\left(3;0,9\right),B\left(-5;2,5\right),C\left(-10;1\right)\)

 

Hướng dẫn giải

Bài 2.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 51)

a) Xác định hàm số \(y=ax^2\) và vẽ đồ thị của nó, biết rằng đồ thị của nó đi qua điểm \(A\left(-1;2\right)\)

b) Xác định đường thẳng \(y=a'x+b'\) biết rằng đường thẳng này cắt đồ thị của hàm số vừa tìm được trong câu a) tại điểm A và điểm B có tung độ là 8

Hướng dẫn giải

Lời giải

a) A(-1;2)

=> y(-1) =2 <=> a.(-1)^2 =2 => a=2

hàm số được xác định y=2x^2

b) xác đinh tọa độ điểm B

2x^2 =8 => x =+-2

=>có 2 điểm B thỏa mãn

B(2,8) và B'(-2;8)

(d): y=a'x+b'

(d) đi qua A => 2=-a'+b' => b' =2+a'

hay d: y=a'(x+1)+2

(d) đi qua B(2,8) => 8=a'(2+1) +2 => a'=2

(d) đi qu B(-2,8) =>8=a'(-2+1) +2 => a' =-6

vậy

có hai đường thẳng thỏa mãn đầu bài là

d1: y=2x+4

d2:y=-6x-4

đồ thị

Bài 13 (Sách bài tập - tập 2 - trang 49)

Cho hàm số :

                          \(y=f\left(x\right)=-1,5x^2\)

a) Vẽ đồ thị của hàm số 

b) Không làm tính, dùng đồ thị để so sánh \(f\left(-1,5\right)\) và \(f\left(-0,5\right),f\left(0,75\right)\) và \(f\left(1,5\right)\)

c) Dùng đồ thị, tìm những giá trị thích hợp điền vào chỗ trống 

- Khi \(1\le x\le2\) thì \(.........\le y\le.........\)

- Khi \(-2\le x\le0\) thì \(.........\le y\le.........\)

- Khi \(-2\le x\le1\) thì \(.........\le y\le.........\)

Hướng dẫn giải

Bài 2.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 51)

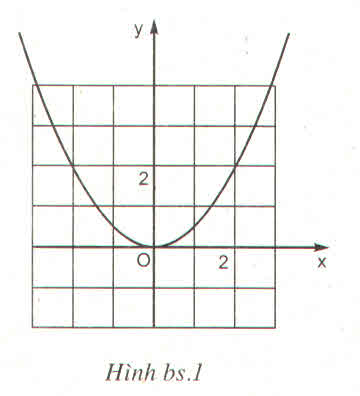
Parabol \(y=ax^2\) trong hình vẽ có hệ số a là bao nhiêu ?

(A) \(1\)                       (B) \(-1\)                           (C) \(2\)                            (D) \(\dfrac{1}{2}\)

Hướng dẫn giải

chọn câu (C) nha bạn

Bài 10 (Sách bài tập - tập 2 - trang 49)

Cho hai hàm số \(y=0,2x^2\) và \(y=x\)

a) Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ ?

b) Tìm tọa độ của những giao điểm của hai đồ thị ?

Hướng dẫn giải

Bài 14 (Sách bài tập - tập 2 - trang 50)

Chơi mà học :

Vẽ parabol 

Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho \(OK=\dfrac{1}{2}\) (đơn vị độ dài nói trến). Lấy điểm \(H\left(0;-\dfrac{1}{2}\right)\). Qua H kẻ đường thẳng Ht // Ox

- Đặt tờ giấy kính lên tờ giấy đã vẽ năm đường tròn sao cho đường tròn (1) đi qua K và tiếp xúc với Ht và tâm I nằm bên phải Oy. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm A

- Di chuyển tờ giấy kính sang trái sao cho đường tròn (2) đi qua K và tiếp xúc với Ht. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm B (xem hình 4)

- Tiếp tục làm như thế đối với các đường tròn còn lại ta lần lượt được các điểm C, D, E trên tờ giấy kính

- Lấy các điểm A', B', C', D' , E' lần lượt đối xứng với các điểm A, B, C, D, E qua Oy

- Nối các điểm E', D', C', B', A', O, A, B, C, D, E bới một đường cong ta được một parabol

 

Hướng dẫn giải