Diện tích tam giác
Bài 3.3 - Bài tập bổ sung (Sách bài tập - trang 161)
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)
Hướng dẫn giải


Bài 30 (Sách bài tập - trang 160)
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C ?
Hướng dẫn giải
Câu hỏi của Hatsune Miku - Toán lớp 8 - Học toán với OnlineMath
Bài 29 (Sách bài tập - trang 160)
Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau :
a) \(10cm^2\)
b) \(15cm^2\)
c) \(20cm^2\)
Hướng dẫn giải
Bài 31 (Sách bài tập - trang 160)
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành 3 đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm
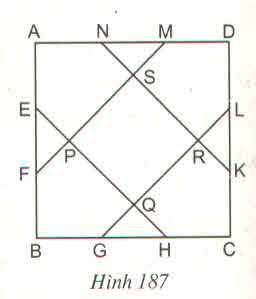
Hướng dẫn giải
Diện tích hình vuông \(ABCD\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích \(\Delta DKN\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích phần còn lại là: \(36-\left(8+8\right)=20\left(cm^2\right)\)
Trong \(\Delta\) vuông \(AEN\) ta có:
\(EN^2=AN^2+AE^2=4+4=8\)
\(EN=\sqrt{8}=2\sqrt{2}\left(cm\right)\)
Trong \(\Delta\) vuông \(BHE\) ta có:
\(EH^2=BE^2+BH^2=16+16=32\)
\(EH=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ENKH}=2\sqrt{2}\times4\sqrt{2}=16\left(cm^2\right)\)
Nối đường chéo \(BD\). Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật \(ENKH\) chia thành bốn phần bằng nhau nên \(S_{PQRS}\) chiếm 2 phần bằng \(8cm^2\) .
\(S_{AEPSN}=S_{AEN}+S_{EPSN}=2+\dfrac{16}{4}=6\left(cm^2\right)\)
Vậy............
Bài 3.1 - Bài tập bổ sung (Sách bài tập - trang 160)
a) Có thể dùng kéo cắt 2 lầ và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh đê rghesp lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó
Hướng dẫn giải


Bài 28 (Sách bài tập - trang 160)
Tính diện tích hình 186 theo kích thức đã cho trên hình (a, b, c có cùng đơn vị đo)
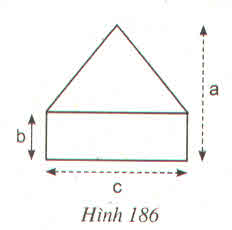
Hướng dẫn giải
Bài 3.2 - Bài tập bổ sung (Sách bài tập - trang 161)
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T
Chứng minh rằng MH + MK + MT không phụ thuộc vào vị trí của điểm M
Hướng dẫn giải

Bài 25 (Sách bài tập - trang 159)
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành 4 tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?
Hướng dẫn giải
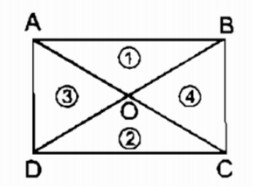
Gọi O là giao điểm hai đường chéo hình chữ nhật ABCD
⇒ OA = OB = OC = OD (tính chất hình chữ nhật)
∆ OAB = ∆ OCD (c.g.c) ⇒SOAB=SOCD⇒SOAB=SOCD (1)
∆ OAD = ∆ OBC (c.g.c) ⇒SOAD=SOBC⇒SOAD=SOBC (2)
Kẻ AH ⊥ BD
SOAD=\(\dfrac{1}{2}AH.OD\)
SOAB=\(\dfrac{1}{2}AH.OB\)
Suy ra: SOAD=SOAB (3)
Từ (1), (2) và (3) suy ra:
SOAB=SOBC=SOCD=SODA
Bài 26 (Sách bài tập - trang 159)
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi ?
Hướng dẫn giải
Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .
Bài 27 (Sách bài tập - trang 159)
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (\(d\perp BC\)). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC
a) Điền vào ô trống trong bảng sau :
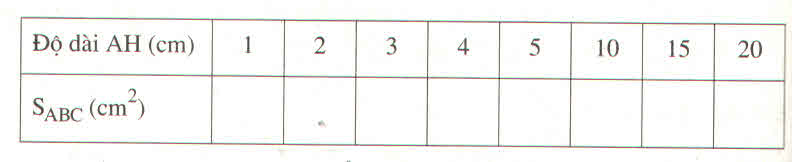
b) Vẽ đồ thị biểu diễn số đo \(S_{ABC}\) độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?




