Ôn tập chương Biểu thức đại số
Lý thuyết 
Mục lục
* * * * *
Bài 55 (Sách bài tập - tập 2 - trang 28)
Cho hai đa thức :
\(f\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(g\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
Tính : \(f(x) +g(x)\) và \(\text{f(x) - g(x)}\)
Hướng dẫn giải
f(x)=x5−3x2+7x4−9x3+x2−\(\dfrac{1}{4}\)x
=x5+7x4−9x3+2x2−\(\dfrac{1}{4}\)x
g(x)=5x4−x5+x2−2x3+3x2−\(\dfrac{1}{4}\)
=x5+5x4−2x3+4x2−\(\dfrac{1}{4}\)
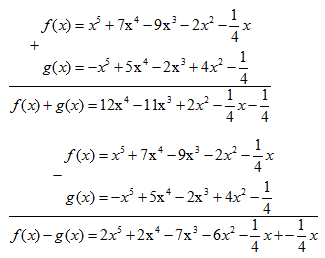
Bài 54 (Sách bài tập - tập 2 - trang 28)
Thu gọn các đơn thức sau rồi tìm hệ số của nó :
a) \(\left(-\dfrac{1}{3}xy\right).\left(3x^2yz^2\right)\)
b) \(-54y^2.bx\) (b là hằng số)
c) \(-2x^2y.\left(-\dfrac{1}{2}\right)^2.x\left(y^2z\right)^3\)
Hướng dẫn giải
a)
\(\left(-\dfrac{1}{3}xy\right).\left(3x^2yz^2\right)=\left(-\dfrac{1}{3}.3\right).\left(x.x^2\right).\left(y.y\right).z^2=-x^3y^2z^2\), có hệ số là -1.
b)
\(-54y^2.bx=\left(-54.b\right).x.y^2=-54bxy^2\), có hệ số là -54b.
c)
\(-2x^2y.\left(-\dfrac{1}{2}\right)^2.x\left(y^2z\right)^3=-2x^2y.\left(\dfrac{1}{4}xy^6z^3\right)=\left(-2.\dfrac{1}{4}\right).\left(x^2x\right).\left(yy^6\right).z^3=-\dfrac{1}{2}x^3y^7z^3\), có hệ số là \(-\dfrac{1}{2}\).
Bài 57 (Sách bài tập - tập 2 - trang 28)
Chọn số là nghiệm của đa thức :
Hướng dẫn giải
a)3
b)-1/6
c)-2
d)6
e)1/2
Bài 52 (Sách bài tập - tập 2 - trang 27)
Viết một biểu thức đại số chứa x, y thỏa mãn một trong các điều sau :
a) Là đơn thức
b) Chỉ là đa thức nhưng không phải là đơn thức
Hướng dẫn giải
a) xy
b) x + y
Bài 56 (Sách bài tập - tập 2 - trang 28)
Cho đa thức :
\(f\left(x\right)=-15x^3+5x^4-4x^2+8x^2-9x^3-x^4+15-7x^3\)
a) Thu gọn đa thức trên
b) Tính \(f\left(1\right);f\left(-1\right)\)
Hướng dẫn giải
a) f(x) = -15x3+5x4-4x2+8x2-9x3-x4+15-7x3
= (5x4-x4)-(15x3+9x3+7x3)+(8x2-4x2)+15
= 4x4-31x3+4x2+15
b) f(1)= 4.14-31.13+4.12+15 = -8
f(-1) = 4.(-1)4-31.(-1)3+4.(-1)2+15 = 54
Bài 53 (Sách bài tập - tập 2 - trang 27)
Hãy điền thêm một đơn thức vào ô trống để được tích của hai ô liền nhau là một đơn thức đồng dạng với đơn thức ở ô tương ứng :
Hướng dẫn giải
\(xy.5x=5x^2y\)
\(xy.13x^2y=15x^3y^2\)
\(xy.x\)\(=-x^2y\left(\Leftrightarrow x^2y\right)\)
\(xy.\)\(\dfrac{-y^2}{2}\)=\(\dfrac{-1}{2}xy^3\)
Bài 51 (Sách bài tập - tập 2 - trang 27)
Tính giá trị các biểu thức sau tại \(x=1;y=-1;z=3\)
a) \(\left(x^2y-2x-2z\right)xy\)
b) \(xyz+\dfrac{2x^2y}{y^2+1}\)
Hướng dẫn giải
a) Thế x = 1, y = -1, z = 3 vào biểu thức đã cho:
\(\left[1^2.\left(-1\right)-2.1-2.3\right]1.\left(-1\right)\)
= -9 . (-1)
= 9
Vậy biểu thức có giá trị bằng 9 tại x = 1, y = -1, z = 3.
b) Thế x = 1, y = -1, z = 3 vào biểu thức đã cho:
\(1.\left(-1\right).3+\dfrac{2.1^2.\left(-1\right)}{\left(-1\right)^2+1}\)
= -3 + \(\left(-1\right)\)
= -4
Vậy biểu thức có giá trị bằng -4 tại x = 1, y = -1, z = 3.
Có thể bạn quan tâm
Có thể bạn quan tâm
