Một số bài toán về đại lượng tỉ lệ thuận

Lý thuyết

Bài 13 (Sách bài tập - tập 1 - trang 67)

Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3 : 5 : 7. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi nếu tổng số tiền lãi là 450 triệu đồng và số tiền lại được chia tỉ lệ thuận với số vốn đã góp ?

Hướng dẫn giải

Đơn vị thứ nhất nhận được số tiền lãi là :

450:(3+5+7)x3=90 triệu đồng

Đơn vị thứ hai nhận được số tiền lãi là :

450:(3+5+7)x5=150 triệu đồng

​Đơn vị thứ ba nhận được số tiền lãi là :

450-150-90=210 triệu đồng

Đ/S:Đơn vị thứ nhất :90 triệu

Đơn vị thứ hai :150 triệu

​ Đơn vị thứ ba :210 triệu

Bài 17 (Sách bài tập - tập 1 - trang 67)

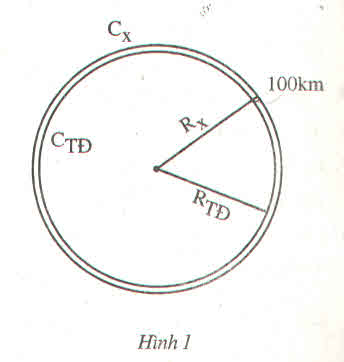
Đố vui :

Một kết quả bất ngờ. Biết rằng bán kính Trái Đất : \(R_{TĐ}\approx6370km\) (h.1). Giả sử một chiếc vệ tinh bay vòng quanh Trái Đất và cách mặt đất 100km

a) Em hãy dự đoán xem quãng đường vệ tinh bay một vòng dài hơn chu vi Trái Đất khoảng bao nhiêu km : Trên 1000km hay dưới 1000km

b) Em hãy tính cụ thể và cho biết kết quả 

Hướng dẫn giải

Bài 2.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 68)

Cho biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau. Gọi \(x_1,x_2\) là hai giá trị của x và \(y_1,y_2\) là hai giá trị tương ứng của y. Thay dấu ? bằng số thích hợp hợp trong bảng sau : 

\(x_1=3\)	\(y_1=?\)
\(x_2=?\)	\(y_2=?\)
\(x_1+x_2=2\)	\(y_1+y_2=10\)

 

 

 

Hướng dẫn giải

\(x_1=3\)	\(y_1=15\)
\(x_2=-1\)	\(y_2=-5\)
\(x_1+x_2=2\)	\(y_1+y_2=10\)

Bài 12 (Sách bài tập - tập 1 - trang 67)

Chu vi của một hình chữ nhật là 64 cm. Tính độ dài mỗi cạnh biết rằng chúng tỉ lệ với 3 và 5 ?

Hướng dẫn giải

Gọi a,b lần lượt là chiều dài và chiều rộng của hình chữ nhật

Ta có:(x+y).2=64

=> x+y = 64:2

=> x+y = 32

Theo đề bài ta có: x:y = 3:5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{3}=\dfrac{y}{5}\)và x+y = 32

=> \(\dfrac{x+y}{3+5}=\dfrac{32}{8}=4\)

Do đó: \(\dfrac{x}{3}=4\) => \(x=4.3\) => \(x=12\)

Bài 10 (Sách bài tập - tập 1 - trang 66)

Để làm nước mơ, người ta ngâm mơ theo công thức : 2kg mơ ngâm với 2,5 kg đường. Hỏi cần bao nhiêu kg đường để ngâm 5kg mơ ?

Hướng dẫn giải

Gọi x (kg) là khối lượng đường cần dùng để ngâm 5 (kg) mơ.

Vì khối lượng mơ tỉ lệ thuận với khối lượng đường nên ta có:

Vậy để ngâm 5kg mơ ta cần 6,25 kg đường.

Bài 2.1 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 68)

Trên một chiếc đồng hồ, khi kim giờ quay đúng 3 vòng thì số vòng kim phút quay được là :

(A) 15             (B) 36                      (C) 180                     (D) 2160

Hướng dẫn giải

B

Bài 11 (Sách bài tập - tập 1 - trang 66)

Biết rằng 17l dầu hỏa nặng 13,6 kg. Hỏi 12kg dầu hỏa có chứa được hết vào chiếc can 16 lít không ?

Hướng dẫn giải

Gọi x(lít) là số lít của 12kg dầu hỏa

Vì số lít dầu hỏa tỉ lệ thuận với khối lượng của nó nên ta có:

Vậy 12kg dầu hỏa đựng được hết vào chiếc can 16 lít.

Bài 15 (Sách bài tập - tập 1 - trang 67)

Tam giác ABC có số đo các góc A, B, C tỉ lệ 3 : 5 : 7. Tính số đo các góc của tam giác ABC (Biết rằng tổng số đo ba góc trong một tam giác bằng \(180^0\))

Hướng dẫn giải

Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được:

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)

\(\Rightarrow\widehat{A}=12^o.3=36^o\)

\(\widehat{B}=12^o.5=60^o\)

\(\widehat{C}=12^o.7=84^o\)

Bài 8 (Sách bài tập - tập 1 - trang 66)

Hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau không, nếu :

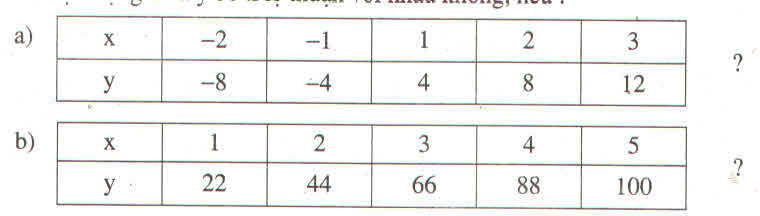
Hướng dẫn giải

a)\(\dfrac{-8}{-2}=\dfrac{-4}{-1}=\dfrac{4}{1}=\dfrac{8}{2}=\dfrac{12}{3}=4\)

Vậy hai đại lượng x và y ở bảng a) tỉ lệ thuận với nhau.

b) \(\dfrac{22}{1}\ne\dfrac{100}{5}\)

Vậy hai đại lượng x và y ở bảng b không tỉ lệ thuận với nhau.

Bài 16 (Sách bài tập - tập 1 - trang 67)

Gọi x, y, z theo thứ tự là số vòng quay của kim giờ, kim phút, kim giây trong cùng một thời gian 

a) Điền số thích hợp vào các ô trống trong hai bảng sau :

b) Viết công thức biểu diễn y theo x và z theo y

c) Số vòng quay x của kim giờ và số vòng quay z của kim giây có tỉ lệ thuận với nhau không ? Nếu có, hãy tìm số tỉ lệ của z đối với x

d) Khi kim giờ quay được 5 vòng thì kim giây quay được bao nhiêu vòng ?

Hướng dẫn giải

a)

x	1	2	3	4
y	12	24	36	48

y	1	6	12	18
z	60	360	720	1080

b) y = 12x; z = 60y

c) Ta có: z = 60. (12x) = 720x

Số vòng quay của kim giờ x và số vòng quay của kim giây z là hai đại lượng tỉ lệ thuận với nhau.

Hệ số tỉ lệ của z đối với x là 720

d) Thay x = 5 vào biểu thức z = 720x ta có:

z = 720. 5 = 3600(vòng)

Bài 2.3 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 68)

Cho \(x\) và \(y\) là hai đại lượng tỉ lệ thuận. Khi các giá trị \(x_1,x_2\) của \(x\) có tổng bằng 2 thì hai giá trị tương ứng là \(y_1,y_2\) có tổng bằng -10.

a) Hãy biểu diễn \(y\) theo \(x\)

b) Tính giá trị của \(y\) khi \(x=-1\)

Hướng dẫn giải

a) Vì x và y là hai đại lượng tỉ lệ thuận, nên :

y = ax (a là hệ số tỉ lệ, a khác 0)

Khi đó : \(\begin{cases} y_1 = ax_1\\ y_2 = ax_2 \end{cases}\)

Suy ra \(y_1+y_2=a\left(x_1+x_2\right)\) => -10 = a.2 => a = -5

Vậy : y = -5x

b) y = 5

Bài 14 (Sách bài tập - tập 1 - trang 67)

Biết độ dài các cạnh của một tam giác tỉ lệ với 3 : 4 : 5. Tính độ dài mỗi cạnh của tam giác đó biết cạnh lớn nhất dài hơn cạnh nhỏ nhất là 6m ?

Hướng dẫn giải

Gọi độ dài của các cạnh tam giác là a, b, c tỉ lệ với 3, 4, 5

Theo bài ra ta có:

\(a:b:c=3:4:5\) và c - a = 6

Áp dụng tính chất của dãy tỉ số bằng nhau:

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)

Do đó: \(\Rightarrow\left\{{}\begin{matrix}3.3=9\\4.3=12\\5.3=15\end{matrix}\right.\)

Vậy:...

Bài 9 (Sách bài tập - tập 1 - trang 66)

5 m dây đồng nặng 43 g. Hỏi 10 km dây đồng như thế nặng bao nhiêu kg ?

Hướng dẫn giải

Gọi x (g) là khối lượng của 10km dây đồng.

Ta có: 10km = 10000m

Vì khối lượng của dây đồng tỉ lệ thuận với chiều dài của dây nên ta có:

Suy ra: