Đại lượng tỷ lệ thuận
Bài 2 (Sách bài tập - tập 1 - trang 65)
Cho biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận. Điền các số thích hợp vào các ô trống trong bảng sau :
| \(x\) | \(-2\) | \(-1\) | \(1\) | \(3\) | \(4\) |
| \(y\) | \(2\) |
Hướng dẫn giải
Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
Bài 1.1 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 66)
Vì sao ta nói trong hình vuông chu vi tỉ lệ thuận với cạnh, còn diện tích thì không tỉ lệ thuận với cạnh ?
Hướng dẫn giải
chu vi tỉ lệ thuận với cạnh vì khi cạnh tăng thì chu vi tăng, cạnh giảm thì chu vi giảm và có hệ số tỉ lệ k luôn bằng 4 còn diện tích thì hệ số tỉ lệ k có thể thay dổi tùy theo đề bài
Bài 1.2 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 66)
Cho biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau khi \(x=-5\) thì \(y=\dfrac{1}{2}\)
Khi \(y=5\) thì giá trị tương ứng của \(x\) là :
(A) \(50\) (B) \(\dfrac{1}{50}\) (C) \(-50\) (D) \(-\dfrac{1}{50}\)
Hướng dẫn giải
Vì ta có y=k.x
Ta có x=-5 thì y=1/2
=> 1/2=k.-5
=>k=-1/10
Thay y=5, ta có :5=-1/10.x
=>x=-50
Bài 3 (Sách bài tập - tập 1 - trang 65)
Các giá trị tương ứng của \(t\) và \(s\) được cho trong bảng sau :
| \(t\) | 1 | 2 | 3 | 4 | 5 |
| \(s\) | 12 | 24 | 36 | 48 | 60 |
| \(\dfrac{t}{s}\) |
a) Điền các số thích hợp vào ô trống trong bảng trên
b) Hai đại lượng s và t có tỉ lệ thuận với nhau không ? Nếu có hãy tìm hệ số tỉ lệ ?
Hướng dẫn giải
a) Điền số thích hợp vào ô trống:
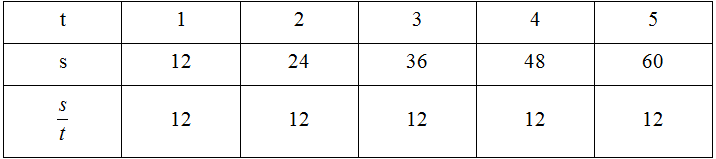
b) Hai đại lượng s và t tỉ lệ thuận vì s =12t, hệ số tỉ lệ bằng 12.
Bài 6 (Sách bài tập - tập 1 - trang 66)
Giá tiền của 8 gói kẹo là bao nhiêu, nếu biết rằng 6 gói kẹo giá 27 000 đồng ?
Hướng dẫn giải
Gọi x (đồng) là giá tiền của 8 gói kẹo .
Vì giá của mỗi gói kẹo không đổi nên số gói kẹo và số tiền mua tỉ lệ thuận với nhau.
Theo tính chất tỉ lệ thuận ta có: x8=270006x8=270006
Suy ra: x=27000×86=36000x=27000×86=36000
Vậy giá của 8 gói kẹo là 36.000 đồng
Bài 7 (Sách bài tập - tập 1 - trang 66)
Các giá trị tương ứng của t và s được cho trong bảng sau :
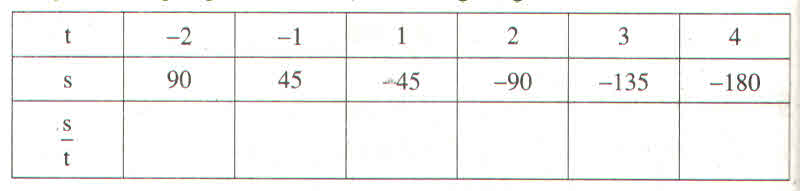
a) Điền các số thích hợp vào chỗ trống các ô trong bảng trên
b) Hai đại lượng s và t có tỉ lệ thuận với nhau hay không ? Nếu có hãy tìm hệ số tỉ lệ của s đối với t ?
Hướng dẫn giải
a)

b) s và t là hai đại lượng tỉ lệ thuận vì s = -45t
Hệ số tỉ lệ của s đối với t là -45
Bài 5 (Sách bài tập - tập 1 - trang 65)
Đố :
Em Vân của bạn Long đang lập bảng để chuẩn bị vẽ một biểu đồ hình cột :
| Số liệu | 360 | 460 | 520 | 640 | 700 |
| Chiều cao của cột (mm) | 18 | 23 | 32 |
Long bảo rằng trong bảng có chỗ sai
Vân ngạc nhiên hỏi : "Vì sao anh biết là sai khi anh chưa biết số liệu gì và em cũng chưa điền xong ?"
Long giải thích : "Chiều cao của các cột phải tỉ lệ thuận với các số liệu tương ứng"
Hãy sửa chỗ sai trong bảng và điền nốt các số đúng vào ô trống ?
Hướng dẫn giải
Chỗ sai trong bảng: 520 tương ứng với chiều cao là 32
Sai vì 36018=46023≠5203236018=46023≠52032. Phải sửa 32 thành 26.
Ta có bảng sau:
|
Số liệu |
360 |
460 |
520 |
640 |
700 |
|
Chiều cao của cột (mm) |
18 |
23 |
26 |
32 |
35 |
Bài 4 (Sách bài tập - tập 1 - trang 65)
Cho biết x tỉ lệ thuận với y theo hệ số tỉ lệ 0,8 và y tỉ lệ thuận với z theo hệ số tỉ lệ 5. Hãy chứng tỏ rằng x tỉ lệ thuận với z và tìm hệ số tỉ lệ ?
Hướng dẫn giải
Vì x tỉ lệ thuận với y theo hệ số tỉ lệ là 0,8 nên x = 0,8y (1)
y tỉ lệ thuận với z theo hệ số tỉ lệ là 5 nên y = 5z (2)
Thay (2) vào (1) ta có: x = 0,8y = 0,8y. (5z) = (0,8.5)z = 4z
Vậy x tỉ lệ thuận với z theo hệ số tỉ lệ là 4.
Bài 1 (Sách bài tập - tập 1 - trang 65)
Cho biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau và khi \(x=5\) thì \(y=3\)
a) Tìm hệ số tỉ lệ k của y đối với \(x\)
b) Hãy biểu diễn \(y\) theo \(x\)
c) Tính giá trị của \(y\) khi \(x=-5;x=10\)
Hướng dẫn giải
a) Ta có y tỉ lệ thuận với x theo hệ số tỉ lệ k nên y = kx mà khi x = 5 thì y = 3.
Suy ra: 3=k.5⇒k=353=k.5⇒k=35
b) y=35xy=35x
c) Khi x = -5 thì y=35.(−5)=−3y=35.(−5)=−3
Khi x = 10 thì y=35.10=6y=35.10=6




