Phương trình bậc nhất một ẩn và cách giải

Lý thuyết

• Bài 7 (Sgk tập 2 - trang 10)
• Bài 6 (Sgk tập 2 - trang 9)
• Bài 8 (Sgk tập 2 - trang 10)
• Bài 9 (Sgk tập 2 - trang 10)

Bài 7 (Sgk tập 2 - trang 10)

Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau :

a) \(1+x=0\)

b) \(x+x^2=0\)

c) \(1-2t=0\)

d) \(3y=0\)

e) \(0x-3=0\)

 

Hướng dẫn giải

Hướng dẫn giải:

Các phương trình là phương trình bậc nhất là:

1 + x = 0 ẩn số là x

1 - 2t = 0 ấn số là t

3y = 0 ẩn số là y

Bài 6 (Sgk tập 2 - trang 9)

Tính diện tích S của hình thang ABCD (h.1) theo x bằng hai cách :

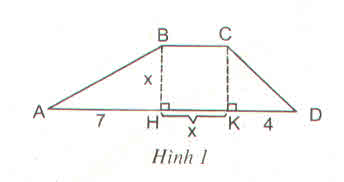
1) Theo công thức \(S=BH.\left(BC+DA\right):2\)

2) \(S=S_{ABH}+S_{BCKH}+S_{CKD}\)

Sau đó sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không ?

Hướng dẫn giải

Hướng dẫn giải:

Gọi S là diện tích hình thang ABCD.

1) Theo công thức

S = $\frac{BH(BC+DA)}{2}$

Ta có: AD = AH + HK + KD

=> AD = 7 + x + 4 = 11 + x

Do đó: S = $\frac{x(11+2x)}{2}$

2) Ta có: S = S_ABH + S_BCKH + S_CKD.

= $\frac{1}{2}$.AH.BH + BH.HK + $\frac{1}{2}$CK.KD

= $\frac{1}{2}$.7x + x.x + $\frac{1}{2}$x.4

= $\frac{7}{2}$x + x² + 2x

Vậy S = 20 ta có hai phương trình:

$\frac{x(11+2x)}{2}$ = 20 (1)

$\frac{7}{2}$x + x² + 2x = 20 (2)

Cả hai phương trình không có phương trình nào là phương trình bậc nhất.

Bài 8 (Sgk tập 2 - trang 10)

Giải các phương trình :

a) \(4x-20=0\)

b) \(2x+x+12=0\)

c) \(x-5=3-x\)

d) \(7-3x=9-x\)

Hướng dẫn giải

Hướng dẫn giải:

a) 4x - 20 = 0 <=> 4x = 20 <=> x = 5

Vậy phương trình có nghiệm duy nhất x = 5.

b) 2x + x + 12 = 0 <=> 2x + 12 = 0

<=> 3x = -12 <=> x = -4

Vậy phương trình đã cho có nghiệm duy nhất x = -4

c) x - 5 = 3 - x <=> x + x = 5 + 3

<=> 2x = 8 <=> x = 4

Vậy phương trình có nghiệm duy nhất x = 4

d) 7 - 3x = 9 - x <=> 7 - 9 = 3x - x

<=> -2 = 2x <=> x = -1

Vậy phương trình có nghiệm duy nhất x = -1.

Bài 9 (Sgk tập 2 - trang 10)

Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm :

a) \(3x-11=0\)

b) \(12+7x=0\)

c) \(10-4x=2x-3\)

Hướng dẫn giải