Các trường hợp bằng nhau của tam giác vuông

Lý thuyết

• Bài 63 (SGK tập 1 trang 136)
• Bài 64 (SGK tập 1 trang 136)
• Bài 65 (SGK tập 1 trang 136)
• Bài 66 (SGK tập 1 trang 136)

Bài 63 (SGK tập 1 trang 136)

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC \(\left(H\in BC\right)\). Chứng minh rằng :

a) HB = HC

b) \(\widehat{BAH}=\widehat{CAH}\)

Hướng dẫn giải

a) Hai tam giác vuông ABH và ACH có:

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(Câu a)

Suy ra ^BAH=^CAH(Hai góc tương ứng)

Bài 64 (SGK tập 1 trang 136)

Các tam giác vuông ABC và DEF có \(\widehat{A}=\widehat{D}=90^0\). AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau (về cạnh hay về góc) để \(\Delta ABC=\Delta DEF\) ?

Hướng dẫn giải

Các tam giác vuông ABC và DEF có $\hat{A}=\hat{D}={90}^0$. AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau (về cạnh hay về góc) đểΔABC=ΔDEF?

Giải:

Xem hình vẽ

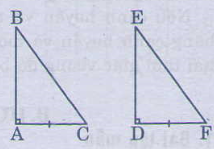
* Bổ sung thêm AB=DE

Thì ∆ABC=∆DEF (c.g.c)

* Bổ sung thêm $\hat{C}$=$\hat{F}$

Thì ∆ABC=∆DEF(g.c.g)

* Bổ sung thêm BC=EF

thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)

$\mathrm{\Delta }ABC=\mathrm{\Delta }DEF$

Bài 65 (SGK tập 1 trang 136)

Cho tam giác ABC cân tại A \(\left(\widehat{A}< 90^0\right)\). Vẽ \(BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right)\)

a) Chứng minh rằng AH = AK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là phân giác của góc A

Hướng dẫn giải

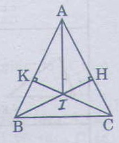
a) Hai tam giác vuông ABH và ACK có:

AB = AC(gt)

Góc A chung.

nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)

suy ra AH = AK.

b) Hai tam giác vuông AIK và AIH có:

AK = AH(cmt)

AI cạnh chung

Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)

Suy ra =

Vậy AI là tia phân giác của góc A.

Bài 66 (SGK tập 1 trang 136)

Tìm tam giác bằng nhau trên hình 148 :

                                 

Hướng dẫn giải

Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)

∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.

MD=ME, do ∆AMD=∆AME)

∆AMB= ∆AMC(Cạnh AM chung),

Cạnh MB=MC, cạnh AB=AC

Vì AD=AE, DB=EC