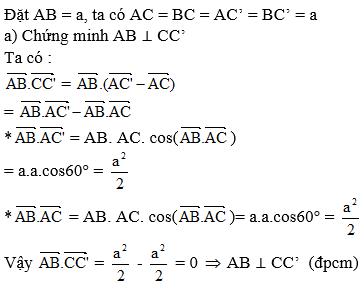Bài 2: Hai đường thẳng vuông góc

Lý thuyết

Bài 1 (SGK trang 97)

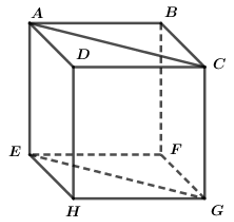
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây :

a) \(\overrightarrow{AB}\) và \(\overrightarrow{EG}\)

b) \(\overrightarrow{AF}\) và \(\overrightarrow{EG}\)

c) \(\overrightarrow{AB}\) và \(\overrightarrow{DH}\)

 

Hướng dẫn giải

Bài 2 (SGK trang 97)

Cho tứ diện ABCD

a) Chứng minh rằng \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\)

b) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có \(AB\perp CD\) và \(AC\perp DB\) thì \(AD\perp BC\)

 

Hướng dẫn giải

Bài 3 (SGK trang 97)

a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a và b có song song với nhau không ?

b) Trong không gian nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a có vuông góc với c không ?

Hướng dẫn giải

a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì nói chung a và b không song song với nhau vì a và b có thể cắt nhau hoặc có thể chéo nhau.

b) Trong không gian nếu a ⊥ b và b ⊥c thì a và c vẫn có thể cắt nhau hoặc chéo nhau do đó, nói chung a và c không vuông góc với nhau.

Bài 4 (SGK trang 98)

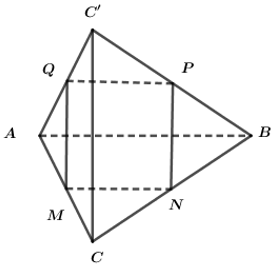
Trong không gian cho hai tam giác đều ABC và ABC' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC', C'A. Chứng minh rằng :

a) \(AB\perp CC'\)

b) Tứ giác MNPQ là hình chữ nhật 

Hướng dẫn giải

Bài 5 (SGK trang 98)

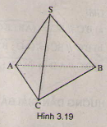
Cho hình chóp tam giác S.ABC có SA = Sb = SC và có \(\widehat{\:ASB}=\widehat{BSC}=\widehat{CSA}\). Chứng minh rằng \(SA\perp BC;SB\perp AC;SC\perp AB\) ?

Hướng dẫn giải

(h.3.19)

= SA.SC.cos - SA.SB.cos = 0.

Vậy SA ⊥ BC. 
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}\left(\overrightarrow{SC}-\overrightarrow{SA}\right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(=SB.SC.cos\widehat{BSC}-SB.SA.cos\widehat{BSA}=0\).
Vậy \(SB\perp AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.\left(\overrightarrow{SB}-\overrightarrow{SA}\right)=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(=SC.SB.cos\widehat{BSC}-SC.SA.cos\widehat{CSA}=0\).
Vậy \(SC\perp AB\).

Bài 6 (SGK trang 98)

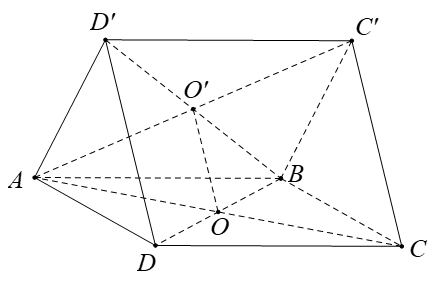
Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Chứng minh rằng \(AB\perp OO'\) và tứ giác CDD'C' là hình chữ nhật ?

Hướng dẫn giải

Bài 7 (SGK trang 98)

Cho S là diện tích của tam giác ABC. Chứng minh rằng :

                       \(S=\dfrac{1}{2}\sqrt{\overrightarrow{AB}^2.\overrightarrow{AC}^2-\left(\overrightarrow{AB}.\overrightarrow{AC}\right)^2}\)

Hướng dẫn giải

Bài 8 (SGK trang 98)

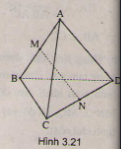
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^0\). Chứng minh rằng :

a) \(AB\perp CD\)

b) Nếu M, N lần lượt là trung điểm của AB và CD thì \(MN\perp AB\) và \(MN\perp CD\)

Hướng dẫn giải

Hướng dẫn.

(h.3.21)

a)

Suy ra

Ta có => AB ⊥ MN.

Chứng minh tương tự được CD ⊥ MN.