Bài 2: Giới hạn của hàm số

Lý thuyết

Mục lục

* * * * *

Bài 6 (SGK trang 133)

Tính :

a) $\lim\limits_{x\rightarrow+\infty}\left(x^4-x^2+x-1\right)$

b) $\lim\limits_{x\rightarrow-\infty}\left(-2x^3+3x^2-5\right)$

c) $\lim\limits_{x\rightarrow-\infty}\sqrt{x^2-2x+5}$

d) $\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}$

Hướng dẫn giải

a) (x⁴ – x² + x - 1) = x⁴(1 - ) = +∞.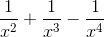

b) (-2x³ + 3x² -5 ) = x³(-2 + ) = +∞.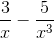

c) = = +∞.

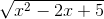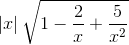d) $\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left|x\right|\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}$
$=\lim\limits_{x\rightarrow+\infty}\dfrac{x\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}$$=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}+1}{\dfrac{5}{x}-2}=-1$.

Bài 1 (SGK trang 132)

Dùng định nghĩa, tìm các giới hạn sau :

a) $\lim\limits_{x\rightarrow4}\dfrac{x+1}{3x-2}$

b) $\lim\limits_{x\rightarrow+\infty}\dfrac{2-5x^2}{x^2+3}$

Hướng dẫn giải

a) Hàm số f(x) = $\frac{x +1}{3x - 2}$ xác định trên R\{ $\frac{2}{3}$ } và ta có x = 4 ∈ ( $\frac{2}{3}$ ;+∞).

Giả sử (x_n) là dãy số bất kì và x_n ∈ ( $\frac{2}{3}$ ;+∞); x_n ≠ 4 và x_n→ 4 khi n→ +∞.

Ta có lim f(x_n) = lim $\frac{x_{n} +1}{3x_{n} - 2}$ = $\frac{4 + 1}{3. 4 - 2}$ = $\frac{1}{2}$ .

Vậy $\underset{x\rightarrow 4}{lim}$ $\frac{x +1}{3x - 2}$ = $\frac{1}{2}$ .

b) Hàm số f(x) = $\frac{2-5x^{2}}{x^{2}+3}$ xác định trên R.

Giả sử (x_n) là dãy số bất kì và x_n→ +∞ khi n→ +∞.

Ta có lim f(x_n) = lim $\frac{2-5x^{2}_{n}}{x^{2}_{n}+3}$ = lim $\frac{\frac{2}{x^{2}_{n}}-5}{1+\frac{3}{x^{2}_{n}}}$ = -5.

Vậy $\underset{x\rightarrow +\infty }{lim}$ $\frac{2-5x^{2}}{x^{2}+3}$ = -5.

Bài 2 (SGK trang 132)

Cho hàm số :

$f\left(x\right)=\left\{{}\begin{matrix}\sqrt{x}+1;x\ge0\\2x;x< 0\end{matrix}\right.$

và các dãy số $\left(u_n\right)$ với $\left(u_n\right)=\dfrac{1}{n},\left(v_n\right)$ với $v_n=-\dfrac{1}{n}$

Tính $\lim\limits u_n,\lim\limits v_n,\lim\limits f\left(u_n\right)$ và $\lim\limits f\left(v_n\right)$ ?

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x -> 0 ?

Hướng dẫn giải

$limu_n=lim\dfrac{1}{n}=0$; $limv_n=lim\left(-\dfrac{1}{n}\right)=0$.
$limf\left(u_n\right)=lim\left(\sqrt{\dfrac{1}{n}}+1\right)=1$.
$limf\left(v_n\right)=lim\left(2.\dfrac{-1}{n}\right)=lim\dfrac{-2}{n}=0$.
Hai dãy số $\left(u_n\right)$ và $\left(v_n\right)$ đều có giới hạn 0 khi n tiến ra dương vô cùng nhưng $limf\left(u_n\right)\ne limf\left(v_n\right)$ nên f không có giới hạn tại $x=0$.

Bài 4 (SGK trang 132)

Tìm các giới hạn sau :

a) $\lim\limits_{x\rightarrow2}\dfrac{3x-5}{\left(x-2\right)^2}$

b) $\lim\limits_{x\rightarrow1^-}\dfrac{2x-7}{x-1}$

c) $\lim\limits_{x\rightarrow1^+}\dfrac{2x-7}{x-1}$

Hướng dẫn giải

a) Ta có $\underset{x\rightarrow 2}{lim}$ (x - 2)²= 0 và (x - 2)²> 0 với ∀x ≠ 2 và $\underset{x\rightarrow 2}{lim}$ (3x - 5) = 3.2 - 5 = 1 > 0.

Do đó $\underset{x\rightarrow 2}{lim}$ $\frac{3x -5}{(x-2)^{2}}$ = +∞.

b) Ta có $\underset{x\rightarrow 1^{-}}{lim}$ (x - 1) và x - 1 < 0 với ∀x < 1 và $\underset{x\rightarrow 1^{-}}{lim}$ (2x - 7) = 2.1 - 7 = -5 <0.

Do đó $\underset{x\rightarrow 1^{-}}{lim}$ $\frac{2x -7}{x-1}$ = +∞.

c) Ta có $\underset{x\rightarrow 1^{+}}{lim}$ (x - 1) = 0 và x - 1 > 0 với ∀x > 1 và $\underset{x\rightarrow 1^{+}}{lim}$ (2x - 7) = 2.1 - 7 = -5 < 0.

Do đó $\underset{x\rightarrow 1^{+}}{lim}$ $\frac{2x -7}{x-1}$ = -∞.

Bài 3 (SGK trang 132)

Tính các giới hạn sau :

a) $\lim\limits_{x\rightarrow-3}\dfrac{x^2-1}{x+1}$

b) $\lim\limits_{x\rightarrow-2}\dfrac{4-x^2}{x+2}$

c) $\lim\limits_{x\rightarrow6}\dfrac{\sqrt{x+3}-3}{x-6}$

d) $\lim\limits_{x\rightarrow+\infty}\dfrac{2x-6}{4-x}$

e) $\lim\limits_{x\rightarrow+\infty}\dfrac{17}{x^2+1}$

f) $\lim\limits_{x\rightarrow+\infty}\dfrac{-2x^2+x-1}{3+x}$

Hướng dẫn giải

a) $\underset{x\rightarrow -3}{lim}$ $\frac{x^{2 }-1}{x+1}$ = $\frac{(-3)^{2}-1}{-3 +1}$ = -4.

b) $\underset{x\rightarrow -2}{lim}$ $\frac{4-x^{2}}{x + 2}$ = $\underset{x\rightarrow -2}{lim}$ $\frac{ (2-x)(2+x)}{x + 2}$ = $\underset{x\rightarrow -2}{lim}$ (2-x) = 4.

c) $\underset{x\rightarrow 6}{lim}$ $\frac{\sqrt{x + 3}-3}{x-6}$ = $\underset{x\rightarrow 6}{lim}$ $\frac{(\sqrt{x + 3}-3)(\sqrt{x + 3}+3 )}{(x-6) (\sqrt{x + 3}+3 )}$
= $\underset{x\rightarrow 6}{lim}$ $\frac{x +3-9}{(x-6) (\sqrt{x + 3}+3 )}$ = $\underset{x\rightarrow 6}{lim}$ $\frac{1}{\sqrt{x+3}+3}$ = $\frac{1}{6}$ .

d) $\underset{x\rightarrow +\infty }{lim}$ $\frac{2x-6}{4-x}$ = $\underset{x\rightarrow +\infty }{lim}$ $\frac{2-\frac{6}{x}}{\frac{4}{x}-1}$ = -2.

e) $\underset{x\rightarrow +\infty }{lim}$ $\frac{17}{x^{2}+1}$ = 0 vì $\underset{x\rightarrow +\infty }{lim}$ (x² + 1) = $\underset{x\rightarrow +\infty }{lim}$ x²( 1 + $\frac{1}{x^{2}}$ ) = +∞.

f) $\underset{x\rightarrow +\infty }{lim}$ $\frac{-2x^{2}+x -1}{3 +x}$ = $\underset{x\rightarrow +\infty }{lim}$ $\frac{-2+\frac{1}{x} -\frac{1}{x^{2}}}{\frac{3}{x^{2}} +\frac{1}{x}}$ = -∞, vì $\frac{3}{x^{2}}+\frac{1}{x}$ > 0 với ∀x>0.

Bài 5 (SGK trang 133)

Cho hàm số $f\left(x\right)=\dfrac{x+2}{x^2-9}$ có đồ thị như hình trên (Hình 53)

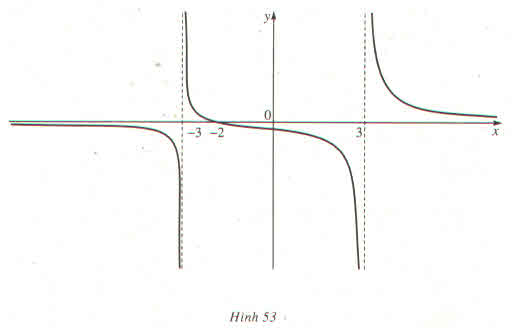
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi $x\rightarrow-\infty$, $x\rightarrow3^-,x\rightarrow-3^+$

b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau :

* $\lim\limits_{x\rightarrow-\infty}f\left(x\right)$ với $f\left(x\right)$ được xét trên khoảng $\left(-\infty;-3\right)$

* $\lim\limits_{x\rightarrow3^-}f\left(x\right)$ với $f\left(x\right)$ được xét trên khoảng $\left(-3;3\right)$

* $\lim\limits_{x\rightarrow-3^+}f\left(x\right)$ với $f\left(x\right)$ được xét trên khoảng $\left(-3;3\right)$

Hướng dẫn giải

Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3^-thì f(x) → -∞;

khi x → -3⁺thì f(x) x → +∞.

b) $\underset{x\rightarrow -\infty }{lim}$ f(x) = $\underset{x\rightarrow -\infty }{lim}$ $\frac{x+2}{x^{2}-9}$ = $\underset{x\rightarrow -\infty }{lim}$ $\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}}$ = 0.

$\underset{x\rightarrow 3^{-}}{lim}$ f(x) = $\underset{x\rightarrow 3^{-}}{lim}$ $\frac{x+2}{x^{2}-9}$ = $\underset{x\rightarrow 3^{-}}{lim}$ $\frac{x+2}{x+3}.\frac{1}{x-3}$ = -∞ vì $\underset{x\rightarrow 3^{-}}{lim}$ $\frac{x+2}{x+3}$ = $\frac{5}{6}$ > 0 và $\underset{x\rightarrow 3^{-}}{lim}$ $\frac{1}{x-3}$ = -∞.

$\underset{x\rightarrow -3^{+}}{lim}$ f(x) = $\underset{x\rightarrow -3^{+}}{lim}$ $\frac{x+2}{x^{2}-9}$ = $\underset{x\rightarrow -3^{+}}{lim}$ $\frac{x+2}{x-3}$ . $\frac{1}{x+3}$ = +∞
vì $\underset{x\rightarrow -3^{+}}{lim}$ $\frac{x+2}{x-3}$ = $\frac{-1}{-6}$ = $\frac{1}{6}$ > 0 và $\underset{x\rightarrow -3^{+}}{lim}$ $\frac{1}{x+3}$ = +∞.

Bài 7 (SGK trang 133)

Một thấu kinh hội tụ có tiêu cự là $f$. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB từ ảnh A'B' của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là : $\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}$

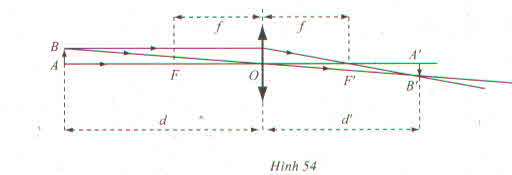
a) Tìm biểu thức xác định hàm số $d'=\varphi\left(d\right)$

b) Tìm $\lim\limits_{d\rightarrow f^+}\varphi\left(d\right);\lim\limits_{d\rightarrow f^-}\varphi\left(d\right)$ và $\lim\limits_{d\rightarrow+\infty}\varphi\left(d\right)$

Giải thích ý nghĩa của các kết quả tìm được ?

Hướng dẫn giải

a) Từ hệ thức $\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}.$ suy ra d' = φ(d) = $\frac{fd}{d-f}$ .

b) +) $\underset{d\rightarrow f^{+} }{lim}$ φ(d) = $\underset{d\rightarrow f^{+} }{lim}$ $\frac{fd}{d-f}$ = +∞ .

Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.

+) $\underset{d\rightarrow f^{-} }{lim}$ φ(d) = $\underset{d\rightarrow f^{-} }{lim}$ $\frac{fd}{d-f}$ = -∞.

Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.

+) $\underset{d\rightarrow +\infty }{lim}$ φ(d) = $\underset{d\rightarrow +\infty }{lim}$ $\frac{fd}{d-f}$ = $\underset{d\rightarrow +\infty }{lim}$ $\frac{f}{1-\frac{f}{d}}$ = f.

Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

Có thể bạn quan tâm

Hỏi đáp

MÔN HỌC

Bài 2: Giới hạn của hàm số

Bài 6 (SGK trang 133)

Hướng dẫn giải

Bài 1 (SGK trang 132)

Hướng dẫn giải

Bài 2 (SGK trang 132)

Hướng dẫn giải

Bài 4 (SGK trang 132)

Hướng dẫn giải

Bài 3 (SGK trang 132)

Hướng dẫn giải

Bài 5 (SGK trang 133)

Hướng dẫn giải

Bài 7 (SGK trang 133)

Hướng dẫn giải

Có thể bạn quan tâm

Có thể bạn quan tâm