§4. Các tập hợp số
Bài 1 (SGK trang 18)
Xác định các tập hợp sau và biểu diễn chúng trên trục số :
a. [ \(-3;1\)) \(\cup\) ( \(0;4\) ]
b. (\(0;2\) ] \(\cup\) [ \(-1;1\) )
c. \(\left(-2;15\right)\cup\left(3;+\infty\right)\)
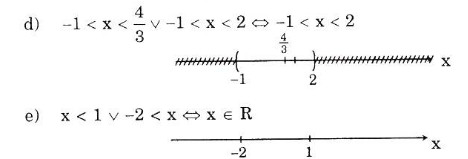
d. \(\left(-1;\dfrac{4}{3}\right)\cup\) [ \(-1;2\) )
e. \(\left(-\infty;1\right)\cup\left(-2;+\infty\right)\)
Hướng dẫn giải
a) [-3;1) ∪ (0;4] = [-3; 4]
![]()
b) (0; 2] ∪ [-1;1) = [-1; 2]
![]()
c) (-2; 15) ∪ (3; +∞) = (-2; +∞)
![]()
Bài 2 (SGK trang 18)
Xác định các tập hợp sau và biểu diễn chúng trên trục số :
a. ( \(-12;3\) ] \(\cap\) [ \(-1;4\) ]
b. \(\left(4;7\right)\cap\left(-7;-4\right)\)
c. \(\left(2;3\right)\cap\) [\(3;5\) )
d. ( \(-\infty;2\) ] \(\cap\) [ \(-2;+\infty\))
Hướng dẫn giải
a) (-12; 3] ∩ [-1; 4] = [-1; 3]
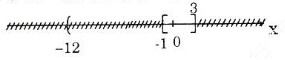
b) (4, 7) ∩ (-7; -4) = Ø

c) (2; 3) ∩ [3; 5) = Ø
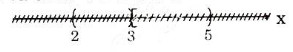
d) (-∞; 2] ∩ [-2; +∞)= [-2; 2].
![]()
Bài 3 (SGK trang 18)
Xác định các tập hợp sau và biểu diễn chúng trên trục số :
a. \(\left(-2;3\right)\) \ \(\left(1;5\right)\)
b. \(\left(-2;3\right)\) \ [ \(-2;+\infty\))
c. \(R\) \ \(\left(2;+\infty\right)\)
d. \(R\) \ ( \(-\infty;3\) ]
Hướng dẫn giải
a) (-2; 3)\ (1; 5) = (-2; 1];
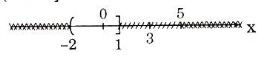
b) (-2; 3) \[1; 5) = (-2; 1);
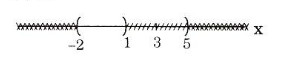
c) R\ (2; +∞) = (- ∞; 2]
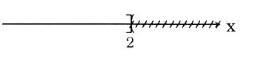
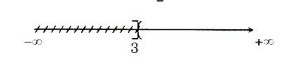
d) R \(-∞; 3] = (3; +∞).
Bài 28 (SBT trang 16)
Xác định mỗi tập hợp số sau và biểu diễn nó trên trục số :
a) \(\left(-3;3\right)\cup\left(-1;0\right)\)
b) \(\left(-1;3\right)\cup\) (\(0;5\)]
c) \(\left(-\infty;0\right)\cap\left(0;1\right)\)
d) ( \(-2;2\) ] \(\cap\) [ \(1;3\) )
Hướng dẫn giải

Bài 29 (SBT trang 16)
Cho \(a,b\in R,a< b\). Hãy xét quan hệ bao hàm \(\subset\) của các tập hợp sau :
a) \(A=\left[a;b\right]\)
b) \(B=\) ( \(a;b\)]
c) \(C=\) [ a; b)
d) \(D=\left(a;b\right)\)
Hướng dẫn giải
\(B\subset A,C\subset A,D\subset A,D\subset B,D\subset C\)
Bài 30 (SBT trang 16)
Xác định tập hợp \(A\cap B\) với :
a) \(A=\left[1;5\right];B=\left(-3;2\right)\cup\left(3;7\right)\)
b) \(\left(-5;0\right)\cup\left(3;5\right);B=\left(-1;2\right)\cup\left(4;6\right)\)
Hướng dẫn giải
a) \(A\cap B=\)[\(1;2\)) \(\cup\) (\(3;5\)]
b) \(A\cap B=\)\(\left(-1;0\right)\cup\left(4;5\right)\))
Bài 31 (SBT trang 16)
Xác định tính đúng, sai của mỗi mệnh đề sau :
a) \(\left[-3;0\right]\cap\left(0;5\right)=\left\{0\right\}\)
b) \(\left(-\infty;2\right)\cup\left(2;+\infty\right)=\left(-\infty;+\infty\right)\)
c) \(\left(-1;3\right)\cap\left(2;5\right)=\left(2;3\right)\)
d) \(\left(1;2\right)\cup\left(2;5\right)=\left(1;5\right)\)
Hướng dẫn giải
a) Sai;
b) Sai;
c) Đúng;
d) Sai;
Bài 32 (SBT trang 16)
Cho a, b, c, d là những số thực và \(a< b< c< d\)
Xác định các tập hợp số sau :
a) \(\left(a;b\right)\cap\left(c;d\right)\)
b) ( \(a;c\)] \(\cap\) [ \(b;d\))
c) \(\left(a;d\right)\)\ \(\left(b;c\right)\)
d) \(\left(b;d\right)\)\ \(\left(a;c\right)\)
Hướng dẫn giải
a) (a;b)∩(c;d)=∅(a;b)∩(c;d)=∅
b) (a;c]∩[b;d)=[b;c](a;c]∩[b;d)=[b;c]
c) (a;d)∖(b;c)=(a;b]∪[c;d)(a;d)∖(b;c)=(a;b]∪[c;d)
d) (b;d)∖(a;c)=[c;d)




