§4. Các tập hợp số
Bài 28 trang 16 Sách bài tập (SBT) Toán Đại số 10
Xác định mỗi tập hợp số sau và biểu diễn nó trên trục số
a) \(( - 3;3) \cup ( - 1;0)\)
b) \(( - \infty ;0) \cup (0;1)\)
c) \(( - 1;3) \cup {\rm{[0}};5{\rm{]}}\)
d) \(( - 2;2{\rm{]}} \cup {\rm{[}}1;3)\)
Hướng dẫn giải
a) \(( - 3;3) \cup ( - 1;0) = ( - 3;3)\)
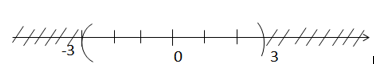
b) \(( - 1;3) \cup {\rm{[0}};5{\rm{] = ( - 1;5]}}\)

c) \(( - \infty ;0) \cup (0;1) = \emptyset \)
![]()
d) \(( - 2;2{\rm{]}} \cup {\rm{[}}1;3) = {\rm{(}}-2;3)\)
Bài 29 trang 16 Sách bài tập (SBT) Toán Đại số 10
Cho \(a,b \in R,a < b\) . Hãy xét quan hệ bào hàm \( \subset \) của các tập hợp sau:
a) \(A = {\rm{[}}a;b{\rm{]}}\)
b) \(B = (a;b{\rm{]}}\)
c) \(C = {\rm{[}}a;b)\)
d) \(D = (a;b)\)
Hướng dẫn giải
\(B \subset A,C \subset A,D \subset A,D \subset B,D \subset C\)
Bài 30 trang 16 Sách bài tập (SBT) Toán Đại số 10
Xác định tập hợp \(A \cap B\), với:
a) \(A = {\rm{[1;5]; B = ( - 3;2)}} \cup {\rm{(3;7);}}\)
b) \(A = ( - 5;0) \cup {\rm{ (3;5);B = ( - 1;2)}} \cup {\rm{(4;6)}}{\rm{.}}\)
Hướng dẫn giải
a) \(A \cap B = {\rm{[}}1;2) \cup (3;5]\)
b) \(A \cap B = ( - 1;0) \cup (4;5)\)
Bài 31 trang 16 Sách bài tập (SBT) Toán Đại số 10
Xác định tính đúng, sai của mỗi mệnh đề sau
a) \({\rm{[1;5]}} \cap {\rm{ (0;5)}} = {\rm{\{ }}0\} \)
b) \({\rm{( - 1;3)}} \cap {\rm{ (2;5)}} = (2;3)\)
c) \(( - \infty ;2) \cup (2; + \infty ) = ( - \infty ; + \infty )\)
d) \((1;2) \cup (2;5) = (1;5)\)
Hướng dẫn giải
a) Sai;
b) Đúng;
c) Sai;
d) Sai;
Bài 32 trang 16 Sách bài tập (SBT) Toán Đại số 10
Cho a, b, c, d là những số thực và a < b < c < d. Xác định các tập hợp số sau:
a) \((a;b) \cap (c;d)\);
b) \((a;d)\backslash (b;c)\);
c) \((a;c{\rm{]}} \cap {\rm{[b}};d)\);
d) \((b;d) \cap (a;c)\);
Hướng dẫn giải
a) \((a;b) \cap (c;d) = \emptyset \)
b) \((a;c{\rm{]}} \cap {\rm{[}}b;d) = {\rm{[}}b;c{\rm{]}}\)
c) \((a;d)\backslash (b;c) = (a;b{\rm{]}} \cup {\rm{[}}c;d)\)
d) \((b;d)\backslash (a;c) = {\rm{[}}c;d)\)




