Đề thi học kì 2 Toán 12 trường THCS-THPT Chi Lăng năm 2020-2021
Nội dung tài liệu
Tải xuốngCác tài liệu liên quan
-
![Đề thi học kì 2 môn Sinh học lớp 12 năm học 2017 - 2018 trường THPT Tiến Thịnh - Hà Nội]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 1]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 20]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 19]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 18]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 17]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 14]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 16]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 15]()
-
![Đề thi học kì 1 Toán 12 năm 2015-2016 ĐỀ THAM KHẢO SỐ 13]()
Có thể bạn quan tâm
Thông tin tài liệu
TRƯỜNG THCS& THPT CHI LĂNG ĐỀ MINH HỌA |
ĐỀ KIỂM TRA CUỐI KÌ 2 NĂM HỌC 2020-2021 Môn : TOÁN, Lớp 12 Thời gian làm bài: 90 phút không tính thời gian phát đề |
|---|
Họ và tên học sinh:…………………………………... Mã số học sinh:………………………….
I.TRẮC NGHIỆM
Câu 1: (NB) Hàm số nào trong các hàm số sau đây là
một nguyên hàm của hàm số 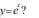
A. 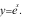 B.
B. 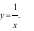 C.
C. 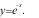 D.
D. 
Câu 2: (NB) Cho  Khi đó với
Khi đó với  ta
có
ta
có  bằng?
bằng?
A.  B.
B.  C.
C.  D.
D. 
Câu 3: (TH) Tìm họ nguyên hàm của hàm số 
A.  B.
B. 
C.  D.
D. 
Câu 4: (TH) Biết một nguyên hàm của hàm số 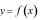 là
là 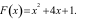 Khi
đó, giá trị của hàm số
Khi
đó, giá trị của hàm số 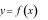 tại
tại
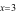 là:
là:
A. 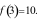 B.
B. 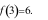 C.
C. 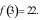 D.
D. 
Câu 5: (NB) Cho hai hàm số 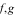 liên tục trên đoạn
liên tục trên đoạn  và số thực
và số thực 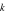 tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
A. 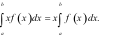 B.
B. 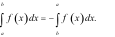
C. 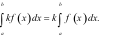 D.
D. 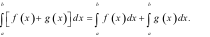
Câu 6: (NB) 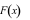 là một nguyên hàm của
là một nguyên hàm của  Công thức nào sau đây đúng?
Công thức nào sau đây đúng?
A. 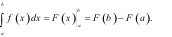 B.
B. 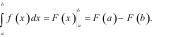
C. 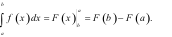 D.
D. 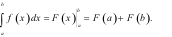
Câu 7: (TH) Cho  và
và  Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
A.  B.
B.  C.
C.  D.
D. 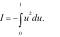
Câu 8: (TH) Hàm số 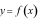 liên tục trên
liên tục trên  là
một nguyên hàm của hàm số
là
một nguyên hàm của hàm số 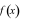 trên
trên  và
và 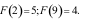 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
A.  B.
B.  C.
C.  D.
D. 
Câu 9: (NB) Cho hàm số 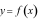 xác định và liên tục trên đoạn
xác định và liên tục trên đoạn  Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số  trục hoành và hai đường thẳng
trục hoành và hai đường thẳng  được tính theo công thức?
được tính theo công thức?
A.  B.
B.  C.
C. 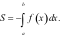 D.
D. 
Câu 10: (NB) Cho hai hàm số 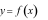 và
và 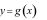 liên tục trên
liên tục trên  Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 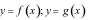 và các đường thẳng
và các đường thẳng  bằng?
bằng?
A.  B.
B. 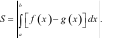
C.  D.
D. 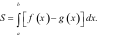
Câu 11: (NB) Cho hàm số 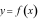 liên tục trên đoạn
liên tục trên đoạn  Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số  trục hoành và hai đường thẳng
trục hoành và hai đường thẳng  Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được
tính theo công thức:
Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được
tính theo công thức:
A. 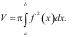 B.
B.  C.
C. 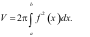 D.
D. 
Câu 12: (TH) Gọi S là diện tích hình phẳng giới hạn
bởi đồ thị hàm số  trục hoành, các đường thẳng
trục hoành, các đường thẳng  (như hình vẽ bên). Hỏi cách tích S nào dưới đây đúng?
(như hình vẽ bên). Hỏi cách tích S nào dưới đây đúng?
A.  B.
B. 
C.  D.
D. 
Câu 13: (TH) Tính thể tích của vật thể tròn xoay khi
quay hình phẳng giới hạn bởi các đường  quay quanh trục Ox.
quay quanh trục Ox.
A.  B.
B.  C.
C.  D.
D. 
Câu 14:(NB) Cho số phức  Phần ảo của số phức z là :
Phần ảo của số phức z là :
A. 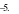 B.
B.  C.
C.  D.
D. 
Câu 15: (NB) Cho số phức  Điểm biểu diễn hình học của số phức
Điểm biểu diễn hình học của số phức  là:
là:
A.  B.
B.  C.
C.  D.
D. 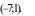
Câu 16: (NB) Cho hai số phức 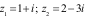 .
Khi đó
.
Khi đó 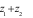 bằng:
bằng:
A.  B.
B.  C.
C.  D.
D. 
Câu 17: (NB) Cho hai số phức  và số phức
và số phức  ; (với
; (với  là số thực). Tìm phần ảo của số phức
là số thực). Tìm phần ảo của số phức 
A.  B.
B.  C.
C.  D.
D. 
Câu 18: (NB) Cho hai số phức  và số phức
và số phức  . Khi đó phần thực của số phức
. Khi đó phần thực của số phức  bằng:
bằng:
A.  B.
B.  C.
C.  D.
D. 
Câu 19: (NB) Cho số phức  . Tính
. Tính 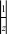
A B.
B. 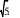 C.
C.  D.
D. 
Câu 20: (NB) Trên tập số phức. Phương trình nào sau
đây nhận 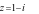 làm nghiệm?
làm nghiệm?
A.  B.
B.  C.
C. 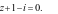 D.
D. 
Câu 21: (TH) Số thực x,y thỏa mãn  là:
là:
A. 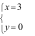 .
B.
.
B. .
C.
.
C. .
D.
.
D. .
.
Câu 22: (TH) Cho số phức 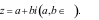 Số phức
Số phức 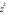 có phần thực là:
có phần thực là:
A. 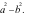 B.
B. 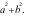 C.
C.  D.
D. 
Câu 23:(TH) Số phức  có mođun bằng
có mođun bằng 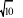 khi
khi
A. 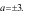 B.
B. 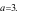 C.
C.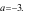 D.
D. 
Câu 24: (TH) Cho số phức z thỏa mãn  .
Giá trị của biểu thức
.
Giá trị của biểu thức 
A. 13. B. 12. C. 14. D. 15.
Câu 25: (TH) Trên tập hợp số phức  ,
gọi
,
gọi  là hai nghiệm phức của phương trình
là hai nghiệm phức của phương trình 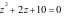 .
Tính giá trị của biểu thức
.
Tính giá trị của biểu thức 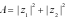 .
.
A.
B.
C.
D
Câu 26:(NB) Trong không gian 
 ,
tọa độ điểm M là.
,
tọa độ điểm M là.
A.  B.
B.  C.
C.  D.
D. 
Câu 27:(TH) Trong không gian  ,
cho hai điểm
,
cho hai điểm  và
và  ,
khoảng cách giữa hai điểm A và B là.
,
khoảng cách giữa hai điểm A và B là.
A. 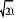 B.
B. 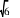 C.
C.  D.
D. 
Câu 28:(NB) Trong không gian  ,
cho mặt phẳng (P):-3x+z-5=0, điểm nào sau đây thuộc mặt phẳng (P).
,
cho mặt phẳng (P):-3x+z-5=0, điểm nào sau đây thuộc mặt phẳng (P).
A.  B.
B.  C.
C.  D.
D. 
Câu 29:(NB) Trong không gian Oxyz, cho hai mặt phẳng
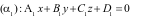 và
và
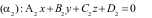 có
hai vectơ pháp tuyến lần lượt là
có
hai vectơ pháp tuyến lần lượt là  ,
điều kiện để
,
điều kiện để 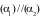 là.
là.
A.  B.
B.  C.
C.  D.
D. 
Câu 30:(TH) Trong không gian  ,
mặt phẳng (P) chứa hai vectơ
,
mặt phẳng (P) chứa hai vectơ 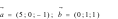 ,
mặt phẳng (P) có một vectơ pháp tuyến là.
,
mặt phẳng (P) có một vectơ pháp tuyến là.
A.  B.
B.  C.
C. 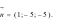 D.
D. 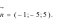
Câu 31:(TH) Trong không gian  ,
cho A(1;1;-1) và mặt phẳng (P): x-5y-1=0. khoảng cách từ A tới mặt phẳng
(P) bằng .
,
cho A(1;1;-1) và mặt phẳng (P): x-5y-1=0. khoảng cách từ A tới mặt phẳng
(P) bằng .
A. 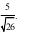 B.
B. 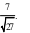 C.
C. 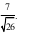 D.
D. 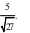
Câu 32:(NB) Trong không gian  ,
cho đường thẳng d:
,
cho đường thẳng d:  ,
điểm nào sau đây thuộc đường thẳng d.
,
điểm nào sau đây thuộc đường thẳng d.
A.  B.
B.  C.
C.  D.
D. 
Câu 33:(NB) Trong không gian  ,
phương trình tham số của đường thẳng d đi qua điểm
,
phương trình tham số của đường thẳng d đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương 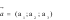 là phương trình có dạng.
là phương trình có dạng.
A.  B.
B.  C.
C.  D.
D. 
Câu 34:(NB) Trong không gian  ,
gọi
,
gọi 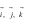 lần lượt là các vectơ đơn vị trên các trục x’Ox, y’Oy, z’Oz. Trục x’Ox
có một vectơ chỉ phương là.
lần lượt là các vectơ đơn vị trên các trục x’Ox, y’Oy, z’Oz. Trục x’Ox
có một vectơ chỉ phương là.
A.  B.
B.  C.
C.  D.
D. 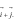
Câu 35:(TH) Trong không gian  ,
Cho đường thẳng d:
,
Cho đường thẳng d:  đường
thẳng d có một vectơ chỉ phương là.
đường
thẳng d có một vectơ chỉ phương là.
A. 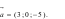 B.
B. 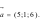 C.
C. 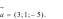 D.
D. 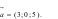
II.TỰ LUẬN
Câu 1: Tính tích phân 
Câu 2:Trong không gian Oxyz, cho đường thẳng (d) có
phương trình  và mặt phẳng (P) có phương trình
và mặt phẳng (P) có phương trình  .
Viết phương trình mặt cầu (S) có tâm I thuộc (d), bán kính
.
Viết phương trình mặt cầu (S) có tâm I thuộc (d), bán kính  và tiếp xúc với mặt phẳng (P).
và tiếp xúc với mặt phẳng (P).
Câu 3: Một ô tô bắt đầu chuyển động nhanh dần đều
với vận tốc  .
Đi được
.
Đi được 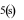 ,
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục
chuyển động chậm dần đều với gia tốc
,
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục
chuyển động chậm dần đều với gia tốc 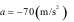 .
Tính quãng đường
.
Tính quãng đường 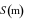 đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
Câu 4:Cho Z là số phức có mô đun bằng 2021 và W là
số phức thỏa mãn  . Tìm mô đun số phức W.
. Tìm mô đun số phức W.
------------- HẾT -------------
TRƯỜNG THCS& THPT CHI LĂNG ĐÁP ÁN ĐỀ MINH HỌA |
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CUỐI KỲ II NĂM HỌC 2020 - 2021 Môn : TOÁN, Lớp 12 |
|---|
I.PHẦN TRẮC NGHIỆM
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Đáp án | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A |
| Câu | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | ||
| Đáp án | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | ||
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
ĐÁP ÁN CHI TIẾT PHẦN TRẮC NGHIỆM
Câu 1: (NB) Hàm số nào trong các hàm số sau đây là
một nguyên hàm của hàm số 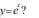
A. 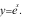 B.
B. 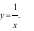 C.
C. 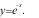 D.
D. 
=> theo công thức . đáp án là A
Câu 2: (NB) Cho  Khi đó với
Khi đó với  ta
có
ta
có  bằng?
bằng?
A.  B.
B.  C.
C.  D.
D. 
=> theo công thức . đáp án là A
Câu 3: (TH) Tìm họ nguyên hàm của hàm số 
A.  B.
B. 
C.  D.
D. 
Ta có  đáp án là A
đáp án là A
Câu 4: (TH) Biết một nguyên hàm của hàm số 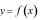 là
là 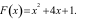 Khi
đó, giá trị của hàm số
Khi
đó, giá trị của hàm số 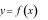 tại
tại
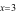 là:
là:
A. 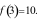 B.
B. 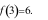 C.
C. 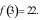 D.
D. 
Ta có 
Đáp án A.
Câu 5: (NB) Cho hai hàm số 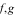 liên tục trên đoạn
liên tục trên đoạn  và số thực
và số thực 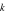 tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
tùy ý. Trong các khẳng định sau, khẳng định nào
sai?
A. 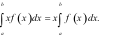 B.
B. 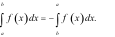
C. 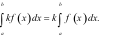 D.
D. 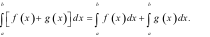
Đáp án A.
Câu 6: (NB) 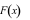 là một nguyên hàm của
là một nguyên hàm của  Công thức nào sau đây đúng?
Công thức nào sau đây đúng?
A. 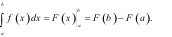 B.
B. 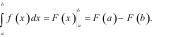
C. 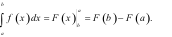 D.
D. 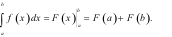
Đáp án A.
Câu 7: (TH) Cho  và
và  Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
A.  B.
B.  C.
C.  D.
D. 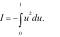
Đặt

 =>đáp án A
=>đáp án A
Câu 8: (TH) Hàm số 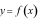 liên tục trên
liên tục trên  là
một nguyên hàm của hàm số
là
một nguyên hàm của hàm số 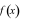 trên
trên  và
và 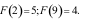 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
A.  B.
B.  C.
C.  D.
D. 
Ta có đáp án A
đáp án A
Câu 9: (NB) Cho hàm số 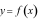 xác định và liên tục trên đoạn
xác định và liên tục trên đoạn  Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số  trục hoành và hai đường thẳng
trục hoành và hai đường thẳng  được tính theo công thức?
được tính theo công thức?
A.  B.
B.  C.
C. 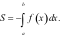 D.
D. 
=> theo công thức . đáp án là A
Câu 10: (NB) Cho hai hàm số 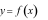 và
và 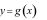 liên tục trên
liên tục trên  Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Diện tích hình phẳng giới hạn bởi đồ thị hàm số 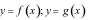 và các đường thẳng
và các đường thẳng  bằng?
bằng?
A.  B.
B. 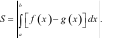
C.  D.
D. 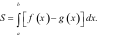
=> theo công thức . đáp án là A
Câu 11: (NB) Cho hàm số 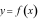 liên tục trên đoạn
liên tục trên đoạn  Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số  trục hoành và hai đường thẳng
trục hoành và hai đường thẳng  Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được
tính theo công thức:
Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được
tính theo công thức:
A. 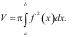 B.
B.  C.
C. 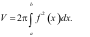 D.
D. 
=> theo công thức . đáp án là A
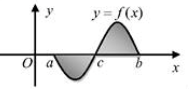
Câu 12: (TH) Gọi S là diện tích hình phẳng giới hạn
bởi đồ thị hàm số  trục hoành, các đường thẳng
trục hoành, các đường thẳng  (như hình vẽ bên). Hỏi cách tích S nào dưới đây đúng?
(như hình vẽ bên). Hỏi cách tích S nào dưới đây đúng?
A.  B.
B. 
C.  D.
D. 
=> nhìn vào đồ thị . đáp án là A
Câu 13: (TH) Tính thể tích của vật thể tròn xoay khi
quay hình phẳng giới hạn bởi các đường  quay quanh trục Ox.
quay quanh trục Ox.
A.  B.
B.  C.
C.  D.
D. 
Ta có  đáp án A
đáp án A
Câu 14:(NB) Cho số phức  Phần ảo của số phức z là :
Phần ảo của số phức z là :
A. 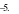 B.
B.  C.
C.  D.
D. 
đáp án A
Câu 15: (NB) Cho số phức  Điểm biểu diễn hình học của số phức
Điểm biểu diễn hình học của số phức  là:
là:
A.  B.
B.  C.
C.  D.
D. 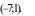
đáp án A
Câu 16: (NB) Cho hai số phức 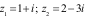 .
Khi đó
.
Khi đó 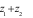 bằng:
bằng:
A.  B.
B.  C.
C.  D.
D. 
đáp án A
Câu 17: (NB) Cho hai số phức  và số phức
và số phức  ; (với
; (với  là số thực). Tìm phần ảo của số phức
là số thực). Tìm phần ảo của số phức 
A.  B.
B.  C.
C.  D.
D. 
Ta có  =>
đáp án A
=>
đáp án A
Câu 18: (NB) Cho hai số phức  và số phức
và số phức  . Khi đó phần thực của số phức
. Khi đó phần thực của số phức  bằng:
bằng:
A.  B.
B.  C.
C.  D.
D. 
Ta có  => đáp án A
=> đáp án A
Câu 19: (NB) Cho số phức  . Tính
. Tính 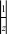
A B.
B. 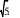 C.
C.  D.
D. 
Ta có
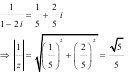
Đáp án A
Câu 20: (NB) Trên tập số phức. Phương trình nào sau
đây nhận 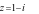 làm nghiệm?
làm nghiệm?
A.  B.
B.  C.
C. 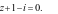 D.
D. 
Giải 4 pt ở 4 đáp án nếu có nghiệm z=1-i thì ta nhận. đáp án A
Câu 21: (TH) Số thực x,y thỏa mãn  là:
là:
A. 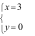 .
B.
.
B. .
C.
.
C. .
D.
.
D. .
.
Ta có
 .
Đáp án A
.
Đáp án A
Câu 22: (TH) Cho số phức 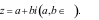 Số phức
Số phức 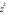 có phần thực là:
có phần thực là:
A. 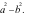 B.
B. 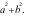 C.
C.  D.
D. 
Ta có  .
Đáp án A
.
Đáp án A
Câu 23:(TH) Số phức  có mođun bằng
có mođun bằng 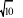 khi
khi
A. 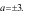 B.
B. 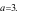 C.
C.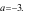 D.
D. 
Ta có
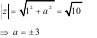 .
Đáp án A
.
Đáp án A
Câu 24: (TH) Cho số phức z thỏa mãn  .
Giá trị của biểu thức
.
Giá trị của biểu thức 
A. 13. B. 12. C. 14. D. 15.
Ta có  .
Đáp án A
.
Đáp án A
Câu 25: (TH) Trên tập hợp số phức  ,
gọi
,
gọi  là hai nghiệm phức của phương trình
là hai nghiệm phức của phương trình 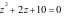 .
Tính giá trị của biểu thức
.
Tính giá trị của biểu thức 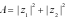 .
.
A.
B.
C.
D
Ta có  Đáp án A
Đáp án A
Câu 26:(NB) Trong không gian 
 ,
tọa độ điểm M là.
,
tọa độ điểm M là.
A.  B.
B.  C.
C.  D.
D. 
Đáp án A
Câu 27:(TH) Trong không gian  ,
cho hai điểm
,
cho hai điểm  và
và  ,
khoảng cách giữa hai điểm A và B là.
,
khoảng cách giữa hai điểm A và B là.
A. 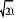 B.
B. 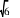 C.
C.  D.
D. 
Ta có
 Đáp án A
Đáp án A
Câu 28:(NB) Trong không gian  ,
cho mặt phẳng (P):-3x+z-5=0, điểm nào sau đây thuộc mặt phẳng (P).
,
cho mặt phẳng (P):-3x+z-5=0, điểm nào sau đây thuộc mặt phẳng (P).
A.  B.
B.  C.
C.  D.
D. 
Đáp án A
Câu 29:(NB) Trong không gian Oxyz, cho hai mặt phẳng
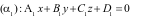 và
và
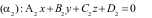 có
hai vectơ pháp tuyến lần lượt là
có
hai vectơ pháp tuyến lần lượt là  ,
điều kiện để
,
điều kiện để 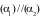 là.
là.
A.  B.
B.  C.
C.  D.
D. 
Đáp án A
Câu 30:(TH) Trong không gian  ,
mặt phẳng (P) chứa hai vectơ
,
mặt phẳng (P) chứa hai vectơ 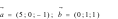 ,
mặt phẳng (P) có một vectơ pháp tuyến là.
,
mặt phẳng (P) có một vectơ pháp tuyến là.
A.  B.
B.  C.
C. 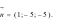 D.
D. 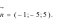
Ta có  .
Đáp án A
.
Đáp án A
Câu 31:(TH) Trong không gian  ,
cho A(1;1;-1) và mặt phẳng (P): x-5y-1=0. khoảng cách từ A tới mặt phẳng
(P) bằng .
,
cho A(1;1;-1) và mặt phẳng (P): x-5y-1=0. khoảng cách từ A tới mặt phẳng
(P) bằng .
A. 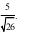 B.
B. 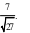 C.
C. 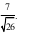 D.
D. 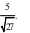
Ta có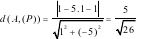 .
Đáp án A
.
Đáp án A
Câu 32:(NB) Trong không gian  ,
cho đường thẳng d:
,
cho đường thẳng d:  ,
điểm nào sau đây thuộc đường thẳng d.
,
điểm nào sau đây thuộc đường thẳng d.
A.  B.
B.  C.
C.  D.
D. 
Đáp án A
Câu 33:(NB) Trong không gian  ,
phương trình tham số của đường thẳng d đi qua điểm
,
phương trình tham số của đường thẳng d đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương 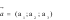 là phương trình có dạng.
là phương trình có dạng.
A.  B.
B.  C.
C.  D.
D. 
Đáp án A
Câu 34:(NB) Trong không gian  ,
gọi
,
gọi 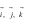 lần lượt là các vectơ đơn vị trên các trục x’Ox, y’Oy, z’Oz. Trục x’Ox
có một vectơ chỉ phương là.
lần lượt là các vectơ đơn vị trên các trục x’Ox, y’Oy, z’Oz. Trục x’Ox
có một vectơ chỉ phương là.
A.  B.
B.  C.
C.  D.
D. 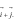
Đáp án A
Câu 35:(TH) Trong không gian  ,
Cho đường thẳng d:
,
Cho đường thẳng d:  đường
thẳng d có một vectơ chỉ phương là.
đường
thẳng d có một vectơ chỉ phương là.
A. 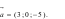 B.
B. 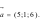 C.
C. 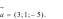 D.
D. 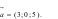
Đáp án A
II. PHẦN TỰ LUẬN
| Câu | Nội dung đáp án | Điểm | |||
|---|---|---|---|---|---|
| 1(1điểm) |  |
||||
Đặt Đổi cận
|
0.25 | ||||
 |
0.25 | ||||
Đặt  |
0.25 | ||||
 . . |
0.25 | ||||
2(1điểm) 2(1điểm) |
Viết phương trình mặt cầu (S) có tâm I thuộc (d), bán kính và tiếp xúc với mặt phẳng (P). | ||||
Xét 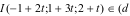 ,
ta có ,
ta có  |
0.25 | ||||
Do (S) tiếp xúc (P) và có bán kính  nên
nên  |
0.25 | ||||
 |
0.25 | ||||
Vậy có hai mặt cầu thoả đề bài là
|
0.25 | ||||
| 3(0.5điểm) | Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc  .
Đi được .
Đi được 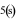 ,
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục
chuyển động chậm dần đều với gia tốc ,
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục
chuyển động chậm dần đều với gia tốc 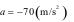 .
Tính quãng đường .
Tính quãng đường 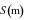 đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. |
||||
Vận tốc ô tô tại thời điểm bắt đầu phanh là: Vận tốc của chuyển động sau khi phanh là: Do Khi xe dừng hẳn tức là |
0.25 | ||||
Quãng đường
|
0.25 | ||||
| 4(0.5điểm) | Cho Z là số phức có mô đun bằng 2021 và W là số phức thỏa mãn  . Tìm mô đun số phức W.
. Tìm mô đun số phức W. |
||||
Từ giả thiết (*) suy ra
|
0.25 | ||||
|
0.25 |












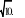

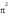
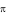

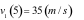 .
. .
.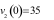

 .
.
 .
.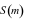 đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là:
đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là:
 .
.

