Bài 5: Phương trình mũ và phương trình lôgarit
Bài 2.30 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình mũ sau:
a) \({(0,75)^{2x - 3}} = {(1\frac{1}{3})^{5 - x}}\)
b) \({5^{{x^2} - 5x - 6}} = 1\)
c) \({(\frac{1}{7})^{{x^2} - 2x - 3}} = {7^{x + 1}}\)
d) \({32^{\frac{{x + 5}}{{x - 7}}}} = 0,{25.125^{\frac{{x + 17}}{{x - 3}}}}\)
Hướng dẫn giải
a) \({(\frac{3}{4})^{2x - 3}} = {(\frac{4}{3})^{5 - x}}\)
\( \Leftrightarrow {(\frac{3}{4})^{2x - 3}} = {(\frac{3}{4})^{x - 5}}\)
\(\Leftrightarrow 2x - 3 = x - 5 \Leftrightarrow x = - 2\)
b)
\(\begin{array}{l}
{5^{{x^2} - 5x - 6}} = {5^0} \Leftrightarrow {x^2} - 5x - 6 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 1\\
x = 6
\end{array} \right.
\end{array}\)
c)
\(\begin{array}{l}
{(\frac{1}{7})^{{x^2} - 2x - 3}} = {(\frac{1}{7})^{ - x - 1}} \Leftrightarrow {x^2} - 2x - 3 = - x - 1 \Leftrightarrow {x^2} - x - 2 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 1\\
x = 2
\end{array} \right.
\end{array}\)
d) \({2^{5.\frac{{x + 5}}{{x - 7}}}} = {2^{ - 2}}{.5^{3.\frac{{x + 17}}{{x - 3}}}} < = > {2^{\frac{{5x + 25}}{{x - 7}} + 2}} = {5^{\frac{{3x + 51}}{{x - 3}}}} < = > {2^{\frac{{7x + 11}}{{x - 7}}}} = {5^{\frac{{3x + 51}}{{x - 3}}}}\)
Lấy logarit cơ số 2 cả hai vế, ta được:
\(\frac{{7x + 11}}{{x - 7}} = \frac{{3x + 51}}{{x - 3}}{\log _2}5 < = > \left\{ {\begin{array}{*{20}{c}}
{7{x^2} - 10x - 33 = (3{x^2} + 30x - 357){{\log }_2}5}\\
{x \ne 7,x \ne 3}
\end{array}} \right.\)
\( < = > (7 - 3{\log _2}5){x^2} - 2(5 + 15{\log _2}5) - (33 - 357{\log _2}5) = 0\)
Ta có: \(\Delta ' = {(5 + 15{\log _2}5)^2} + (7 - 3{\log _2}5)(33 - 357{\log _2}5)\)
\( = 1296\log _2^25 - 2448{\log _2}5 + 256 > 0\)
Phương trình đã cho có hai nghiệm: \(x = \frac{{5 + 15{{\log }_2}5 \pm \sqrt {\Delta '} }}{{7 - 3{{\log }_2}5}}\) , đều thỏa mãn điều kiện
Bài 2.31 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình mũ sau:
a) \({2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {3.5^x}\)
b) \({5^{2x}} - {7^x} - {5^{2x}}.17 + {7^x}.17 = 0\)
c) \({4.9^x} + {12^x} - {3.16^x} = 0\)
d) \( - {8^x} + {2.4^x} + {2^x} - 2 = 0\)
Hướng dẫn giải
a) \({16.2^x} + {4.2^x} = {5.5^x} + {3.5^x}\)
\(\Leftrightarrow {20.2^x} = {8.5^x} \Leftrightarrow {(\frac{2}{5})^x} = {(\frac{2}{5})^1} \Leftrightarrow x = 1\)
b) \({16.7^x} - {16.5^{2x}} = 0\)
\( \Leftrightarrow {7^x} = {5^{2x}} \Leftrightarrow {(\frac{7}{{25}})^x} = {(\frac{7}{{25}})^0} \Leftrightarrow x = 0\)
c) Chia hai vế cho \({12^x}({12^x} > 0)\) , ta được:
\(4{(\frac{3}{4})^x} + 1 - 3{(\frac{4}{3})^x} = 0\)
Đặt \(t = {(\frac{3}{4})^x}\) (t > 0), ta có phương trình:
\(4t + 1 - \frac{3}{t} = 0 \Leftrightarrow 4{t^2} + t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{t = - 1(l)}\\
{t = \frac{3}{4}}
\end{array}} \right.\)
Do đó, \({(\frac{3}{4})^x} = {(\frac{3}{4})^1}\) . Vậy x = 1.
d) Đặt \(t = {2^x}(t > 0)\) , ta có phương trình:
\( - {t^3} + 2{t^2} + t - 2 = 0\)
\(\Leftrightarrow(t - 1)(t + 1)(2 - t) = 0 < = >\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{t = 1}\\
{t = - 1(l)}\\
{t = 2}
\end{array}} \right.\)
Do đó,
\(\left[ {\begin{array}{*{20}{c}}
{{2^x} = 1}\\
{{2^x} = 2}
\end{array}} \right.\)
Bài 2.32 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị:
a) \({2^{ - x}} = 3x + 10\)
b) \({(\frac{1}{3})^{ - x}} = - 2x + 5\)
c) \({(\frac{1}{3})^x} = x + 1\)
d) \({3^x} = 11 - x\)
Hướng dẫn giải
a) Vẽ đồ thị của hàm số: \(y = {2^{ - x}}\) và đường thẳng y = 3x +10 trên cùng một hệ trục tọa độ (H. 57) ta thấy chúng cắt nhau tại điểm có hoành độ x = -2. Thử lại, ta thấy x = -2 thỏa mãn phương trình đã cho.
Mặt khác, hàm số \(y = {2^{ - x}} = {(\frac{1}{2})^x}\) luôn nghịch biến, hàm số y = 3x + 10 luôn đồng biến.
Vậy x = -2 là nghiệm duy nhất.
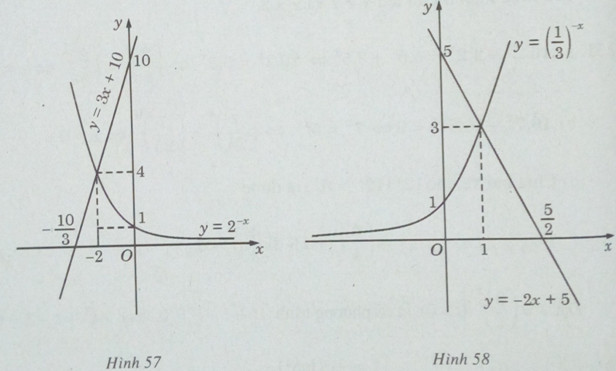
b) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^{ - x}}\) và đường thẳng y = -2x + 5 trên cùng một hệ trục tọa độ (H.58), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Thử lại, ta thấy x = 1 thỏa mãn phương trình đã cho.
Mặt khác, hàm số \(y = {(\frac{1}{3})^{ - x}} = {3^x}\) luôn đồng biến, hàm số y = -2x + 5 luôn nghịch biến.
Vậy x = 1 là nghiệm duy nhất.
c) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.59), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0. Thử lại, ta thấy x = 0 thỏa mãn phương trình đã cho. Mặt khác, \(y = {(\frac{1}{3})^x}\) là hàm số luôn nghịch biến, hàm số y = x +1 luôn đồng biến.
Vậy x = 0 là nghiệm duy nhất.
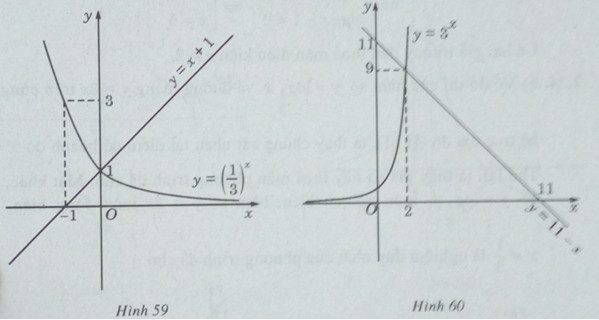
d) Vẽ đồ thị của hàm số và đường thẳng y = 11 – x trên cùng một hệ trục tọa độ (H.60), ta thấy chúng cắt nhau tại điểm có hoành độ x = 2. Thử lại, ta thấy x = 2 thỏa mãn phương trình đã cho. Mặt khác, \(y = {3^x}\) luôn đồng biến , y = 11 – x luôn nghịch biến . Vậy x = 2 là nghiệm duy nhất.
Bài 2.33 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình logarit sau:
a) \(\log x + \log {x^2} = \log 9x\)
b) \(\log {x^4} + \log 4x = 2 + \log {x^3}$\)
c) \({\log _4}{\rm{[}}(x + 2)(x + 3){\rm{]}} + {\log _4}\frac{{x - 2}}{{x + 3}} = 2\)
d) \({\log _{\sqrt 3 }}(x - 2){\log _5}x = 2{\log _3}(x - 2)\)
Hướng dẫn giải
a) Với điều kiện x > 0, ta có
\(\log x + 2\log x = \log 9 + \log x\)
\(\Leftrightarrow \log x = \log 3 \Leftrightarrow x = 3\)
b) Với điều kiện x > 0, ta có
\(4\log x + \log 4 + \log x = 2\log 10 + 3\log x\)
\( \Leftrightarrow \log x = \log 5 \Leftrightarrow x = 5\)
c) Ta có điều kiện của phương trình đã cho là:
\(\left\{ {\matrix{{(x + 2)(x + 3) > 0} \cr {{{x - 2} \over {x + 3}} > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{\left[ {\matrix{{x < - 3} \cr {x > - 2} \cr} } \right.} \cr {\left[ {\matrix{{x < - 3} \cr {x > 2} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x < - 3} \cr {x > 2} \cr} (1)} \right.\)
Khi đó, phương trình đã cho tương đương với:
\({\log _4}{\rm{[}}(x + 2)(x + 3)\frac{{x - 2}}{{x + 3}}{\rm{]}}\)
\(= {\log _4}16 \Leftrightarrow {x^2} - 4 = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 2\sqrt 5 }\\
{x = - 2\sqrt 5 }
\end{array}} \right.\)
Cả hai nghiệm trên đều thỏa mãn điều kiện (1).
d) Với điều kiện x > 2, ta có phương trình
\(2{\log _3}(x - 2)({\log _5}x - 1) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{{\log }_3}(x - 2) = 0}\\
{{{\log }_5}x - 1 = 0}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 3}\\
{x = 5}
\end{array}} \right.} \right.\)
Cả hai giá trị này đều thỏa mãn điều kiện x > 2.
Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình sau bằng phương pháp đồ thị:
a) \({\log _{\frac{1}{3}}}x = 3x\)
b) \({\log _3}x = - x + 11\)
c) \({\log _4}x = \frac{4}{x}\)
d) \({16^x} = {\log _{\frac{1}{2}}}x\)
Hướng dẫn giải
a) Vẽ đồ thị của hàm số \({\log _{\frac{1}{3}}}x = 3x\) và đường thẳng y = 3x trên cùng một hệ trục tọa độ (H.61), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\)
Thử lại, ta thấy giá trị này thỏa mãn phương trình đã cho. Mặt khác, hàm số \(y = {\log _{\frac{1}{3}}}x\) luôn nghịch biến, hàm số y = 3x luôn đồng biến. Vậy \(x = \frac{1}{3}\) là nghiệm duy nhất của phương trình đã cho.
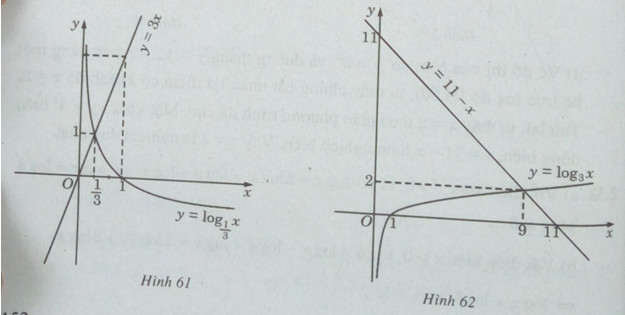
b) Vẽ đồ thị của hàm số \(y = {\log _3}x\) và đường thẳng y = - x + 11 trên cùng một hệ trục tọa độ (H.62) , ta thấy chúng cắt nhau tại điểm có hoành độ x = 9. Lập luận tương tự câu a), ta cũng có đây là nghiệm duy nhất của phương trình đã cho.
c) Vẽ đồ thị của các hàm số \(y = {\log _4}x\) và \(y = \frac{4}{x}\) trên cùng một hệ trục tọa độ (H.63), ta thấy chúng cắt nhau tại điểm có hoành độ x = 4. Ta cũng có hàm số \(y = {\log _3}x\) luôn đồng biến, hàm số \(y = \frac{4}{x}\) luôn nghịch biến trên \((0; + \infty )\) . Do đó, x = 4 là nghiệm duy nhất.
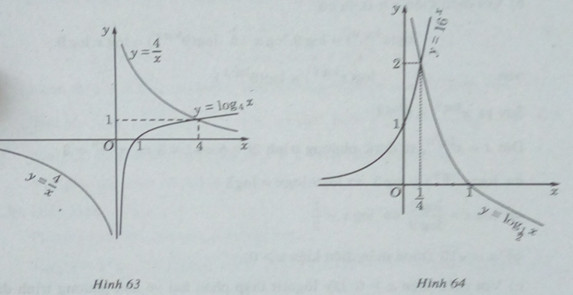
d) Vẽ đồ thị của các hàm số \(y = {16^x}\) và \(y = {\log _{\frac{1}{2}}}x\) trên cùng một hệ trục tọa độ (H.64), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{4}\) . Thử lại, ta thấy \(x = \frac{1}{4}\) thỏa mãn phương trình đã cho. Mặt khác, hàm số luôn đồng biến, hàm số luôn nghịch biến.
Vậy \(x = \frac{1}{4}\) là nghiệm duy nhất của phương trình.
Bài 2.35 trang 125 Sách bài tập (SBT) Giải tích 12
Giải các phương trình logarit :
a) \({\log _2}({2^x} + 1).{\log _2}({2^{x + 1}} + 2) = 2\)
b) \({x^{\log 9}} + {9^{\log x}} = 6\)
c) \({x^{3{{\log }^3}x - \frac{2}{3}\log x}} = 100\sqrt[3]{{10}}\)
d) \(1 + 2{\log _{x + 2}}5 = {\log _5}(x + 2)\)
Hướng dẫn giải
a) \({\log _2}({2^x} + 1).{\log _2}{\rm{[}}2({2^x} + 1){\rm{]}} = 2\)
\( \Leftrightarrow {\log _2}({2^x} + 1).{\rm{[}}1 + {\log _2}({2^x} + 1){\rm{]}} = 2\)
Đặt \(t = {\log _2}({2^x} + 1)\) , ta có phương trình
\(t(1 + t) = 2 ⇔ {t^2} + t – 2 = 0\)
\(\eqalign{& \Leftrightarrow \left[ {\matrix{{t = 1} \cr {t = - 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_2}({2^x} + 1) = 1} \cr {{{\log }_2}({2^x} + 1) = - 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{2^x} + 1 = 2} \cr {{2^x} + 1 = {1 \over 4}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{2^x} = 1} \cr {{2^x} = - {3 \over 4}(l)} \cr} } \right. \Leftrightarrow x = 0 \cr} \)
b) Với điều kiện x > 0, ta có: \(\log ({x^{\log 9}}) = \log ({9^{\log x}})\)
\(\log ({x^{\log 9}}) = \log 9.\log x\) và \(\log ({9^{\log x}}) = \log x.\log 9\)
Nên \(\log ({x^{\log 9}}) = \log ({9^{\log x}})\)
Suy ra:
\({t^4} + 14{t^2} - 32t + 17 = 0\)
\( \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \Leftrightarrow t = 1\) \({x^{\log 9}} = {9^{\log x}}\)
Đặt \(t = {x^{\log 9}}\) , ta được phương trình \(2t = 6 ⇔ t = 3 ⇔ {x^{\log 9}} = 3\)
\(\eqalign{
& \Leftrightarrow \log ({x^{\log 9}}) = \log 3 \cr
& \Leftrightarrow \log 9.\log x = \log 3 \cr
& \Leftrightarrow \log x = {{\log 3} \over {\log 9}} \cr
& \Leftrightarrow \log x = {1 \over 2} \cr}\)
\(\Leftrightarrow x = \sqrt {10} \) (thỏa mãn điều kiện x > 0)
c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:
\((3{\log ^3}x - \frac{2}{3}\log x).\log x = \frac{7}{3}\)
Đặt \(t = \log x\) , ta được phương trình \(3{t^4} - \frac{2}{3}{t^2} - \frac{7}{3} = 0\)
\(\eqalign{
& \Leftrightarrow 9{t^4} - 2{t^2} - 7 = 0 \Leftrightarrow \left[ \matrix{
{t^2} = 1 \hfill \cr
{t^2} = - {7 \over 9}\left( {loại} \right) \hfill \cr} \right.\left[ \matrix{
t = 1 \hfill \cr
t = - 1 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
\log x = 1 \hfill \cr
\log x = - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 10 \hfill \cr
x = {1 \over {10}} \hfill \cr} \right. \cr} \)
d) Đặt \(t = {\log _5}(x + 2)\) với điều kiện \(x + 2{\rm{ }} > 0,\,\,x + 2 \ne 1\) , ta có:
\(\eqalign{& 1 + {2 \over t} = t \Leftrightarrow {t^2} - t - 2 = 0,t \ne 0 \cr & \Leftrightarrow \left[ {\matrix{{t = - 1} \cr {t = 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_5}(x + 2) = - 1} \cr {{{\log }_5}(x + 2) = 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x + 2 = {1 \over 5}} \cr {x + 2 = 25} \cr} \Leftrightarrow \left[ {\matrix{{x = - {9 \over 5}} \cr {x = 23} \cr} } \right.} \right. \cr} \)
Bài 2.36 trang 126 Sách bài tập (SBT) Giải tích 12
Giải phương trình \({25^x} - {6.5^x} + 5 = 0\) (Đề thi tốt nghiệp THPT năm 2009)
Hướng dẫn giải
Đáp số: x = 0; x = 1.
Bài 2.37 trang 126 Sách bài tập (SBT) Giải tích 12
Giải phương trình: \({4^{2x + \sqrt {x + 2} }} + {2^{{x^3}}} = {4^{2 + \sqrt {x + 2} }} + {2^{{x^3} + 4x - 4}}\) (Đề thi đại học năm 2010, khối D)
Hướng dẫn giải
Điều kiện: \(x \ge - 2\)
Phương trình tương đương với:
\(({2^{4x}} - {2^4})({2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}}) = 0\) . Suy ra:
\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{2^{4x}} - {2^4} = 0}\\
{{2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}} = 0}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 1}\\
{2\sqrt {x + 2} = {x^3} - 4}
\end{array}} \right.\)
Nhận thấy \(x \ge \sqrt[3]{4}\)và phương trình có một nghiệm x = 2. Trên \({\rm{[}}\sqrt[3]{4}; + \infty )\) , hàm số \(f(x) = 2\sqrt {x + 2} - {x^3} + 4\) có đạo hàm \(f(x) = 2\sqrt {x + 2} - {x^3} + 4\) nên f(x) luôn nghịch biến. Suy ra x = 2 là nghiệm duy nhất.
Vậy phương trình có nghiệm x = 1; x = 2.
Bài 2.38 trang 126 Sách bài tập (SBT) Giải tích 12
Giải phương trình:
\(f(x) = 2\sqrt {x + 2} - {x^3} + 4{\log _2}(8 - {x^2}) + {\log _{\frac{1}{2}}}(\sqrt {1 + x} + \sqrt {1 - x} ) - 2 = 0\)
(Đề thi Đại học năm 2011, khối D)
Hướng dẫn giải
Điều kiện: \( - 1 \le x \le 1\)
Phương trình đã cho tương đương với:
\(\eqalign{
& {\log _2}(8 - {x^2}) = {\log _2}{\rm{[}}4(\sqrt {1 + x} + \sqrt {1 - x} ){\rm{]}} \cr
& \Leftrightarrow {(8 - {x^2})^2} = 16(2 + 2\sqrt {1 - {x^2}} ) \cr} \)
Đặt \(t = \sqrt {1 - {x^2}} \) ta được :
\(\eqalign{
& {t^4} + 14{t^2} - 32t + 17 = 0 \cr
& \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \cr
& \Leftrightarrow t = 1 \cr} \)
Suy ra x = 0. Vậy phương trình có nghiệm x = 0




