Bài 1: Hàm số lượng giác

Lý thuyết

Bài 1.1 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm tập xác định của các hàm số.

a) \(y = \cos {{2x} \over {x - 1}}\)     

b) \(y = \tan {x \over 3}\)     

c) \(y = \cot 2x\)    

d) \(y = \sin {1 \over {{x^2} - 1}}\)

Hướng dẫn giải

a) \(D = R\backslash \left\{ 1 \right\}\)     

b)  \(cos {x \over 3} \ne 0 \Leftrightarrow {x \over 3} \ne {\pi  \over 2} + k\pi  \Leftrightarrow x \ne {{3\pi } \over 2} + k3\pi ,k \in Z\)

Vậy \({\rm{ D  =  R\backslash }}\left\{ {{{3\pi } \over 2} + k3\pi ,{\rm{ }}k \in Z} \right\}\)

c) \(\sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi  \Leftrightarrow x \ne k{\pi  \over 2},k \in Z.\)    

 Vậy \({\rm{D  =  R\backslash }}\left\{ {k{\pi  \over 2},k \in Z} \right\}\)

d) \(D{\rm{  =  R\backslash }}\left\{ { - 1;1} \right\}\) 

Bài 1.2 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm tập xác định của các hàm số.

a) \(y = \sqrt {\cos x + 1} \)    

b) \(y = {3 \over {{{\sin }^2}x - {{\cos }^2}x}}\)   

c) \(y = {2 \over {\cos x - \cos 3x}}\)    

d) \(y = \tan x + \cot x\)

Hướng dẫn giải

a) \(\cos x + 1 \ge 0,\forall x \in R.{\rm{ }}\). Vậy D = R

b) \({\sin ^2}x - {\cos ^2}x =  - \cos 2x \ne 0 \Leftrightarrow 2x \ne {\pi  \over 2} + k\pi ,k \in Z \Leftrightarrow x \ne {\pi  \over 4} + k{\pi  \over 2},k \in Z.{\rm{ }}\)

Vậy \({\rm{D  =  R\backslash }}\left\{ {{\pi  \over 4} + k{\pi  \over 2},k \in Z} \right\}\)    

c) \(\cos x - \cos 3x =  - 2\sin 2x\sin ( - x) = 4{\sin ^2}x\cos x\)

\( \Rightarrow \cos x - \cos 3x \ne 0 \Leftrightarrow \sin x \ne 0\) và \(\cos x \ne 0\)

\( \Leftrightarrow x \ne k\pi \) và \(x \ne {\pi  \over 2} + k\pi ,k \in Z.\)

Vậy \(D = R\backslash \left\{ {{{k\pi } \over 2},k \in Z} \right\}\)

d) tan x và cos x có nghĩa khi sin x ≠ 0 và cos x ≠ 0

Vậy \(D = R\backslash \left\{ {{{k\pi } \over 2},k \in Z} \right\}\)

Bài 1.3 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số

a) \(y = 3 - 2\left| {\sin x} \right|\)    

b) \(y = \cos x + \cos \left( {x - {\pi  \over 3}} \right)\)    

c) \(y = {\cos ^2}x + 2\cos 2x\)   

d) \(y = \sqrt {5 - 2{{\cos }^2}x{{\sin }^2}x} \)    

Hướng dẫn giải

a) \(0 \le \left| {\sin x} \right| \le 1{\rm{nn}} - 2 \le  - 2\left| {\sin x} \right| \le 0\)

Vậy giá trị lớn nhất của y = 3 - 2|sin x| là 3, đạt được khi sin x = 0; giá trị nhỏ nhất của y là 1, đạt được khi sin x = ± 1

b) \(\cos x + \cos \left( {x - {\pi  \over 3}} \right)\)

\(= 2\cos \left( {x - {\pi  \over 6}} \right)\cos {\pi  \over 6}\)

\(= \sqrt 3 \cos \left( {x - {\pi  \over 6}} \right)\)

Vậy giá trị nhỏ nhất của y là -√3 đạt được chẳng hạn, tại \(x = {{7\pi } \over 6}\); giá trị lớn nhất của y là √3, đạt được chẳng hạn tại \(x = {\pi  \over 6}\)

c) Ta có:

\({\cos ^2}x + 2\cos 2x\)

\(= {{1 + \cos 2x} \over 2} + 2\cos 2x\)

\(= {{1 + 5\cos 2x} \over 2}\)

Vì -1 ≤ cos2x ≤ 1 nên giá trị lớn nhất của y là 3, đạt được khi x = 0, giá trị nhỏ nhất của y là -2, đạt được khi \(x = {\pi  \over 2}\)

d) \(5 - 2{\cos ^2}x{\sin ^2}x = 5 - {1 \over 2}{\sin ^2}2x\)

Vì \(0 \le {\sin ^2}2x \le 1\Rightarrow - {1 \over 2} \le  - {1 \over 2}{\sin ^2}2x \le 0{\rm{ }}\)

\(\Rightarrow {\rm{ }}{{3\sqrt 2 } \over 2} \le y \le \sqrt 5 \)

Suy ra giá trị lớn nhất của y = √5 tại \(x = k{\pi  \over 2}\), giá trị nhỏ nhất là \({{3\sqrt 2 } \over 2}\) tại \(x = {\pi  \over 4} + k{\pi  \over 2}\)

Bài 1.4 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Với những giá trị nào của x, ta có mỗi đẳng thức sau?

a) \({1 \over {\tan x}} = \cot x\)   

b) \({1 \over {1 + {{\tan }^2}x}} = {\cos ^2}x\)    

c) \({1 \over {{{\sin }^2}x}} = 1 + {\cot ^2}x\)    

d) \(\tan x + \cot x = {2 \over {\sin 2x}}\)  

Hướng dẫn giải

a) Đẳng thức xảy ra khi các biểu thức ở hai vế có nghĩa tức là sinx ≠ 0 và cosx ≠ 0. Vậy đẳng thức xảy ra khi \(x \ne k{\pi  \over 2}\) , k ∈ Z

b) Đẳng thức xảy ra khi cosx ≠ 0, tức là khi \(x \ne {\pi  \over 2} + k\pi\) k ∈ Z

c) Đẳng thức xảy ra khi sinx ≠ 0, tức là \(x \ne k\pi \), k ∈ Z

d) Đẳng thức xảy ra khi  sinx ≠ 0 và cosx ≠ 0, tức là \(x \ne k{\pi  \over 2}\), k ∈ Z

Bài 1.5 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Xác định tính chẵn lẻ của các hàm số 

a) \(y = {{\cos 2x} \over x}\)     

b) \(y = x - \sin x\)    

c) \(y = \sqrt {1 - \cos x} \)     

d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} - 2x} \right)\)    

Hướng dẫn giải

a) \(y = {{\cos 2x} \over x}\) là hàm số lẻ

b) \(y = x - \sin x\) là hàm số lẻ  

c) \(y = \sqrt {1 - \cos x} \) là hàm số chẵn

d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} - 2x} \right)\) là hàm số chẵn

Bài 1.6 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

a) Chứng minh rằng \(\cos 2\left( {x + k\pi } \right) = \cos 2x,k \in Z\) . Từ đó vẽ đồ thị hàm số y = cos 2x

b) Từ đồ thị hàm số y = cos 2x, hãy vẽ đồ thị hàm số y = |cos 2x|

Hướng dẫn giải

a) \(\cos 2(x + k\pi ) = \cos (2x + k2\pi ) = \cos 2x,k \in Z\). Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.

Đồ thị hàm số y = cos 2x

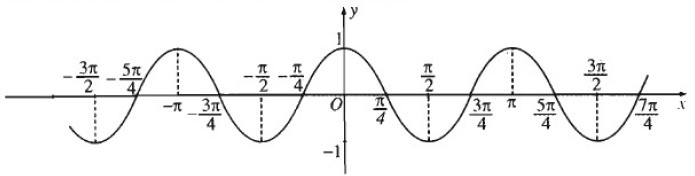
b) Đồ thị hàm số y = |cos 2x|

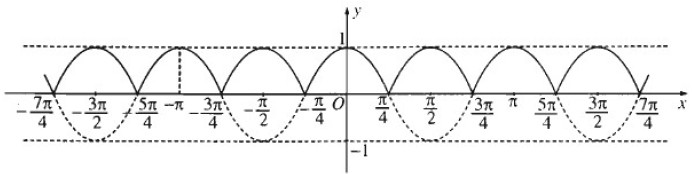
Bài 1.7 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Hãy vẽ đồ thị của các hàm số

a) y = 1 + sin x  

b) y = cos x - 1  

c) \(y = \sin \left( {x - {\pi  \over 3}} \right)\)    

d) \(y = \cos \left( {x + {\pi  \over 6}} \right)\)   

Hướng dẫn giải

a) Đồ thị hàm số y = 1 + sin x thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị.

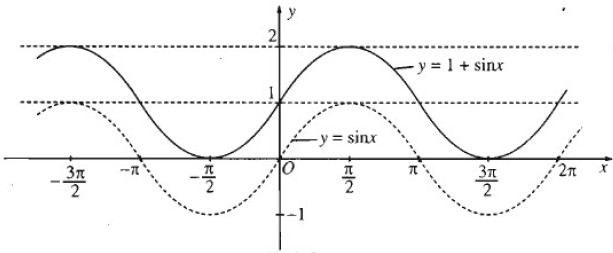
b) Đồ thị hàm số y = cos x - 1 thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục tung xuống phía dưới một đơn vị.

c) Đồ thị hàm số \(y = \sin \left( {x - {\pi  \over 3}} \right)\) thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi  \over 3}\)

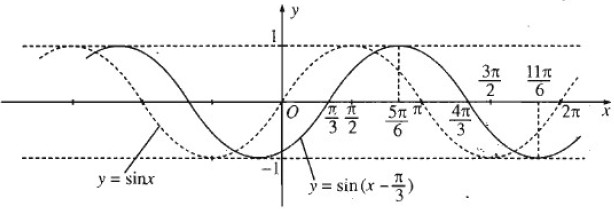
d) Đồ thị hàm số \(y = \cos \left( {x + {\pi  \over 6}} \right)\) thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi  \over 6}\)

Bài 1.8 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Hãy vẽ đồ thị của các hàm số 

a) \(y = \tan \left( {x + {\pi  \over 4}} \right)\)    

b) \(y = \cot \left( {x - {\pi  \over 6}} \right)\)   

Hướng dẫn giải

a) Đồ thị hàm số \(y = \tan \left( {x + {\pi  \over 4}} \right)\) thu được từ đồ thị hàm số y = tanx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi  \over 4}\).

b) Đồ thị hàm số \(y = \cot \left( {x - {\pi  \over 6}} \right)\) thu được từ đồ thị hàm số y = cotx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi  \over 6}\)