Ôn tập chương III
Bài 3.37 trang 160 Sách bài tập (SBT) Toán Hình học 10
Cho ba điểm A(2;1), B(0;5), C(-1;-10).
a) Tìm tọa độ trọng tâm G, trực tâm H và tâm I đường tròn ngoại tiếp tam giác ABC.
b) Chứng minh I, G, H thẳng hàng.
c) Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải
a) + Trọng tâm \(G\left( { - 1; - {4 \over 3}} \right)\)
+ Tọa độ trực tâm H(x;y)
\(\eqalign{
& \overrightarrow {AH} (x - 2;y - 1) \cr
& \Rightarrow \overrightarrow {AH} .\overrightarrow {BC} = (x - 2).( - 5) + (y - 1).( - 15) \cr} \)
\(\eqalign{
& \overrightarrow {BH} = (x;y - 5) \cr
& \Rightarrow \overrightarrow {BH} .\overrightarrow {CA} = x.( - 7) + (y - 5).( - 11) \cr} \)
Do là trực tâm
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
\overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BH} .\overrightarrow {CA} = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
(x - 2).( - 5) + (y - 1).( - 15) = 0 \hfill \cr
x.( - 7) + (y - 5).( - 11) = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x = 11 \hfill \cr
y = - 2 \hfill \cr} \right. \cr} \)
+ Tọa độ tâm đường tròn ngoại tiếp I(x;y)
\(AI_{}^2 = (x - 2)_{}^2 + (y - 1)_{}^2\)
\(BI_{}^2 = x_{}^2 + (y - 5)_{}^2\)
\(CI_{}^2 = (x + 5)_{}^2 + (y + 10)_{}^2\)
Ta có:
\(\eqalign{
& AI_{}^2 = BI_{}^2 = CI_{}^2 \Leftrightarrow \left\{ \matrix{
AI_{}^2 = BI_{}^2 \hfill \cr
BI_{}^2 = CI_{}^2 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
(x - 2)_{}^2 + (y - 1)_{}^2 = x_{}^2 + (y - 5)_{}^2 \hfill \cr
x_{}^2 + (y - 5)_{}^2 = (x + 5)_{}^2 + (y + 10)_{}^2 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x = - 7 \hfill \cr
y = - 1 \hfill \cr} \right. \cr} \)
b) Ta có: \(\overrightarrow {IH} (18; - 1)\), \(\overrightarrow {IG} \left( {6; - {1 \over 3}} \right)\)
\( \Rightarrow \overrightarrow {IH} = 3\overrightarrow {IG} \) suy ra I,G,H thẳng hàng.
c) Ta có:
\(R = IA = \sqrt {( - 7 - 2)_{}^2 + ( - 1 - 1)_{}^2} = \sqrt {85} \)
Phương trình đường tròn ngoại tiếp tam giác ABC là: \((x + 7)_{}^2 + (y + 1)_{}^2 = 85\)
Bài 3.38 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho đường thẳng \(\Delta \) có phương trình tham số
\(\left\{ \matrix{
x = 2 - 3t \hfill \cr
y = t. \hfill \cr} \right.\)
a) Hai điểm A(-7;3) và B(2;1) có nằm trên \(\Delta \) không ?
b) Tìm tọa độ giao điểm của \(\Delta \) với hai trục Ox và Oy.
c) Tìm trên \(\Delta \) điểm M sao cho đoạn BM ngắn nhất.
Hướng dẫn giải
a) Thay tọa độ A, B vào phương trình tham số của \(\Delta \) ta có: \(A \in \Delta ,B \notin \Delta \)
b) Trục Oy : x = 0 thay vào phương trình tham số
\( \Rightarrow \left\{ \matrix{
0 = 2 - 3t \hfill \cr
y = t \hfill \cr} \right. \Leftrightarrow y = {2 \over 3}\)
Vậy giao điểm của \(\Delta \) và Oy là \(\left( {0;{2 \over 3}} \right)\).
Ox : y = 0 thay vào phương trình tham số
\( \Rightarrow \left\{ \matrix{
x = 2 - 3t \hfill \cr
0 = t \hfill \cr} \right. \Leftrightarrow x = 2\)
Vậy giao điểm của \(\Delta \) và Ox là (0;2).
c) Vì $\(M \in \Delta \) nên tọa độ M có dạng \(\left( {2 - 3t;t} \right)\)
\(\overrightarrow {BM} = \left( { - 3t;t - 1} \right)\)
\({\overrightarrow u _\Delta } = ( - 3;1).\)
Ta có : BM ngắn nhất
\( \Leftrightarrow BM \bot {\overrightarrow u _\Delta } \Leftrightarrow 9t + t - 1 = 0 \Leftrightarrow t = {1 \over {10}}.\)
Vậy điểm M thỏa mãn đề bài có tọa độ là \(\left( {{{17} \over {10}};{1 \over {10}}} \right).\)
Bài 3.39 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho hình chữ nhật ABCD. Biết A(3;0), B(-3;3) và phương trình đường thẳng chứa cạnh CD : x + 2y - 8 = 0. Tìm phương trình các đường thẳng chứa các cạnh còn lại.
Hướng dẫn giải
AB:x + 2y - 3 = 0;
AD:2x - y - 6 = 0;
BC:2x - y + 9 = 0.
Bài 3.40 trang 161 Sách bài tập (SBT) Toán Hình học 10
Trong mặt phẳng Oxy cho đường thẳng \(\Delta :x - y + 2 = 0\) và điểm A(2;0).
a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng .
b) Tìm điểm M trên \(\Delta \) sao cho độ dài đường gấp khúc OMA ngắn nhất.
Hướng dẫn giải
(h.3.11)
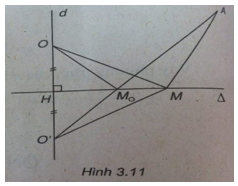
Ta có:
\(\Delta \left( O \right) = 2 > 0\)
\(\Delta \left( A \right) = 2 + 2 > 0\)
Vậy A và O nằm về cùng một phía đối với \(\Delta \)
b) Gọi O' là điểm đối xứng của O qua \(\Delta \), ta có:
\(OM + MA = O'M + MA \ge O'A\)
Ta có : OM + MA ngắn nhất
\( \Leftrightarrow O',M,A\) thẳng hàng
Xét đường thẳng d đi qua O và vuông góc với \(\Delta \) . Phương trình của d là:
x + y = 0
d cắt \(\Delta \) tại H(-1;1).
H là trung điểm của OO' suy ra \(O'\left( { - 2;2} \right)\)
Phương trình đường thẳng O'A là: x + 2y - 2 = 0
Giải hệ phương trình
\(\left\{ \matrix{
x + 2y = 2 \hfill \cr
x - y = - 2 \hfill \cr} \right.\)
ta được \(M = \left( { - {2 \over 3};{4 \over 3}} \right).\)
Bài 3.41 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho ba điểm A(3;5), B(2;3), C(6;2).
a) Viết phương trình đường tròn (C) ngoại tiếp tam giác ABC.
b) Hãy xác định tọa độ của tâm và bán kính của (C).
Hướng dẫn giải
a) (C) : \({x^2} + {y^2} - {{25} \over 3}x - {{19} \over 3}y + {{68} \over 3} = 0.\)
b) (C) có tâm \(I\left( {{{25} \over 6};{9 \over 6}} \right)\) và bán kính \(R = \sqrt {{{85} \over {18}}} .\)
Bài 3.42 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho phương trình \({x^2} + {y^2} - 2mx - 4(m - 2)y + 6 - m = 0\,(1)\)
a) Tìm điều kiện của m để (1) là phương tình của đường tròn, ta kí hiệu là (Cm).
b) Tìm tập hợp các tâm của (Cm) khi m thay đổi.
Hướng dẫn giải
a) (1) là phương trình của đường tròn khi và chỉ khi:
\(\eqalign{
& {a^2} + {b^2} - c > 0 \cr
& \Leftrightarrow {m^2} + 4{(m - 2)^2} - 6 + m > 0 \cr} \)
\( \Leftrightarrow 5m^2 - 15m + 10 > 0 \Leftrightarrow \left[ \matrix{
m < 1 \hfill \cr
m > 2. \hfill \cr} \right.\)
b) (Cm) có tâm I(x;y) thỏa mãn:
\(\left\{ \matrix{
x = m \hfill \cr
y = 2(m - 2) \hfill \cr} \right. \Leftrightarrow y = 2x - 4.\)
Vậy tập hợp các tâm của (C m) là một phần của đường thẳng \(\Delta :y = 2x - 4\) thỏa mãn điều kiện giới hạn ở câu a.
Bài 3.43 trang 161 Sách bài tập (SBT) Toán Hình học 10
Lập phương trình chính tắc của elip (E) trong mỗi trường hợp sau:
a) Một đỉnh là (0;-2) và một tiêu điểm là (-1;0) ;
b) Tiêu cự bằng 6, tỉ số \({c \over a}\) bằng \({3 \over 5}\).
Hướng dẫn giải
a) \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\);
b) \((E):{{{x^2}} \over {25}} + {{{y^2}} \over {16}} = 1.\)
Bài 3.44 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho elip (E) : \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\) và đường thẳng \(\Delta \) thay đổi có phương trình tổng quát Ax + By + C = 0 luôn thỏa mãn \(25{A^2} + 9{B^2} = {C^2}\). Tính tích khoảng cách từ hai tiêu điểm \({F_1}\), \({F_2}\) của (E) đến đường thẳng \(\Delta \)
Hướng dẫn giải
\((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\)
Ta có:
\({a^2} = 25,{b^2} = 9 \Rightarrow {c^2} = {a^2} - {b^2} = 16\)
\( \Rightarrow c = 4.\)
Vậy (E) có hai tiêu điểm là \({F_1}\left( { - 4;0} \right)\) và \({F_2}\left( {4;0} \right)\). Ta có :
\({d_1} = d({F_1},\Delta ) = {{\left| { - 4A + C} \right|} \over {\sqrt {{A^2} + {B^2}} }}\)
\({d_2} = d({F_2},\Delta ) = {{\left| {4A + C} \right|} \over {\sqrt {{A^2} + {B^2}} }}\)
Suy ra:
\({d_1}{d_2} = {{\left| {{C^2} - 16{A^2}} \right|} \over {{A^2} + {B^2}}}.\,\,\,(1)\)
Thay \({C^2} = 25{A^2} + 9{B^2}\) vào (1) ta được :
\(\eqalign{
& {d_1}{d_2} = {{\left| {25{A^2} + 9{B^2} - 16{A^2}} \right|} \over {{A^2} + {B^2}}} \cr
& = {{9({A^2} + {B^2})} \over {{A^2} + {B^2}}} \cr} \)
Vậy \({d_1}{d_2} = 9.\)
Bài 3.45 trang 161 Sách bài tập (SBT) Toán Hình học 10
Cho elip (E): \({x^2} + 4{y^2} = 16\).
a) Xác định tọa độ các tiêu điểm và các đỉnh của elip (E).
b) Viết phương trình đường thẳng \(\Delta \) đi qua điểm \(M\left( {1;{1 \over 2}} \right)\) và vectơ pháp tuyến \(\overrightarrow n = (1;2)\)
c) Tìm tọa độ giao điểm A và B của đường thẳng \(\Delta \) và elip (E). Chứng minh MA = MB.
Hướng dẫn giải
a) \(\eqalign{
& (E):{x^2} + 4{y^2} = 16 \cr
& \Leftrightarrow {{{x^2}} \over {16}} + {{{y^2}} \over 4} = 1. \cr} \)
Ta có:
\(\eqalign{
& {a^2} = 16,{b^2} = 4 \cr
& \Rightarrow {c^2} = {a^2} - {b^2} = 12 \cr} \)
\( \Rightarrow c = 2\sqrt 3 .\)
Vậy (E) có hai tiêu điểm: \({F_1}\left( { - 2\sqrt 3 ;0} \right)\) và \({F_2}\left( {2\sqrt 3 ;0} \right)\)
và các đỉnh \({A_1}\left( { - 4;0} \right)\), \({A_2}\left( {4;0} \right)\), \({B_1}\left( {0; - 2} \right)\), \({B_2}\left( {0;2} \right)\)
b) Phương trình \(\Delta \) có dạng :
\(1.(x - 1) + 2.(y - {1 \over 2}) = 0\)
hay \(x + 2y - 2 = 0\)
c) Tọa độ của giao điểm của \(\Delta \) và (E) là nghiệm của hệ :
\(\left\{ \matrix{
{x^2} + 4{y^2} = 16\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \cr
x = 2 - 2y.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \hfill \cr} \right.\)
Thay (2) vào (1) ta được :
\({\left( {2 - y} \right)^2} + 4{y^2} = 16\)
\( \Leftrightarrow {(1 - y)^2} + {y^2} = 4\)
\( \Leftrightarrow 2{y^2} - 2y - 3 = 0.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\)
Phương trình (3) có hai nghiệm \({y_A}\), \({y_B}\) thỏa mãn
\({{{y_A} + {y_B}} \over 2} = {2 \over 4} = {1 \over 2} = {y_M}.\)
Vậy MA = MB.
Ta có: \({y_A} = {{1 - \sqrt 7 } \over 2}\), \({y_B} = {{1 + \sqrt 7 } \over 2}\)
\({x_A} = 1 + \sqrt 7 \), \({x_B} = 1 - \sqrt 7 \)
Vậy A có tọa độ là \(\left( {1 + \sqrt 7 ;{{1 - \sqrt 7 } \over 2}} \right)\), B có tọa độ là \(\left( {1 - \sqrt 7 ;{{1 + \sqrt 7 } \over 2}} \right).\)




