§2. Tổng và hiệu của hai vectơ

Lý thuyết

Bài 1.8 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho năm điểm A, B, C, D và E. Hãy xác định tổng \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DE} \)

Hướng dẫn giải

\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {DE} \cr 
& = \overrightarrow {AD} + \overrightarrow {DE} = \overrightarrow {AE} \cr} \)

Bài 1.9 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho bốn điểm A, B, C và D. Chứng minh \(\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD} \)

Hướng dẫn giải

\(\eqalign{
& \overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {BD} \cr 
& \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {CD} \cr 
& \Leftrightarrow \overrightarrow {AD} = \overrightarrow {AD} \cr} \)

Như vậy hệ thức cần chứng minh tương đương với đẳng thức đúng.

Bài 1.10 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) sao cho \(\overrightarrow a  + \overrightarrow b  = \overrightarrow 0 \)

a)Dựng \(\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {OB}  = \overrightarrow b \). Chứng minh O là trung điểm của AB.

b)Dựng \(\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {AB}  = \overrightarrow b \). Chứng minh O=B

Hướng dẫn giải

a) \(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow 0  =  > \overrightarrow {OB}  =  - \overrightarrow {OA}  =  > OB = OA\) ba điểm A, O, B thẳng hàng và điểm O ở giữa A và B. Suy ra O là trung điểm của AB.

b) \(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow 0  =  > \overrightarrow {OB}  = \overrightarrow 0  =  > B \equiv O\)

Bài 1.11 trang 23 Sách bài tập (SBT) Toán Hình học 10

Gọi O là tâm của tam giác đều ABC. Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \)

Hướng dẫn giải

Trong tam giác đều ABC, tâm O của đường tròn ngoại tiếp cũng là trọng tâm của tam giác. Vậy \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \)

Bài 1.12 trang 23 Sách bài tập (SBT) Toán Hình học 10

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0\)

Hướng dẫn giải

\(\eqalign{
& \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) \cr 
& = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \cr} \)

Bài 1.14 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:

a) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {BA} \)

b) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {AB} \)

c) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 \)

Hướng dẫn giải

a) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {BA}  \Leftrightarrow \overrightarrow {BA}  = \overrightarrow {BA} \). Vậy mọi điểm M đều thỏa mãn hệ thức a).

b) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {AB}  \Leftrightarrow \overrightarrow {BA}  = \overrightarrow {AB}  \Leftrightarrow A \equiv B\), vô lí. Vậy không có điểm M nào thỏa mãn hệ thức b).

c) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {MA}  =  - \overrightarrow {MB} \). Vậy M là trung điểm của đoạn thẳng AB.

Bài 1.15 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Chứng minh rằng nếu \(\left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right|\) thì tam giác ACB là tam giác vuông cân tại C.

Hướng dẫn giải

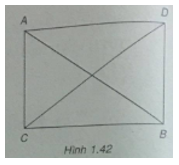
Vẽ hình bình hành CADB. 

Ta có \(\overrightarrow {CA}  + \overrightarrow {CB}  = \overrightarrow {CD} \), do đó \(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right| = CD\)

Vì \(\overrightarrow {CA}  - \overrightarrow {CB}  = \overrightarrow {BA} \), do đó \(\left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right| = BA\)

Từ \(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right|\) suy ra CD = AB (h.1.42)

Vậy tứ giác CADB là hình chữ nhật. Ta có tam giác ACB vuông tại C.

Bài 1.16 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho ngũ giác ABCDE. Chứng minh \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  = \overrightarrow {AE}  - \overrightarrow {DE} \)

Hướng dẫn giải

\(\eqalign{
& \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AE} - \overrightarrow {DE} \cr 
& \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AE} + \overrightarrow {ED} \cr 
& \Leftrightarrow \overrightarrow {AD} = \overrightarrow {AD} \cr} \)

Bài 1.17 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho ba điểm O, A, B không thẳng hàng. Với điều kiện nào thì vec tơ \(\overrightarrow {OA}  + \overrightarrow {OB} \) nằm trên đường phân giác của góc \(\widehat {AOB}\)?

Hướng dẫn giải

\(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC} \) trong đó OACB là hình bình hành. OC là phân giác góc \(\widehat {AOB}\) khi và chỉ khi OACB là hình thoi, tức là OA = OB.