Bài 4 (SGK trang 50)

Lý thuyết

Câu hỏi

Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC và tiếp xúc với ba cạnh ABm BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều ?

Hướng dẫn giải

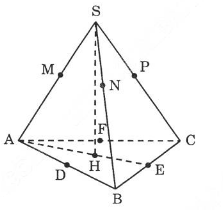
Gọi M, N, P theo thứ tự là các tiếp điểm của mặt cầu với các cạnh SA, SB, SC; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, CA, các điểm D, E, F đồng thời cũng là tiếp điểm của mặt cầu với các cạnh AB, BC, CA.

Ta có: AD = AF $=>\; AB\; =\; AC$

BD = BE$=>$ BC = AB

$=>$ AB = BC = CA

$=>$ \(\Delta ABC\) là tam giác đều (1)

Ta lại có AM = AD; BN = BD = AD

và SM = SN = SP

$=>$ SM + AM = SN + NB

$=>$ SA = SB

Chứng minh tương tự ta có: SA = SB = SC.

Gọi H là chân đường cao của hình chóp kẻ từ đỉnh S, ta có:

\(\Delta SHA=\Delta SHB=\Delta SHC\) =>$\Rightarrow$ HA = HB = HC

$=>$ H là tâm của tam giác đều ABC (2)

Từ (1) và (2) suy ra hình chóp S.ABC là hình chóp tam giác đều.

Update: 26 tháng 12 2018 lúc 14:56:56

Các câu hỏi cùng bài học

• Bài 5 (SGK trang 50)
• Bài 7 (SGK trang 50)
• Bài 2 (SGK trang 50)
• Bài 1 (SGK trang 50)
• Bài 3 (SGK trang 50)
• Bài 4 (SGK trang 50)
• Bài 6 (SGK trang 50)