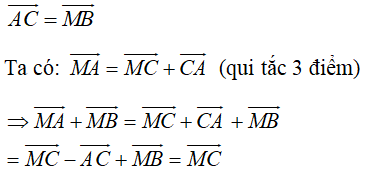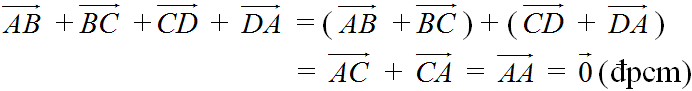§2. Tổng và hiệu của hai vectơ

Lý thuyết

Bài 1 (SGK trang 12)

Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho \(AM>MB\). Vẽ các vectơ \(\overrightarrow{MA}+\overrightarrow{MB}\) và \(\overrightarrow{MA}-\overrightarrow{MB}\) ? 

Hướng dẫn giải

Bài 2 (SGK trang 12)

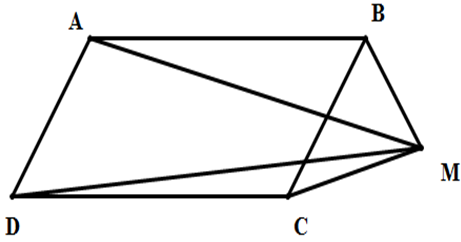
Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng \(\overrightarrow{MA+}\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\) ?

Hướng dẫn giải

Bài 3 (SGK trang 12)

Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có :

a) \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{O}\)

b) \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)

Hướng dẫn giải

Bài 4 (SGK trang 12)

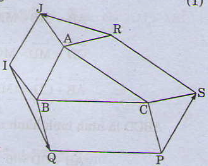
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{O}\) ?

Hướng dẫn giải

Ta xét tổng:

+ + + + + = = (1)

Mặt khác, ta có ABIJ, BCPQ và CARS là các hình bình hành nên:

=

=

=

=> ++ = + + = = (2)

Từ (1) và (2) suy ra : + + = (dpcm)

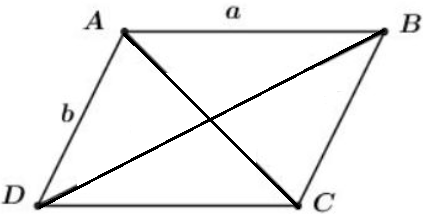
Bài 5 (SGK trang 12)

Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow{AB}+\overrightarrow{BC}\) và \(\overrightarrow{AB}-\overrightarrow{BC}\) ?

Hướng dẫn giải

Bài 6 (SGK trang 12)

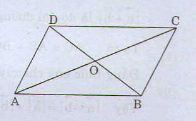
Cho hình bình hành ABCD có tâm O. Chứng minh rằng :

a) \(\overrightarrow{CO}-\overrightarrow{OB}=\overrightarrow{BA}\)

b) \(\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{DB}\)

c) \(\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{OD}-\overrightarrow{OC}\)

d) \(\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{0}\)

Hướng dẫn giải

a) Ta có, theo quy tắc ba điểm của phép trừ:

= - (1)

Mặt khác, = (2)

Từ (1) và (2) suy ra:

= - .

b) Ta có : = - (1)

= (2)

Từ (1) và (2) cho ta:

= - .

c) Ta có :

- = (1)

- = (2)

= (3)

Từ (1), (2), (3) suy ra đpcm.

d) - + = ( - ) + = + = + ( vì = ) =

Bài 7 (SGK trang 12)

Cho \(\overrightarrow{a},\overrightarrow{b}\) là hai vectơ khác \(\overrightarrow{0}\). Khi nào có đẳng thức :

a) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\)

b) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}-\overrightarrow{b}\right|\)

Hướng dẫn giải

Bài 8 (SGK trang 12)

Cho \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=0\). So sánh độ dài, phương và hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) ?

Hướng dẫn giải

Từ = 0, ta có + = 0 => = -

Điều này chứng tỏ hai vectơ có cùng độ dài = , cùng phương và ngược hướng

Bài 9 (SGK trang 12)

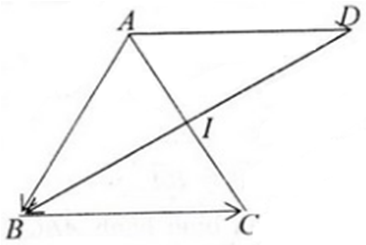
Chứng minh rằng \(\overrightarrow{AB}=\overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau ?

Hướng dẫn giải

Nếu \(\overrightarrow{AB}=\overrightarrow{CD}\) thì AD và BC có trung điểm trùng nhau. Gọi I là trung điểm của AD ta chứng minh I cũng là trung điểm của BC.

Theo quy tắc của ba điểm của tổng, ta có

\(\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB};\overrightarrow{CD}=\overrightarrow{CI}+\overrightarrow{ID}\)

Vì \(\overrightarrow{AB}=\overrightarrow{CD}\) nên \(\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\)

\(\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)

\(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{CI}+\overrightarrow{BI}\left(1\right)\)

Vì I là trung điểm của AD nên \(\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\left(2\right)\)

Từ (1) và (2) suy ra \(\overrightarrow{CI}+\overrightarrow{BI}=\overrightarrow{0}\left(3\right)\)

Từ (3) ta có chung điểm I, ta chứng minh \(\overrightarrow{AB}=\overrightarrow{CD}\)

I là trung điểm AD \(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{0}\)

I là trung điểm BC \(\Rightarrow\overrightarrow{CI}+\overrightarrow{BI}=0\Rightarrow\overrightarrow{CI}-\overrightarrow{IB}=\overrightarrow{0}\)

Suy ra \(\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)

\(\Rightarrow\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\)

Bài 10 (SGK trang 12)

Cho ba lực \(\overrightarrow{F_1}=\overrightarrow{MA};\overrightarrow{F_2}=\overrightarrow{MB};\overrightarrow{F_3}=\overrightarrow{MC}\) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow{F_1},\overrightarrow{F_2}\) đều là 100N và \(\widehat{AMB}=60^0\). Tìm cường độ và hướng của lực \(\overrightarrow{F_3}\) ?

Hướng dẫn giải

\(\left|\overrightarrow{F_3}\right|=100\sqrt{3}\) và \(\overrightarrow{F_3}\) ngược hướng với hướng \(\overrightarrow{ME}\) với E là đỉnh thứ tư của hình bình hành MACB

Bài 1.9 (STB trang 23)

Cho bốn điểm A, B, C và D. Chứng minh \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\) ?

 

Hướng dẫn giải

Giả sử \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\)
\(\Leftrightarrow\overrightarrow{AB}+\overrightarrow{DC}-\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}-\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AD}+\overrightarrow{DA}=\overrightarrow{0}\).
Vậy điều giả sử đúng. Ta có điều phải chứng minh.

Bài 1.10 (STB trang 23)

Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) sao cho \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\)

a) Dựng \(\overrightarrow{OA}=\overrightarrow{a};\overrightarrow{OB}=\overrightarrow{b}\). Chứng minh O là trung điểm của AB

b) Dựng \(\overrightarrow{OA}=\overrightarrow{a};\overrightarrow{AB}=\overrightarrow{b}\). Chứng minh \(O\equiv B\)

Hướng dẫn giải

Do \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đối nhau.
a)
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên O là trung điểm của AB.
b) \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên \(O\equiv B\).

Bài 1.11 (STB trang 23)

Gọi O là tâm của tam giác đều ABC. Chứng minh rằng : \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\) ?

 

Hướng dẫn giải

trong tam giác đều ABC , tâm O của đường tròn ngoại tiếp cũng là trọng tâm của tam giác .

vậy \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\) (ĐPCM)

Bài 1.12 (STB trang 23)

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{O}\) ?

Hướng dẫn giải

\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\left(\overrightarrow{OB}+\overrightarrow{OC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}\)(Theo tính chất hình bình hành).
\(=\overrightarrow{0}\) .

Bài 1.13 (STB trang 23)

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC; BE cắt AM tại N. Chứng minh \(\overrightarrow{NA}\) và \(\overrightarrow{NM}\) là hai vectơ đối nhau.

Hướng dẫn giải

Kẻ đoạn thẳng MF.
Do AE = EF nên E là trung điểm AF.
Trong tam giác ABC có AM là đường trung tuyến nên M là trung điểm của BC.
Vì vậy: MF là đường trung bình của tam giác BEC.
Suy ra: MF//BE.
Trong tam giác AMF có E là trung điểm của AF, BE//MF nên BE đi qua trung điểm của AM hay N là trung điểm của AM.
Vì vậy \(\overrightarrow{NA}\) và \(\overrightarrow{NM}\) là hai véc tơ đối nhau.

Bài 1.14 (STB trang 23)

Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau :

a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\)

b) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\)

c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\)

Hướng dẫn giải

a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
Vậy bất kì điểm M nào nằm trên mặt phẳng cũng thỏa mãn:
\(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\).
b) Do \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\) nên không tồn tại điểm M thỏa mãn: \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\).
c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) nên M là trung điểm của AB.

Bài 1.15 (STB trang 23)

Cho tam giác ABC. Chứng minh rằng nếu \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CA}-\overrightarrow{CB}\right|\) thì tam giác ABC là tam giác vuông tại C ?

Hướng dẫn giải

Dựng hình hình hành CADB.

Theo quy tắc hình bình hành: \(\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CD}\).
Vì vậy \(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=\left|\overrightarrow{CD}\right|=CD\);
Mặt khác \(\left|\overrightarrow{CA}-\overrightarrow{CB}\right|=\left|\overrightarrow{CA}+\overrightarrow{BC}\right|=\left|\overrightarrow{BA}\right|=BA\).
Suy ra: \(CD=AB\).
Hình bình hành CADB có hai đường chéo bằng nhau (\(CD=AB\) )nên hình bình hành CADB là hình chữ nhật.

Bài 1.16 (STB trang 23)

Cho ngũ giác ABCDE. Chứng minh \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AE}-\overrightarrow{DE}\) ?

Hướng dẫn giải

VT = \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\).
VP = \(\overrightarrow{AE}-\overrightarrow{DE}=\overrightarrow{AE}+\overrightarrow{ED}=\overrightarrow{AD}\).
VT = VP (đpcm).

Bài 1.17 (STB trang 23)

Cho 3 điểm O, A, B không thẳng hàng. Với điều kiện nào thì vectơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác của góc \(\widehat{AOB}\) ?

Hướng dẫn giải

a) Giả sử véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) .
Dựng hình bình hành OABD.

Theo quy tắc hình bình hành: \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\).
Theo giả thiết thì OD là tia phân giác góc \(\widehat{AOB}\).
Vì vậy hình bình hành OABD là hình thoi.
Suy ra OA = OB.
- Giả sử OA = OB.
Khi đó hình bình hành OABD có OA = OB nên tứ giác OABD là hình thoi.
Kết luận: Điều kiện cần và đủ để véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) là OA = OB.

Bài 1.18 (STB trang 23)

Cho hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) có điểm đặt O vào tạo với nhau góc \(60^0\). Tìm cường độ tổng lực của hai lực ấy biết rằng cường  độ của hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) đều là 100N

Hướng dẫn giải

Đặt \(\overrightarrow{F_1}=\overrightarrow{OA};\overrightarrow{F_2}=\overrightarrow{OB}\) ; \(\left|\overrightarrow{OA}\right|=100;\left|\overrightarrow{OB}\right|=100\).

Dựng hình bình hành OBDA.
Theo quy tắc hình bình hành \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\).
Do OA = OB = 100 nên tứ giác OBDA là hình thoi.
Vì vậy \(OD\perp AB\) và \(OD=2OK\).
Áp dụng định lý Pi-ta-go \(OK=\sqrt{OA^2-AK^2}=\sqrt{100^2-50^2}=50\sqrt{3}\).
\(OD=2OK=2.50\sqrt{3}=100\sqrt{3}\).
Vì vậy \(\left|\overrightarrow{OD}\right|=100\sqrt{3}\).
Từ đó duy ra: \(\left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|=100\sqrt{3}\).
Vì vậy cường độ tổng lực của \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) là \(100\sqrt{3}N\).

Bài 1.19 (STB trang 23)

Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng :

a) \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)

b) \(\overrightarrow{BD}=\overrightarrow{ME}+\overrightarrow{FN}\)

Hướng dẫn giải

a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).