§1. Hàm số

Lý thuyết

Bài 1 (SGK trang 38)

Tìm tập xác định của các hàm số :

a. \(y=\dfrac{3x-2}{2x+1}\)

b. \(y=\dfrac{x-1}{x^2+2x-3}\)

c. \(y=\sqrt{2x+1}-\sqrt{3-x}\)

 

Hướng dẫn giải

a) Công thức có nghĩa với x ∈ R sao cho 2x + 1 ≠ 0.

Vậy tập xác định của hàm số là:

D = { x ∈ R/2x + 1 ≠ 0} =

b) Tương tự như câu a), tập xác định của hàm số đã cho là:

D = { x ∈ R/x² + 2x - 3 ≠ 0}

x² + 2x – 3 = 0 ⇔ x = -3 hoặc x = 1

Vậy D = R {- 3; 1}.

c) có nghĩa với x ∈ R sao cho 2x + 1 ≥ 0

có nghĩa với x ∈ R sao cho 3 - x ≥ 0

Vậy tập xác định của hàm số là:

D = D₁ ∩ D₂, trong đó:

D₁ = {x ∈ R/2x + 1 ≥ 0} =

D₂ = {x ∈ R/3 - x ≥ 0} =

Bài 1 (SBT trang 28)

Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi \(y=f\left(x\right),y=g\left(x\right),y=h\left(x\right)\) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lại vào thời gian x. Qua biểu đồ, hãy :

a) Tìm tập xác của mỗi hàm số đã nêu ?

b) Tìm các giá trị \(f\left(2002\right);g\left(1999\right);h\left(2000\right)\) và nêu ý nghĩa của chúng ?

c) Tính hiệu \(h\left(2002\right)-h\left(1999\right)\) và nêu ý nghĩa của nó ?

 

Hướng dẫn giải

a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.

Bài 2 (SGK trang 38)

Cho hàm số :

               \(y=\left\{{}\begin{matrix}x+1;\left(x\ge2\right)\\x^2-2;\left(x< 2\right)\end{matrix}\right.\)

Tính giá trị của hàm số đó tại \(x=3;x=-1;x=2\) ?

Hướng dẫn giải

Với x ≥ 2 hàm số có công thức y= f(x) = x + 1.

Vậy giá trị của hàm số tại x = 3 là f(3) = 3 + 1 = 4.

Tương tự, với x < 2 hàm số có công thức y = f(y) = x² - 2.

Vậy f(- 1) = (- 1)² – 2 = - 1.

Tại x = 2 giá trị của hàm số là: f(2) = 2 + 1 = 3.

Trả lời: f(3) = 4; f(- 1) = - 1; f(2) = 3.

Bài 3 (SGK trang 39)

Cho hàm số \(y=3x^2-2x+1\)

Các điểm sau đó thuộc đồ thị của hàm số đó không ?

a. \(M\left(-1;6\right)\)

b. \(N\left(1;1\right)\)

c. \(P\left(0;1\right)\)

Hướng dẫn giải

a) Điểm A(x₀;y₀) thuộc đồ thị (G) của hàm số y = f(x) có tập xác định D khi và chỉ khi: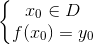

Tập xác định của hàm số y = 3x² – 2x + 1 là D = R.

Ta có : -1 ∈ R, f(- 1) = 3(- 1)² – 2(- 1) + 1 = 6

Vậy điểm M(- 1;6) thuộc đồ thị hàm số đã cho.

b) Ta có: 1 ∈ R, f(1) = 3 (1)² – 2(1) + 1 = 2 ≠ 1.

Vậy N(1;1) không thuộc đồ thị đã cho.

c) P(0;1) thuộc đồ thị đã cho.

Bài 4 (SGK trang 39)

Xét tính chẵn lẻ của các hàm số :

a. \(y=\left|x\right|\)

b. \(y=\left(x+2\right)^2\)

c. \(y=x^3+x\)

d. \(y=x^2+x+1\)

Hướng dẫn giải

a) Tập xác định của y = f(x) = |x| là D = R.

∀x ∈ R => -x ∈ R

f(- x) = |- x| = |x| = f(x)

Vậy hàm số y = |x| là hàm số chẵn.

b) Tập xác định của

y = f(x) = (x + 2)² là R.

x ∈ R => -x ∈ R

f(- x) = (- x + 2)² = x² – 4x + 4 ≠ f(x)

f(- x) ≠ - f(x) = - x² – 4x - 4

Vậy hàm số y = (x + 2)² không chẵn, không lẻ.

c) D = R, x ∈ D => -x ∈ D

f(– x) = (– x³) + (– x) = - (x³ + x) = – f(x)

Vậy hàm số đã cho là hàm số lẻ.

d) Hàm số không chẵn cũng không lẻ.

Bài 2 (SBT trang 29)

Tìm tập xác định của các hàm số ?

a) \(y=-x^5+7x-3\)

b) \(y=\dfrac{3x+2}{x-4}\)

c) \(y=\sqrt{4x+1}-\sqrt{-2x+1}\)

d) \(y=\dfrac{\sqrt{x+9}}{x^2+8x-20}\)

e) \(y=\dfrac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)

f) \(y=\dfrac{7+x}{x^2+2x-5}\)

Hướng dẫn giải

a) TXĐ: \(D=R\).
b) \(TXD=D=R\backslash\left\{4\right\}\)
c) Đkxđ: \(\left\{{}\begin{matrix}4x+1\ge0\\-2x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{-1}{4}\\x\le\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-1}{4}\le x\le\dfrac{1}{2}\).
TXĐ: D = \(\left[\dfrac{-1}{4};\dfrac{1}{2}\right]\)

Bài 3 (SBT trang 29)

Cho hàm số : 

                    \(y=f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2x-3}{x-1};\left(x\le0\right)\\-x^2+2x;\left(x>0\right)\end{matrix}\right.\)

Tính giá trị của hàm số đó tại \(x=5;x=-2;x=0;x=2\) ?

Hướng dẫn giải

\(f\left(5\right)=-5^2+2.5=-15\)
\(f\left(-2\right)=-\left(-2\right)^2+2.\left(-2\right)=-8\)
\(f\left(2\right)=-2^2+2.2=0\)

Bài 4 (SBT trang 29)

Cho các hàm số \(f\left(x\right)=x^2+2+\sqrt{2-x};g\left(x\right)=-2x^3-3x+5\)

                           \(u\left(x\right)=\left\{{}\begin{matrix}\sqrt{3-x};\left(x< 2\right)\\\sqrt{x^2-4};\left(x\ge2\right)\end{matrix}\right.\)

                          \(v\left(x\right)=\left\{{}\begin{matrix}\sqrt{6-x};\left(x\le0\right)\\x^2+1;\left(x>0\right)\end{matrix}\right.\)

Tính các giá trị \(f\left(-2\right)-f\left(1\right);f\left(-7\right)-g\left(-7\right);f\left(-1\right)-u\left(-1\right);u\left(3\right)-v\left(3;\right)v\left(0\right)-g\left(0\right);\dfrac{f\left(2\right)-f\left(-2\right)}{v\left(2\right)-v\left(-3\right)}\) ?

Hướng dẫn giải

\(f\left(-2\right)-f\left(1\right)=\left(-2\right)^2+2+\sqrt{2-\left(-2\right)}-\left(1^2+2+\sqrt{2-1}\right)\) \(=8-4=4\).
\(f\left(-7\right)-g\left(-7\right)=\left(-7\right)^2+2+\sqrt{2-\left(-7\right)}-\left(-2.\left(-7\right)^3-3.\left(-7\right)+5\right)=-658\)

Bài 5 (SBT trang 29)

Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng ?

a) \(y=-2x+3\) trên  R

b) \(y=x^2+10x+9\) trên \(\left(-5;+\infty\right)\)

c) \(y=-\dfrac{1}{x+1}\) trên \(\left(-3;-2\right)\) và \(\left(2;3\right)\)

Hướng dẫn giải

a) Hàm số \(y=-2x+3\) có a = -2 < 0 nên hàm số nghịch biến trên R.
b. Xét tỉ số \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\left(x^2_1+10x_1+9\right)-\left(x^2_2+10x_2+9\right)}{x_1-x_2}\)
\(=\dfrac{\left(x_1-x_2\right)\left(x_1+x_2+10\right)}{x_1-x_2}=x_1+x_2+10\).
Với \(x_1;x_2\notin\left(-5;+\infty\right)\) thì \(x_1+x_2+10\ge0\) nên hàm số y đồng biến trên \(\left(-5;+\infty\right)\).
c) Xét tỉ số: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-\dfrac{1}{x_1+1}+\dfrac{1}{x_2+1}}{x_1-x_2}=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Trên \(\left(-3;-2\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}< 0\) nên hàm số y nghịch biến trên \(\left(-3;-2\right)\).
Trên \(\left(2;3\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}>0\) nên hàm số y đồng biến trên \(\left(2;3\right)\).

Bài 6 (SBT trang 29)

Xét tính chẵn, lẽ của các hàm số :

a) \(y=-2\)

b) \(y=3x^2-1\)

c) \(y=-x^4+3x-2\)

d) \(y=\dfrac{-x^4+x^2+1}{x}\)

Hướng dẫn giải

lời giải

a) Hàm chẵn

b) f(x) =f(-x)=>hàm chẵn

c) không chẵn, không lẻ

d)f(-x) =\(\dfrac{-x^4+x^2+1}{-x}=-\dfrac{-x^4+x^2+1}{x}=-f\left(x\right)\) =>hàm lẻ