§1. Hàm số
Bài 1 trang 28 Sách bài tập (SBT) Toán Đại số 10
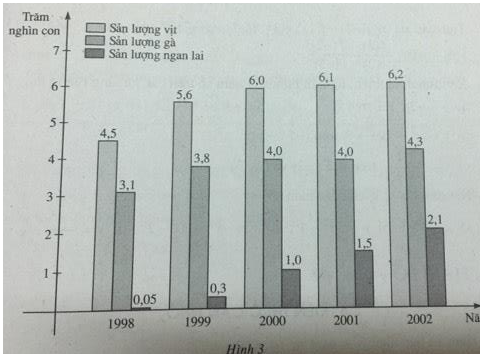
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi \(y = f(x),y = g(x)\) và \(y = h(x)\) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:
a) Tìm tập xác định của mỗi hàm số đã nêu.
b) Tìm các giá trị f(2002), g(1999), h(2000) và nêu ý nghĩa của chúng;
c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.
Hướng dẫn giải
a) Tập xác định của cả ba hàm số \(y = f(x),y = g(x)\) và \(y = h(x)\) là:
\(D = {\rm{\{ }}1998;1999;2000;2001;2002\} \)
b) \(f(2002) = 620000\) (con) \(g(1999) = 380000\) (con) \(h(2000) = 100000\) (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.
c) \(h(2002) - h(1999) = 210000 - 30000 = 180000\) (con)
Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.
Bài 2 trang 29 Sách bài tập (SBT) Toán Đại số 10
Tìm tập xác định của các hàm số
a) \(y = - {x^5} + 7x - 2\)
b) \(y = {{3x + 2} \over {x - 4}}\)
c) \(y = \sqrt {4x + 1} - \sqrt { - 2x + 1} \)
d) \(y = {{\sqrt {x + 9} } \over {{x^2} + 8x - 20}}\)
e) \(y = {{2x + 1} \over {(2x + 1)(x - 3)}}\)
h) \(y = {{7 + x} \over {{x^2} + 2x - 5}}\)
Hướng dẫn giải
a) D = R;
b) D = R\{4};
c) Hàm số xác định với các giá trị của x thỏa mãn
\(4x + 1 \ge 0\) và \( - 2x + 1 \ge 0\) hay \(x \ge - {1 \over 4}\) \(x \le - {1 \over 2}\)
Vậy tập xác định của hàm số đã cho là \(D = {\rm{[}} - {1 \over 4};{1 \over 2}{\rm{]}}\)
d) Hàm số xác định với các giá trị của x thỏa mãn
\(\left\{ \matrix{
x + 9 \ge 0 \hfill \cr
{x^2} + 8x - 20 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge - 9 \hfill \cr
x \ne - 10,x \ne 2 \hfill \cr} \right.\)
Vậy tập xác định của hàm số đã cho là \(D = {\rm{[ - 9; + }}\infty )\backslash {\rm{\{ }}2\} \)
e) \(D = R\backslash {\rm{\{ - }}{1 \over 2};3\} \)
h) \(D = R\backslash {\rm{\{ }} - 1 - \sqrt 6 ; - 1 + \sqrt 6 \} \) vì
\({x^2} + 2x - 5 = 0 \Leftrightarrow \left[ \matrix{
x = - 1 - \sqrt 6 \hfill \cr
x = - 1 + \sqrt 6 \hfill \cr} \right.\)
Bài 3 trang 29 Sách bài tập (SBT) Toán Đại số 10
\(y = f(x) = \left\{ \matrix{
{{2x - 3} \over {x - 1}};x \le 0 \hfill \cr
- {x^2} + 2x;x > 0 \hfill \cr} \right.\)
Tính giá trị của hàm số đó tại \(x = 5;x = - 2;x = 0;x = 2\)
Hướng dẫn giải
\(f(5) = - {5^2} + 2.5 = - 25 + 10 = - 15\) (vì 5 > 0);
\(f( - 2) = {{2.( - 2) - 3} \over { - 2 - 1}} = {7 \over 3}\) (vì -2<0); \(f(0) = 3;f(2) = 0\).
Bài 4 trang 29 Sách bài tập (SBT) Toán Đại số 10
Cho các hàm số
\(f(x) = {x^2} + 2 + \sqrt {2 - x} ;g(x) = - 2{x^3} - 3x + 5\);
\(u(x) = \left\{ \matrix{
\sqrt {3 - x} ,x < 2 \hfill \cr
\sqrt {{x^2} - 4} ,x \ge 2 \hfill \cr} \right.\);
\(v(x) = \left\{ \matrix{
\sqrt {6 - x} ,x \le 0 \hfill \cr
{x^2} + 1,x > 0 \hfill \cr} \right.\)
Tính các giá trị
\(f( - 2) - f(1);g(3);f( - 7) - g( - 7);f( - 1) - u( - 1);u(3) - v(3);v(0) - g(0);{{f(2) - f( - 2)} \over {v(2) - v( - 3)}}\)
Hướng dẫn giải
\(f( - 2) - f( - 1) = {( - 2)^2} + 2 + \sqrt {2 + 2} - ({1^2} + 2 + \sqrt {2 - 1} ) = 8 - 4 = 4\);
\(g(3) = - {2.3^3} - 3.3 + 5 = - 58\);
\(f( - 7) - g( - 7) = {( - 7)^2} + 2 + \sqrt {2 + 7} - {\rm{[}} - 2.{( - 7)^3} - 3.( - 7) + 5] = - 658\);
\(f( - 1) - u( - 1) = 3 + \sqrt 3 - 2 = 1 + \sqrt 3 \);
\(u(3) - v(3) = \sqrt {9 - 4} - (9 + 1) = \sqrt 5 - 10\);
\(v(0) - g(0) = \sqrt 6 - 5\);
\({{f(2) - f( - 2)} \over {v(2) - v( - 3)}} = {{6 - 8} \over {5 - 3}} = - 1\)
Bài 5 trang 30 Sách bài tập (SBT) Toán Đại số 10
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
a) \(y = - 2x + 3\) trên R
b) \(y = {x^2} + 10x + 9\) trên \(( - 5; + \infty )\)
c) \(y = - {1 \over {x + 1}}\) trên (-3; -2) và (2; 3).
Hướng dẫn giải
a) \(\forall {x_1},{x_2} \in R\) ta có:
\(f({x_1}) - f({x_2}) = - 2{x_1} + 3 - ( - 2{x_2} + 3) = - 2({x_1} - {x_2})\)
Ta thấy \({x_1} > {x_2}\) thì \(2({x_1} - {x_2}) < 0\) tức là:
\(f({x_1}) - f({x_2}) < 0 \Leftrightarrow f({x_1}) < f({x_2})\)
Vậy hàm số đã cho nghịch biến trên R.
b) \(\forall {x_1},{x_2} \in R\), ta có
\(f({x_1}) - f({x_2}) = x_1^2 + 10{x_1} + 9 - x_2^2 - 10{x_2} - 9\)
= \(({x_1} - {x_2})({x_1} + {x_2}) + 10({x_1} - {x_2})\)
= \(({x_1} - {x_2})({x_1} + {x_2} + 10)\) (*)
\(\forall {x_1},{x_2} \in ( - 5; + \infty )\) và \({x_1} < {x_2}\) ta có \({x_1} - {x_2} < 0\) và \({x_1} + {x_2} + 10 > 0\) vì
\({x_1} > - 5;{x_2} > - 5 = > {x_1} + {x_2} > - 10\)
Vậy từ (*) suy ra \(f({x_1}) - f({x_2}) < 0 \Leftrightarrow f({x_1}) < f({x_2})\)
Hàm số đồng biến trên khoảng \(( - 5; + \infty )\)
c) \(\forall {x_1},{x_2} \in ( - 3; - 2)\) và \({x_1} < {x_2}\), ta có
\({x_1} - {x_2} < 0;{x_1} + 1 < - 2 + 1 < 0;{x_2} + 1 < - 2 + 1 < 0 = > ({x_1} + 1)({x_2} + 1) > 0\). Vậy
\(f({x_1}) - f({x_2}) = - {1 \over {{x_1} + 1}} + {1 \over {{x_2} + 1}} = {{{x_1} - {x_2}} \over {({x_1} + 1)({x_2} + 1)}} < 0 \Leftrightarrow f({x_1}) < f({x_2})\)
Do đó hàm số đồng biến trên khoảng (-3; -2)
\(\forall {x_1},{x_2} \in ( - 3; - 2)\) và \({x_1} < {x_2}\) , tương tự ta cũng có \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến trên khoảng (2;3).
Bài 6 trang 30 Sách bài tập (SBT) Toán Đại số 10
Xét tính chẵn, lẻ của các hàm số
a) y= -2;
b) \(y = 3{x^2} - 1\)
c) \(y = - {x^4} + 3x - 2\)
d) \(y = {{ - {x^4} + {x^2} + 1} \over x}\)
Hướng dẫn giải
a) Tập xác định D = R và \(\forall x \in D\) có \( - x \in D\) và \(f( - x) = - 2 = f(x)\)
Hàm số là hàm số chẵn.
b) b)Tập xác định D = R ; \(\forall x \in D\) có \( - x \in D\) và \(f( - x) = 3.{( - x)^2} - 1 = 3{x^2} - 1 = f(x)\)
Vậy hàm số đã cho là hàm số chẵn.
c) Tập xác định D = R, nhưng \(f(1) = - 1 + 3 - 2 = 0\) còn \(f( - 11) = - 1 - 3 - 2 = - 6\) nên \(f( - 1) \ne f(1)\) và \(f( - 1) \ne - f(1)\)
Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.
d) Tập xác định D = R\{0} nên nếu \(x \ne 0\) và \(x \in D\) thì \( - x \in D\) . Ngoài ra
\(f( - x) = {{ - {{( - x)}^4} + {{( - x)}^2} + 1} \over { - x}} = {{ - {x^4} + {x^2} + 1} \over { - x}} = {{ - {x^4} + {x^2} + 1} \over x} = - f(x)\) .
Vậy hàm số đã cho là hàm số lẻ.




