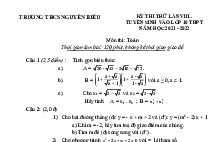Đề thi và lời giải chi tiết Kỳ thi HSG lớp 9 Sở Giáo dục và Đào tạo Vĩnh Phúc

ĐỀ THI CHỌN HSG TỈNH VĨNH PHÚC NĂM HỌC 2017-2018  a  2018 a  2018  a  1  . Câu 1: Rút gọn biểu thức P    a  1  2 a  a  2 a 1  z z Câu 2: Cho ba số thực dương x, y,z thỏa mãn x  y  và y  z. Chứng minh đẳng thức  y x x y x y z  2 , x y z 2 2  x z . y z Câu 3: Tìm số tự nhiên abcd sao cho abcd  abc  ab  a  4321. ( m  1 )x  y  2 Câu 4: Cho hệ phương trình  ( m là tham số và x, y là ẩn số)  x  2y  2 Tìm tất cả các giá trị nguyên của m để hệ phương trình có nghiệm ( x, y ) trong đó x, y là các số nguyên. Câu 5: Giải phương trình 1  x  4  x  3. Câu 6: Cho tam giác ABC vuông tại A, AB  12cm, AC  16cm. Gọi I là giao điểm các đường phân giác trong của tam giác ABC, M là trung điểm của cạnh BC . Chứng minh rằng đường thẳng BI vuông góc với đường thẳng MI. Câu 7: Cho hình thoi ABCD có góc BAD  500 , O là giao điểm của hai đường chéo. Gọi H là chân đường vuông góc kẻ từ O đến đường thẳng AB. Trên tia đối của tia BC lấy điểm M ( điểm M không trùng với điểm B), trên tia đối của tia DC lấy điểm N sao cho đường thẳng HM song song với đường thẳng AN. a) Chứng minh rằng: MB.DN  BH.AD b) Tính số đo góc MON Câu 8: Cho đường tròn (O) cố định và hai điểm phân biệt B, C cố định thuộc đường tròn ( O ). Gọi A là một điểm thay đổi trên đường tròn (O) (điểm A không trùng với điểm B và C), M là trung điểm của đoạn thẳng AC. Từ điểm M kẻ đường thẳng (d) vuông góc với đường thẳng AB, đường thẳng (d) cắt đường thẳng AB tại điểm H. Chứng minh rằng khi điểm A thay đổi trên đường tròn (O) thì điểm H luôn nằm trên một đường tròn cố định. 1 1 1    2 . Chứng a b c 1 1 1 2    . 2 2 2 2 2 2 3 5a  2ab  2b 5b  2bc  2c 5c  2ca  2a Câu 9: Cho a,b,c là các số thực dương thoả mãn điều kiện minh rằng: Câu 10: Cho hình vuông ABCD và 2018 đường thẳng thỏa mãn đồng thời hai điều kiện: 1) Mỗi đường thẳng đều cắt hai cạnh đối của hình vuông. 2) Mỗi đường thẳng đều chia hình vuông thành hai phần có tỉ lệ diện tích bằng 1 . 3 Chứng minh rằng trong 2018 đường thẳng đó có ít nhất 505 đường thẳng đồng quy. LỜI GIẢI ĐỀ THI HSG TỈNH VĨNH PHÚC NĂM HỌC 2017-2018  a  2018 a  2018  a  1  . Câu 1: Rút gọn biểu thức P    a  1  2 a  a  2 a 1 a  0 a  1 Điều kiện:   a  2018  a 1 a  2018   2 ( a  1)( a  1)  2 a  ( a  1) Khi đó: P    ( a  2018 )( a  1)  ( a  2018 )( a  1) a  1 . ( a  1)2 ( a  1) 2 a  2.2017 a a  1 2017 .  2 a 1 ( a  1) ( a 1) 2 a Câu 2: Cho ba số thực dương x, y,z thỏa mãn x  y  và y  z. Chứng minh đẳng thức  y x  x y z  z x z 2 y 2   x  z   x  y  z  y Ta có: y y  z  x  y  z  x  x  2 y  z  x  z    x  z      2 x  y  z  y  z    y  z   x   2 , x y z x z . y z  z z  2 z  2 2 2 x z 2 2 2 y 2 2 x 2 y  z x 2 y 2 z x 2 y 2 x z . y z Câu 3: Tìm số tự nhiên abcd sao cho abcd  abc  ab  a  4321. Ta có: abcd  abc  ab  a  4321  1111a  111b  11c  d  4321 Vì a,b,c,d  1 và 1  a  9,0  b,c,d  9 nên 3214  1111a  4321  a  3 . Thay vào (1) ta được: 111b  11c  d  988 2 Lập luận tương tự ta có: 880  111b  988  b  8 . Thay vào (2) ta được: 11c  d  100 Mà 91  11c  100  c  9 và d  1 . ( m  1 )x  y  2 Câu 4: Cho hệ phương trình  ( m là tham số và x, y là ẩn số)  x  2y  2 Tìm tất cả các giá trị nguyên của m để hệ phương trình có nghiệm ( x, y ) trong đó x, y là các số nguyên. Từ phương trình thứ hai ta có: x  2  2 y thế vào phương trình thứ nhất được: ( m  1)( 2  2y )  y  2  ( 2m  3 )y  2m  4 (3) Hệ có nghiệm x, y là các số nguyên  ( 3 ) có nghiệm y là số nguyên. Với m  y  2m  3  0  ( 3 ) có nghiệm y  2m  4 1  1 2m  3 2m  3  2m  3  1 m  2   . Vậy có 2 giá trị m thoả mãn là 1; 2.  2m  3  1 m  1 Câu 5: Giải phương trình 1  x  4  x  3. 1  x  0  4  x  1 *  4  x  0 Điều kiện xác định  Với điều kiện (*), phương trình đã cho tương đương với: 5  2 1  x. 4  x  9  1  x  4  x   2  1  x  4  x   4  x2  3x  0 x  0  x  x  3  0   . Đối chiếu với điều kiện (*) ta được x  0; x  3.  x  3 Câu 6: Cho tam giác ABC vuông tại A, AB  12cm, AC  16cm. Gọi I là giao điểm các đường phân giác trong của tam giác ABC, M là trung điểm của cạnh BC . Chứng minh rằng đường thẳng BI vuông góc với đường thẳng MI. Ta có BC  AB2  AC 2  20cm . Gọi E là giao điểm của BI với AC. AE EC AE  EC 1 BC Theo tính chất đường phân giác ta có:     EC   10cm AB BC AB  BC 2 2 Ta có ICE  ICM( c  g  c ) do: EC  MC  10 ; ICE  ICM ; IC chung. Suy ra: IEC  IMC  IEA  IMB Mặt khác IBM  IBA  hai tam giác IBM , ABE đồng dạng  BIM  BAE  900  BI  MI Câu 7: Cho hình thoi ABCD có góc BAD  500 , O là giao điểm của hai đường chéo. Gọi H là chân đường vuông góc kẻ từ O đến đường thẳng AB. Trên tia đối của tia BC lấy điểm M (điểm M không trùng với điểm B), trên tia đối của tia DC lấy điểm N sao cho đường thẳng HM song song với đường thẳng AN. a) Chứng minh rằng: MB.DN  BH.AD b) Tính số đo góc MON a) Ta có MBH  ADN ,MHB  AND MB BH  MB.DN  BH .AD ( 1)  AD DN BH OB b) Ta có: OHB ∽  AOD    DO.OB  BH .AD  2  DO AD MB OB Từ (1) và (2) ta có: MB.DN  DO.OB   DO DN MBH ∽  ADN  Ta lại có: MBO  1800  CBD  1800  CDB  ODN nên MBO ∽ ODN  OMB  NOD.    Từ đó suy ra: MON  1800  MOB  NOD  1800  MOB  OMB   1800  OBC  1150 Câu 8: Cho đường tròn (O) cố định và hai điểm phân biệt B, C cố định thuộc đường tròn ( O ). Gọi A là một điểm thay đổi trên đường tròn (O) (điểm A không trùng với điểm B và C), M là trung điểm của đoạn thẳng AC. Từ điểm M kẻ đường thẳng (d) vuông góc với đường thẳng AB, đường thẳng (d) cắt đường thẳng AB tại điểm H. Chứng minh rằng khi điểm A thay đổi trên đường tròn (O) thì điểm H luôn nằm trên một đường tròn cố định. Gọi D là trung điểm của đoạn BC, vì tam giác BOC, AOC là các tam giác cân tại O nên OD  BC,OM  AC . Ta có: ODC  OMC  90  Bốn điểm O, D, C, M cùng nằm trên đường tròn ( I ) có tâm I 0 cố định, đường kính OC cố định. Gọi E là điểm đối xứng với D qua tâm I, khi đó E cố định và DE là đường kính của đường tròn ( I ). Nếu H  E,H  B : - Với M  E  BHE  90 0 - Với M  E , do DM BH  DMH  900 . Khi đó DME  DMH  900  H ,M ,E thẳng hàng. Suy ra BHE  90 0 Vậy ta luôn có: BHE  90 hoặc H  E hoặc H  B do đó H thuộc đường tròn đường kính BE cố định. 0 1 1 1    2 . Chứng minh rằng: a b c 1 1 1 2    . 5a 2  2ab  2b 2 5b 2  2bc  2c 2 5c 2  2ca  2a 2 3 Câu 9: Cho a,b,c là các số thực dương thoả mãn điều kiện Với x, y,z  0 ta có : x  y  z  3 3 xyz , x yz 1 1 1 1    33 x y z xyz  1 1 1 1 1 1 1 1   x  y  z     9       Đẳng thức xảy ra khi x yz 9 x y z x y z Ta có: 5a 2  2ab  2b2  ( 2a  b )2  ( a  b )2  ( 2a  b )2  1  1 1 1 1 1      . Đẳng thức xảy ra khi a  b 2a  b 9  a a b  5a  2ab  2b 1 1 1 1 1 1 Tương tự:       Đẳng thức xảy ra khi b  c 2 2 2b  c 9  b b c  5b  2bc  2c 1 1 11 1 1       Đẳng thức xảy ra khi c  a 5c 2  2ca  2a 2 2c  a 9  c c a  Do đó: 1 1 1 13 3 3        2 2 2 2 2 2 9a b c 5a  2ab  2b 5b  2bc  2c 5c  2ca  2a 2 2 1 1 1 1 2      3 a b c 3 Đẳng thức xảy rakhi a  b  c  3 . Vậy bất đẳng thức được chứng minh. 2 Câu 10: Cho hình vuông ABCD và 2018 đường thẳng thỏa mãn đồng thời hai điều kiện: 1) Mỗi đường thẳng đều cắt hai cạnh đối của hình vuông. 2) Mỗi đường thẳng đều chia hình vuông thành hai phần có tỉ lệ diện tích bằng 1 . 3 Chứng minh rằng trong 2018 đường thẳng đó có ít nhất 505 đường thẳng đồng quy. Giả sử hình vuông ABCD có cạnh là a ( a>0). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Gọi d là một đường thẳng bất kỳ trong 2018 đường thẳng đã cho thỏa mãn yêu cầu bài toán. Không mất tính tổng quát, giả sử d cắt các đoạn thẳng AD, MP, BC lần lượt tại S, E, K sao cho SCDSK  3S ABKS Từ SCDSK  3S ABKS ta suy ra được: DS  CK  3  AS  BK   a  AS  a  BK  3  AS  BK   AS  BK   EM  1 a 2 1 a suy ra E cố định và d đi qua E. 4 Lấy F, H trên đoạn NQ và G trên đoạn MP sao cho FN  GP  HQ  a . 4 Lập luận tương tự như trên ta có các đường thẳng thỏa mãn điều kiện của đề bài phải đi qua một trong bốn điểm cố định E, F, G, H. Theo nguyên lý Dirichlet từ 2018 đường thẳng thỏa mãn điều kiện của đề bài phải có ít nhất  2018   4   1  505 đường thẳng đi qua một trong bốn điểm E, F, G, Hcố định, nghĩa là 505 đường thẳng đó đồng quy.