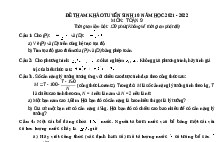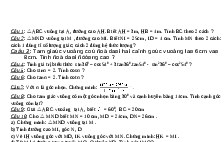Đề ôn tập HSG Toán 9
Nội dung tài liệu
Tải xuống
Link tài liệu:
Các tài liệu liên quan
-
![Đề cương ôn thi học kì 2 Toán 9 năm 2021-2022]()
-
![Chuyên đề ôn thi HSG Toán 9: Phương trình nghiệm nguyên]()
-
![Các bài toán hay tự luyện cho kì thi tuyển sinh vào 10]()
-
![Đề tham khảo ôn tập vào 10]()
-
![Đề tham khảo ôn tập tuyển sinh vào 10]()
-
![Các bài toán hay tự ôn vào 10]()
-
![280 bài toán nâng cao ôn thi HSG Toán 9]()
-
![Chuyên đề ôn thi HSG hình học Toán 9: ĐƯỜNG TRÒN – DÂY CUNG – TIẾP TUYẾN CỦA ĐƯỜNG TRÒN]()
-
![Các bài toán tiêu biểu ôn thi HSG Toán 9]()
-
![Các bài tập hình học hay lớp 9]()
Có thể bạn quan tâm
Thông tin tài liệu
ĐỀ ÔN TẬP HSG LỚP 9
Câu 1.
a) Cho
là các số dương và thỏa mãn đẳng thức
.
Chứng minh rằng:
b) Giả sử các số
thỏa mãn
và
.
Chứng minh rằng:
Câu 2.
a) Chứng minh rằng nếu
là các số nguyên dương thỏa mãn
b) Tìm tất cả các số nguyên dương
thỏa mãn phương trình
n
c) Tìm số tự nhiên n để 2 + 15 là số chính phương.
Câu 3.
1. Cho
a)
thì
.
.
là các số dương. Chứng minh rằng:
.
b)
.
2
2
2
2. Cho a, b, c là các số thực thỏa mãn a + b + c = 1.
Chứng minh rằng abc + 2(1 + a + b + c + ab + ac + bc) ≥ 0.
3. Cho 3 số thực dương a,b,c thỏa mãn
. Tìm giá trị nhỏ nhất của biểu thức
Câu 4 .
1. Cho ∆ABC vuông ở A (AB < AC). Biết BC =
và bán kính đường tròn nội tiếp
∆ABC bằng 2. Tính số đo góc B và góc C của ∆ABC.
2. Cho tam giác ABC vuông tại A. Vẽ ra phía ngoài tam giác đó các tam giác ABD vuông
cân tại B, ACF vuông cân tại C. Gọi H là giao điểm của AB và CD, K là giao điểm của AC
và BF. Kẻ DM vuông góc với BC, FN vuông góc với BC.
a) Chứng minh DM + FN = BC.
b) Chứng minh AH = AK.
Câu 5. Giải các phương trình
a)
b)
Câu 1.
a) Cho
là các số dương và thỏa mãn đẳng thức
.
Chứng minh rằng:
b) Giả sử các số
thỏa mãn
và
.
Chứng minh rằng:
Câu 2.
a) Chứng minh rằng nếu
là các số nguyên dương thỏa mãn
b) Tìm tất cả các số nguyên dương
thỏa mãn phương trình
n
c) Tìm số tự nhiên n để 2 + 15 là số chính phương.
Câu 3.
1. Cho
a)
thì
.
.
là các số dương. Chứng minh rằng:
.
b)
.
2
2
2
2. Cho a, b, c là các số thực thỏa mãn a + b + c = 1.
Chứng minh rằng abc + 2(1 + a + b + c + ab + ac + bc) ≥ 0.
3. Cho 3 số thực dương a,b,c thỏa mãn
. Tìm giá trị nhỏ nhất của biểu thức
Câu 4 .
1. Cho ∆ABC vuông ở A (AB < AC). Biết BC =
và bán kính đường tròn nội tiếp
∆ABC bằng 2. Tính số đo góc B và góc C của ∆ABC.
2. Cho tam giác ABC vuông tại A. Vẽ ra phía ngoài tam giác đó các tam giác ABD vuông
cân tại B, ACF vuông cân tại C. Gọi H là giao điểm của AB và CD, K là giao điểm của AC
và BF. Kẻ DM vuông góc với BC, FN vuông góc với BC.
a) Chứng minh DM + FN = BC.
b) Chứng minh AH = AK.
Câu 5. Giải các phương trình
a)
b)