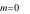Đề luyện tập Chuyên đề 1 - Ứng dụng của đạo hàm để khảo sát và vẽ đồ thị của hàm số

Những lưu ý trước khi làm bài:

• Đề thi gồm các câu hỏi thuộc nội dung Chương 1 - Giải tích 12: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số, giúp các em ôn tập và tự kiểm tra, đánh giá, từ đó có kế hoạch học tập phù hợp.

• Thời gian thi là 30 phút. Trước khi bắt đầu, hãy đảm bảo em có đủ thời gian thi; đồng thời chuẩn bị đầy đủ dụng cụ làm bài như máy tính, giấy bút... để sẵn sàng thi một cách nghiêm túc nhất. 

• Ngay sau khi nộp bài, các em sẽ được thông báo kết quả chi tiết về bài làm của mình.

Chúc các em thành công!

[NOIDUNG]

Câu 1: Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ:

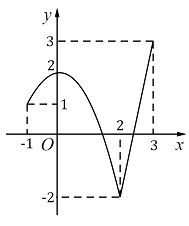
Gọi 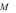và 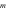lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của 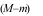bằng

A. 1.

B. 4.

C. 0.

D. 5.

Câu 2: Số giá trị nguyên của 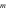để hàm số nghịch biến trên từng khoảng xác định của nó là

A. 1.

B. 2.

C. 3.

D. 4.

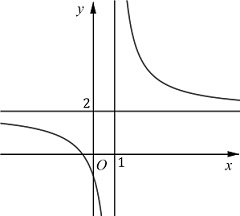
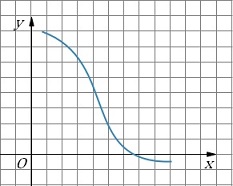
Câu 3: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

A. .

B. .

C. .

D. .

Câu 4: Cho hàm số có bảng biến thiên như sau:

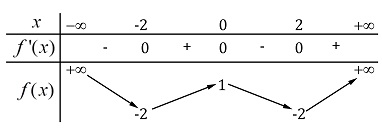
Số nghiệm thực của phương trình 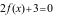là

A. 4.

B. 3.

C. 1.

D. 2.

Câu 5: Cho hàm số (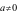) có đồ thị như hình vẽ:

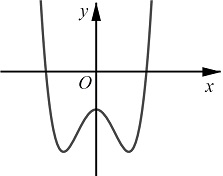
Mệnh đề nào dưới đây đúng?

A. và .

B. và .

C. và .

D. và .

Câu 6: Với giá trị nào của 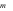thì đồ thị hàm số không có tiệm cận đứng?

A. .

B. hoặc .

C. hoặc .

D.

Câu 7: Cho hàm số có đồ thị như hình vẽ:

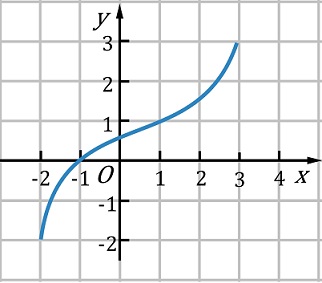
Giá trị củ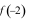a là

A. 3.

B. -2.

C. 4.

D. 1.

Câu 8: Cho hàm số xác định, liên tục trên và có bảng biến thiên như sau:

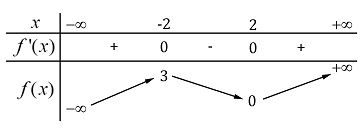
Xác định giá trị và của hàm số đã cho.

A. và .

B. và .

C. và .

D. và .

Câu 9: Cho hàm số có đồ thị 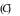là đường cong trong hình vẽ và đường thẳng 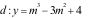(với 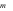là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số 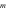để đường thẳng 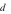cắt đồ thị tại ba điểm phân biệt?

A. 3.

B. 2.

C. 1.

D. vô số.

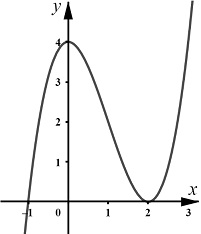
Câu 10: Đồ thị hàm số cắt trục hoành tại mấy điểm?

A. 0.

B. 2.

C. 4.

D. 3.

Câu 11: Tập xác định của hàm số 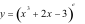là

A. .

B. .

C. .

D. .

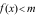Câu 12: Cho hàm số thỏa mãn . Bất phương trình có nghiệm thuộc khoảng khi và chỉ khi

A. .

B. .

C. .

D. .

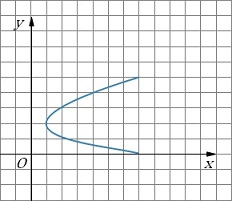
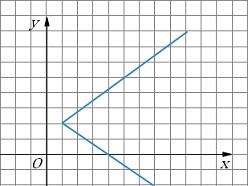
Câu 13: Đồ thị (đường màu xanh) nào sau đây biểu diễn một hàm số?

A.

B.

C.

D.

Câu 14: Cho hàm số có bảng biến thiên như sau:

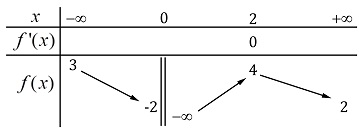
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị đã cho là

A. 4.

B. 1.

C. 2.

D. 3.

Câu 15: Cho hàm số liên tục trên đoạn và có bảng biến thiên như sau:

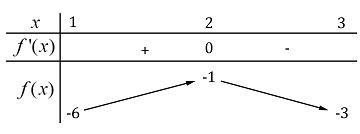
Tổng các giá trị 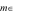sao cho phương trình 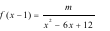có hai nghiệm phân biệt trên đoạn bằng

A. -75.

B. -72.

C. -294.

D. -297.