Chuyên đề cực trị của hàm số
Nội dung tài liệu
Tải xuốngCác tài liệu liên quan
-
![Các đề luyện thi TNTHPT môn Toán]()
-
![Chuyên đề sự đồng biến và nghịch biến]()
-
![Chuyên đề cực trị của hàm số]()
-
![Test công thức]()
-
![300 câu trắc nghiệm chương Đạo hàm theo chủ đề]()
-
![520 bài tập trắc nghiệm đạo hàm]()
-
![Đề luyện tập Chuyên đề 1 - Ứng dụng của đạo hàm để khảo sát và vẽ đồ thị của hàm số]()
-
![Đề luyện tập Chuyên đề 2 - Khối đa diện]()
-
![Đề luyện tập Chuyên đề 3 - Hàm số lũy thừa, hàm số mũ và hàm lôgarit]()
-
![ĐỀ 44-TỔNG HỢP (ĐẾN NGUYÊN HÀM-MẶT CẦU)]()
Có thể bạn quan tâm
Thông tin tài liệu
CHUYÊN ĐỀ CỰC TRỊ
A. KIẾN THỨC CƠ BẢN
1. Định nghĩa: Cho hàm số  xác định và liên tục trên khoảng
xác định và liên tục trên khoảng  và điểm
và điểm  .
.
+ Nếu tồn tại số 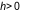 sao cho
sao cho 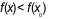 với mọi
với mọi  và
và 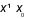 thì ta nói hàm số
thì ta nói hàm số 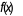 đạt cực đại tại
đạt cực đại tại 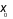 .
.
+ Nếu tồn tại số 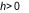 sao cho
sao cho 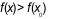 với mọi
với mọi  và
và 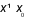 thì ta nói hàm số
thì ta nói hàm số 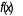 đạt cực tiểu tại
đạt cực tiểu tại 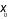 .
.
2. Điều kiện đủ để hàm số có cực trị: Giả
sử hàm số  liên tục trên
liên tục trên  và
có đạo hàm trên
và
có đạo hàm trên 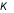 hoặc trên
hoặc trên  ,
với
,
với 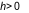 .
.
+ Nếu  trên khoảng
trên khoảng  và
và  trên
trên 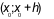 thì
thì 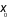 là một điểm cực đại của hàm số
là một điểm cực đại của hàm số 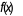 .
.
+ Nếu  trên khoảng
trên khoảng  và
và  trên
trên 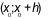 thì
thì 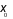 là một điểm cực tiểu của hàm số
là một điểm cực tiểu của hàm số 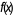 .
.
Minh họa bằng bảng biến thiến
3. Những khái niệm cơ bản về cực trị :
+ Điểm cực đại , cực tiểu của đồ thị : xét đồ thị hàm số trong hình vẽ dưới, ta có điểm A được gọi là cực đại của đồ thị , điểm B là điểm cực tiểu của đồ thị . điểm cực đại , cực tiểu của đồ thị hàm số được gọi chung là điểm cực trị của đồ thị hàng số đó .
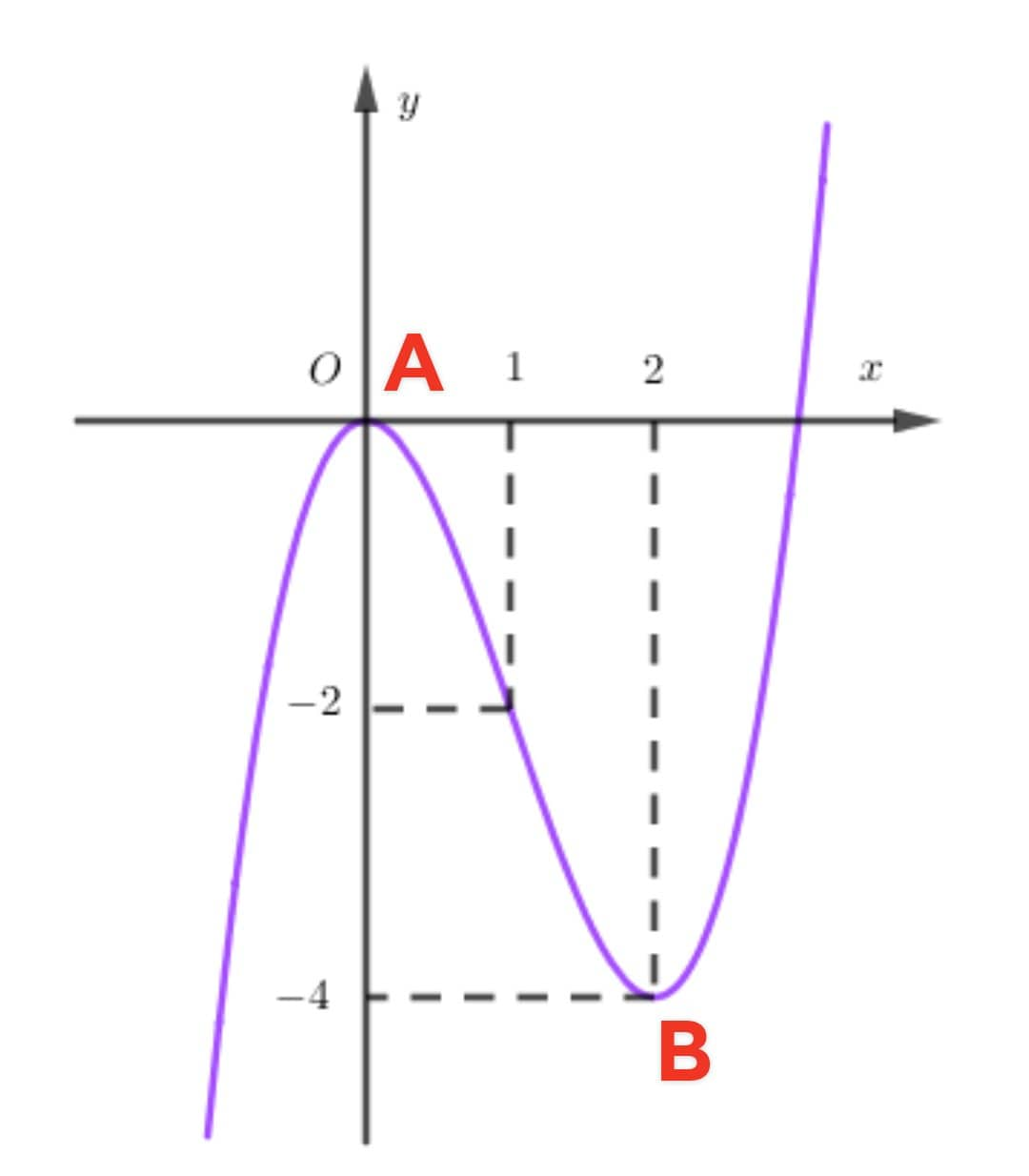
B. CÁC QUY TẮC TÌM CỰC TRỊ
1. Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính  .
Tìm các điểm tại đó
.
Tìm các điểm tại đó  bằng 0 hoặc
bằng 0 hoặc  không xác định.
không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính .
Giải phương trình
.
Giải phương trình  và ký hiệu
và ký hiệu
 là các nghiệm.
là các nghiệm.
Bước 3.Tính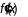 và
và 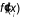 .
.
Bước 4. Dựa vào dấu của 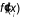 suy ra tính chất cực trị của điểm
suy ra tính chất cực trị của điểm 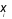 .
.
C. BÀI TẬP TỰ LUYỆN
Cho hàm số
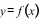 có bảng biến thiên như sau hàm số đạt cực tiểu tại x0
bằng:
có bảng biến thiên như sau hàm số đạt cực tiểu tại x0
bằng:
A.  B.
B.  C.
C. 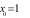 D.
D. 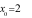
Cho hàm số y = f (x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
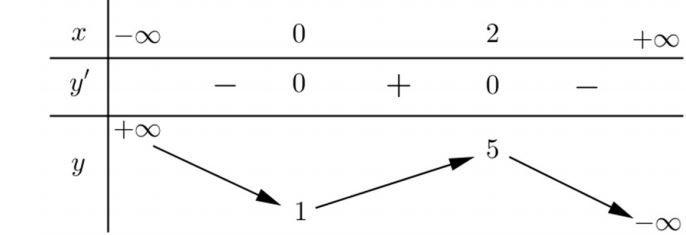
A. 1 B. 2 C. 0 D. 5
Cho hàm số
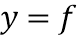 có bảng biến thiên như sau:
có bảng biến thiên như sau: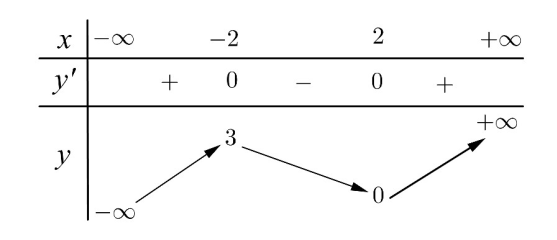
Tìm giá trị cực đại 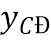 và giá trị cực tiểu
và giá trị cực tiểu 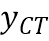 của hàm số đã cho.
của hàm số đã cho.
A. 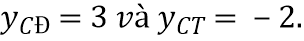 B.
B. 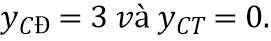
C. 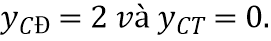 D.
D. 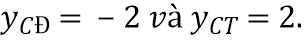
Cho hàm số
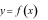 xác định, liên tục trên
xác định, liên tục trên  và có bảng biến thiên:
và có bảng biến thiên:
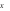 |
 |
1 | 2 |  |
|||
|---|---|---|---|---|---|---|---|
 |
 |
+ | 0 |  |
|||
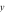 |
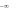 |
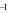 |
0 | ||||
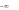 |
|||||||
Tọa độ điểm cực đại của đồ thị hàm số là
A.  B.
B.  C.
C.  D.
D. 
Cho hàm số
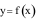 có bảng biến thiên như hình bên. Mệnh đề nào dưới đây
đúng?
có bảng biến thiên như hình bên. Mệnh đề nào dưới đây
đúng?
| x | - |
0 | 2 | + |
|||
|---|---|---|---|---|---|---|---|
| y’ | + | 0 | - | 0 | + | ||
| y | - |
5 | 1 | + |
A. Hàm số đạt cực đại tại x = 5. B. Hàm số không có cực trị.
C. Hàm số đạt cực tiểu tại x = 1. D. Hàm số đạt cực đại tại x = 0.
Cho hàm số
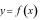 có đồ thị như hình vẽ. Đồ thị hàm số
có đồ thị như hình vẽ. Đồ thị hàm số  có
mấy điểm cực trị?
có
mấy điểm cực trị?
A. 0 B. 2 C. 1 D. 3
Cho hàm số
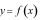 có đồ thị như hình vẽ. Tìm kết luận đúng
có đồ thị như hình vẽ. Tìm kết luận đúng
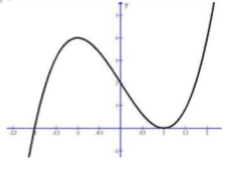
A. Hàm số 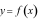 có điểm cực tiểu là
có điểm cực tiểu là 
B. Hàm số 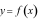 có giá trị cực đại là -1.
có giá trị cực đại là -1.
C. Hàm số 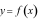 có điểm cực đại là
có điểm cực đại là 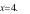
D. Hàm số 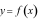 có giá trị cực tiểu là 0.
có giá trị cực tiểu là 0.
Hàm số
 có điểm cực đại là:
có điểm cực đại là:
A. B.
B.  5
C.
5
C.  3
D.
3
D.  0
0
Cho hàm số
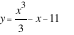 .
Giá trị cực tiểu của hàm số là
.
Giá trị cực tiểu của hàm số là
A.2. B.  C.
C.  D. -1.
D. -1.
Đồ thị hàm số
 có điểm cực tiểu là
có điểm cực tiểu là
A. B.
B.  C.
C.  D.
D. 
Cho hàm số
 Tọa độ của điểm cực đại của đồ thị hàm số là:
Tọa độ của điểm cực đại của đồ thị hàm số là:
A. B.
B.  C.
C.  D.
D. 
Gọi
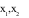 là hai điểm cực trị của hàm số
là hai điểm cực trị của hàm số  .
Giá trị của
.
Giá trị của 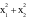 bằng:
bằng:
A. 13 B. 32 C. 4 D. 36
Hàm số
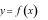 có
có 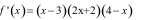 thì có mấy cực trị?
thì có mấy cực trị?
A. 2 B. 1 C. 3 D. 0
Cho hàm số
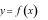 có
đồ thị hàm số
có
đồ thị hàm số 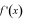 như hình vẽ. Đồ thị hàm số
như hình vẽ. Đồ thị hàm số 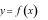 nghịch
có mấy điểm cực trị?
nghịch
có mấy điểm cực trị?
A. 2 B. 1 C. 3 D. 0
Hàm số
 đạt cực tiểu tại
đạt cực tiểu tại 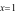 khi:
khi:
A. 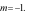 B.
B. 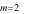 C.
C.  D.
D. 
Tìm giá trị thực của tham số m để hàm số
 đạt cực đại tại
đạt cực đại tại 
A. m = 1 B. m = 2 C. m = -2 D. m = 0











