Cộng đồng chia sẻ tri thức Lib24.vn

Bài 5 trang 146 SGK Giải tích 12

Gửi bởi: Nguyễn Thị Ngọc Vào 15 tháng 5 2019 lúc 15:12:35

Lý thuyết

Câu hỏi

Cho hàm số: \(y = {x^4} + a{x^2} + b.\)

a) Tính \(a,\, b\) để hàm số có cực trị bằng \(\displaystyle{3 \over 2}\) khi \(x = 1.\)

b) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số đã cho khi \(\displaystyle a = {{ - 1} \over 2}, \, \,b = 1.\)

c) Viết phương trình tiếp tuyến của \((C)\) tại các điểm có tung độ bằng \(1.\)

Hướng dẫn giải

Ta có: \(y' = 4{x^3} + 2ax.\)

a) Nếu hàm số có cực trị bằng \(\displaystyle{3 \over 2}\) khi \(x = 1\) thì: ta có đồ thị hàm số đi qua điểm có tọa độ \(\left( {1;\;\dfrac{3}{2}} \right)\) và có \(y'\left( 1 \right) = 0\)

\( \Leftrightarrow \left\{ \matrix{
y'(1) = 0 \hfill \cr 
y(1) = {3 \over 2} \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
4 + 2a = 0 \hfill \cr 
1 + a + b = {3 \over 2} \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{
a = - 2 \hfill \cr 
b = {5 \over 2} \hfill \cr} \right.\)

b) Khi \(\displaystyle a = {{ - 1} \over 2},b = 1\) ta có hàm số: \(\displaystyle y = {x^4} - {1 \over 2}{x^2} + 1\)

- Tập xác định: \((-∞; +∞).\)

- Sự biến thiên: \(y' = 4{x^3} - x = x\left( {4{x^2} - 1} \right).\)

\(\begin{array}{l}
\Rightarrow y' = 0 \Leftrightarrow x\left( {4{x^2} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
4{x^2} - 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \pm \dfrac{1}{2}
\end{array} \right..
\end{array}\)

Trên các khoảng \(\displaystyle ({{ - 1} \over 2};0)\) và \(\displaystyle ({1 \over 2}\; + \infty )\) có \( y’ > 0\) nên hàm số đồng biến.

Trên các khoảng \(\displaystyle ( - \infty ; {{ - 1} \over 2}) \) và \( \displaystyle (0;{1 \over 2})\) có \( y’ < 0\) nên hàm số nghịch biến.

- Cực trị: Hàm số đạt cực đại tại \(x = 0;\;\;{y_{CD}} = 1.\)

Hàm số đạt cực tiểu tại \(\displaystyle x =  \pm {1 \over 2}; \,{y_{CT}} = {{15} \over {16}}.\)

Bảng biến thiên:

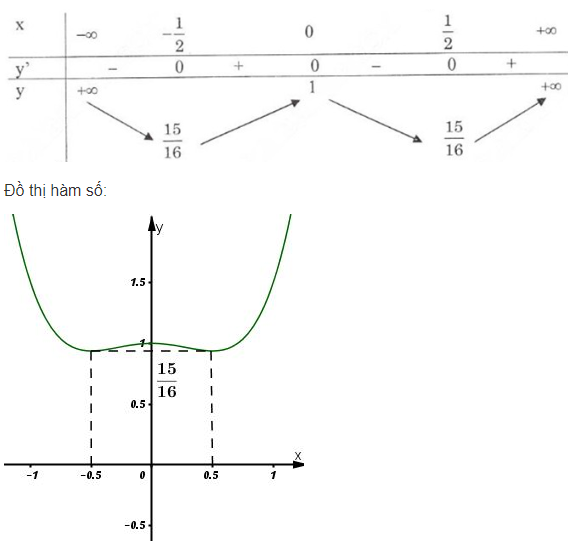
Đồ thị cắt trục tung tại điểm \(y = 1\), không cắt trục hoành.

c) Với \(y = 1\) ta có phương trình:

 \(\displaystyle {x^4} - {1 \over 2}{x^2} = 0 \Leftrightarrow x \in \left\{ {0, \pm {1 \over {\sqrt 2 }}} \right\}\)

Trên đồ thị có 3 điểm với tung độ bằng 1 là:

\(\displaystyle {M_1}({{ - 1} \over {\sqrt 2 }}; \, 1);{M_2}(0; \, 1);{M_3}({1 \over {\sqrt 2 }}; \, 1)\)

Ta có \(y’(0) = 0\) nên tiếp tuyến với đồ thị tại điểm \(M_2\) có phương trình là \(y = 1.\)

Lại có:

\(\displaystyle y'({1 \over {\sqrt 2 }}) = {1 \over {\sqrt 2 }};y'({-1 \over {\sqrt 2 }}) = {{ - 1} \over {\sqrt 2 }}.\)

Tiếp tuyến của đồ thị hàm số tại điểm \({M_1}\left( { - \dfrac{1}{{\sqrt 2 }};\;1} \right)\) là: \(y =  - \dfrac{1}{{\sqrt 2 }}\left( {x + \dfrac{1}{{\sqrt 2 }}} \right) + 1 =  - \dfrac{1}{{\sqrt 2 }}x + \dfrac{1}{2}.\)

Tiếp tuyến của đồ thị hàm số tại điểm \({M_2}\left( {  \dfrac{1}{{\sqrt 2 }};\;1} \right)\) là: \(y = \dfrac{1}{{\sqrt 2 }}\left( {x - \dfrac{1}{{\sqrt 2 }}} \right) + 1 = \dfrac{1}{{\sqrt 2 }}x + \dfrac{1}{2}.\)

Update: 15 tháng 5 2019 lúc 15:12:35

Các câu hỏi cùng bài học

Có thể bạn quan tâm

Học kỹ năng trực tuyến
Doremon chế
Khảo sát trực tuyến